在Arduino DSP系列的第二部分中,我们将继续深入研究数字信号处理的基础知识。我们将学习数字滤波器的特性以及在MATLAB中处理信号时如何应用这些特性。在下一篇文章中,我们将制作一期有关傅里叶变换的深入教程,并研究语音信号最重要的参数:频率。
软件
- Matlab
第1步:如何将信号导入 Matlab
用Audacity录制语音信号后,现在是时候在MATLAB中进行处理了。此功能可以通过 wavread函数完成,该函数负责读取(.wav)声音文件。Audacity的输出信号具有此扩展名。此函数的输入是信号名称(testSound.wav),在MATLAB函数中,您只需要写“testSound”即可。该函数的输出如下所示:
- Y – 信号名称
- Fs – 信号的采样率
- Bits – 位数
我们可以使用以下代码实现此函数。该代码还能够播放声音,让用户在信号处理过程中听到信号如何随时间变化。
[s0,fs,bits] = wavread('testSound');
sound(s0,fs);
pause(9)
t=(0:length(s0)-1)/fs;
figure
plot(t,s0),grid
title('The initial signal.');
xlabel ('tTime')
ylabel('s0(n)');
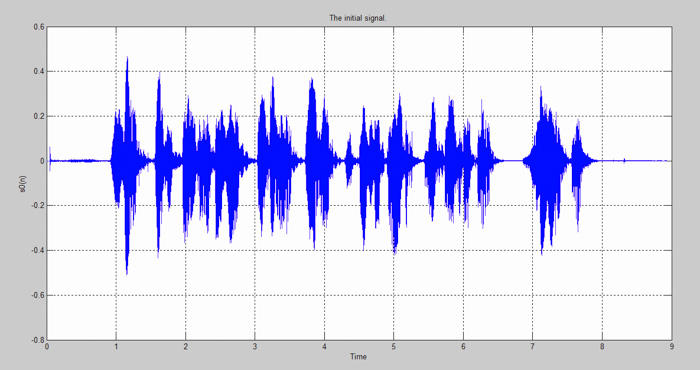
图1:Matlab中的语音信号
如果您想获得人声信号的更多信息,您只需输入音频文件名称(后缀名为.wav),然后函数 audioinfo 就会给您返回声音参数。
audioinfo('testSound.wav')
此函数非常方便,尤其是当一个信号是未知信号时。比如,如果在处理一个信号时无法确定采样率、持续时间和位/样本等必要信息,那么就可以使用上述函数查询该信号的更多信息。
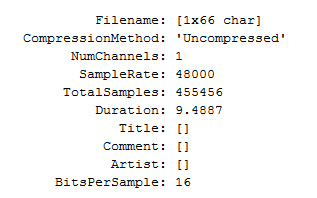
图2:信号属性
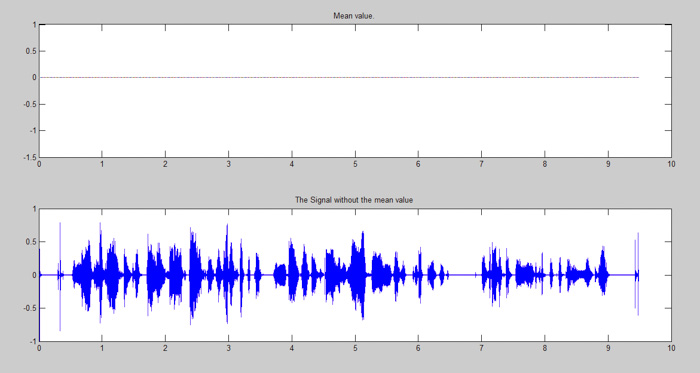
图3:声波及其平均值
第2步:去除平均值(或DC分量)
直流(DC)分量是添加到纯交流(AC)波形(比如语音信号)的恒定电压。纯AC波形的真实平均电压为零。语音信号是模拟信号,但是用Audacity将其转换为数字信号时,会获得一个DC分量。发生这种情况是因为Audacity拥有自己的范围并对信号进行了重新调整。通常,模拟信号范围为-0.5至0.5V。我们需要0.5V的直流分量,这是因为程序使用一系列正数来缩放样本值(每个样本值被转换为从0到N的数字;N是自然数)。
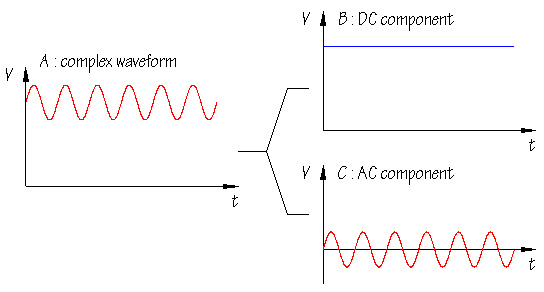
图4:交流分量和直流分量说明
但是,如果存在DC分量,那么AC的幅度会根据DC分量的值发生变化。我们来看一下 图 4。假设您有一个幅度为2V峰-峰值的正弦波,同时叠加了一个0.5V的直流分量,那么最终信号的幅度最高为1.5 V,最低为-0.5 V。
我们应该查看一下信号是否具有直流分量,并且要确定直流分量的值。我们可以通过绘制数值来实现,也可以在命令窗口中输入M实现。
M = mean(s0)
figure
subplot(2,1,1), plot(t,M)
title('Mean value.');
s1 = removeDC(s0);
subplot(2,1,2), plot(t,s1)
title('The Signal without the mean value');
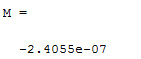
图5:信号平均值
去除平均分量很重要,因为语音信号本身不含直流分量,而我们希望使用纯净的音频波形。 removeDC 函数中的以下代码能够计算信号的平均值并将其从原始信号中除去。
function [sOut] = removeDC(sInput)
DC = mean(sInput);
sOut = sInput - DC;
end
第3步:抽取过程
我们的采样频率现在为48000Hz,我们希望将其变成16000Hz。通过抽取,我们可以降低信号的采样率。抽取可以通过MATLAB中的 decimate 函数实现。当我们对一个语音信号进行采样时,根据奈奎斯特采样定理,最小频率应为8kHz——这是因为人类听觉最大带宽为4kHz。
这样做是因为我们想比较原始信号与抽取信号之间的差异,并了解这种修改如何改变原始信号。
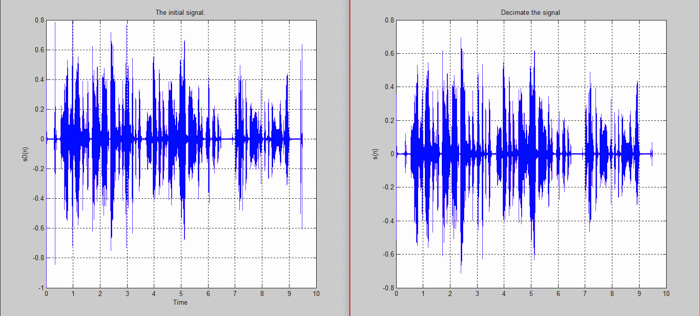
图6:抽取的信号
进行抽取(或下采样)时,我们将采样率修改成较低的速率(与之前的采样率相比)。如下图所示,左侧模拟信号的采样率高于右侧的模拟信号。这意味着我们对采样频率进行抽取。
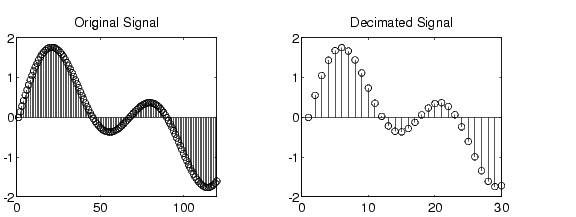
图 7: 抽取的信号
我们还可以进行上采样——下采样的反过程,并增加采样频率。这可以通过插值技术和低通滤波器来完成。
fe2=fs/3;
%s2 = decimate(s1,3);
s2 = decimate(s0,3);
t1=linspace(0,length(s2)/fe2, length(s2));
figure
plot(t1,s2),grid
title('Decimate the signal');
ylabel('s(n)');
sound(s2,fe2);
pause(9)
第4步:信号滤波
简单来讲,数字滤波器是一种离散时间、离散幅度的卷积器。数字滤波器在信号处理中很重要,因为与模拟滤波器相比,它可以处理多个操作。(我们可以假设数字滤波器的成本更高,因为我们需要特殊的数字信号处理器来运行滤波算法的功能。)
每个数字滤波器都有不同的规格:通带、阻带和纹波。我们首先回顾一下以下术语。
- 通带:一个滤波器允许通过的频率带。
- 截止频率:用户选择的某个频率,表示可以通过滤波器的理论频率。为了避免走样,此频率必须低于 采样频率/2 。在电子学中,截止频率是指信号功率变小两倍的频率值。
- 阻带:所有高于此频段的频率都无法通过滤波器。
数字滤波器可以分为两类:FIR(有限脉冲响应),滤波器系数为整数。IIR(无限脉冲响应),具有模拟等效模型,并且阶数较低时更有效。
FIR/IIR滤波器最重要的特性之一是相位特性:
- FIR: 线性相位特性
- IIR:非线性相位特性(或相位失真)
FIR滤波器属性 – dspGuru by Iowegian International
“线性相位是指滤波器的相位响应是频率的线性(直线)函数(不包括+/-180度的相位缠绕)。这使得通过滤波器的所有频率的延迟都相同。因此,这种滤波器不会引起“相位失真”或“延迟失真”。在某些系统中,比如在数字数据调制解调器中,没有相位/延迟失是FIR滤波器相对于IIR和模拟滤波器的关键优势。”
MATLAB中有众多类型的数字滤波器可供选择,但是我们需要了解如何将其应用于我们的具体场景。对于本项目,我们选用IIR滤波器,因为它更有效,即与FIR滤波器相比,我们需要更小的阶数。

图 8: IIR 滤波器
以下代码可以在MATLAB中创建一个Butterworth滤波器。添加滤波器阶数和截止频率后,此函数会返回滤波器系数。
fn = fe2/2;
fc=3400; % cutoff frequency
[Bd,Ad] = butter(40,3400/fn,'low');
在命令行中输入 help butter ,就可以通过MATLAB帮助了解为什么采样率会除以2。“[b,a] = butter(n,Wn)会返回一个n阶低通数字Butterworth滤波器的传递函数系数以及归一化截止频率Wn”,且“截止频率Wn必须满足0.0 < Wn < 1.0,1.0对应于采样率的一半。”
滤波器系数存储在 Bd 和 Ad 变量中。
数字滤波器术语 – dspGuru by by Iowegian International
滤波器系数 – 与数字滤波器结构内的延迟信号采样值相乘的常数集。数字滤波器设计就是要确定产生所需滤波器频率响应的滤波器系数。对于FIR滤波器,根据定义,滤波器系数就是滤波器的脉冲响应。
滤波器阶数 – 上述每种滤波器都有一个阶数(N)特征;N阶是指实现滤波器所需无功元件的数量。对于IIR滤波器,滤波器阶数等于滤波器结构中的延迟元件数。通常,滤波器阶数越大,滤波器的频率幅度响应性能越好。
此滤波器的另一个重要方面是频率响应——滤波器如何影响频谱分量。滤波器的理想频率响应应该是一个完整的矩形,其幅度为1,截止频率为0.5。在现实生活中,您可以根据自己的应用场景选择滤波器类型。
一个数字滤波器的频率响应如下图所示。在我们的例子中,通带的幅度平坦,没有纹波。截止频率为3400Hz,这意味着我们的信号通过了一个低通滤波器,其频率不会超过此限值。如图所示,截止频率后面没有阻带,这就是为什么可能有其他频率比它高的原因。这可以通过增加滤波器的阶数来改善。
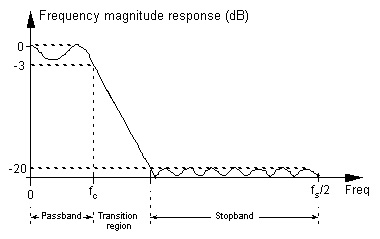
图 9: 滤波器的频率响应
如图10所示,椭圆滤波器在截止频率处的幅频曲线下降最陡,但振幅不稳定。切比雪夫1和2在通带和阻带中有幅度波动。Butterworth滤波器在这两个频段上都没有幅度波动,因此我们在应用中采用了这种滤波器;然而,这种滤波器的缺点是其过渡带较大。
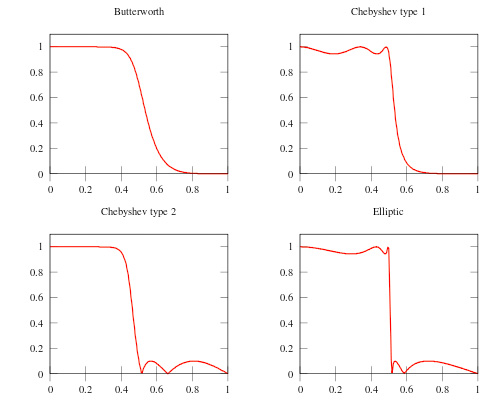
图 10: IIR 滤波器类型
IIR滤波器的阶数小于FIR滤波器的阶数。
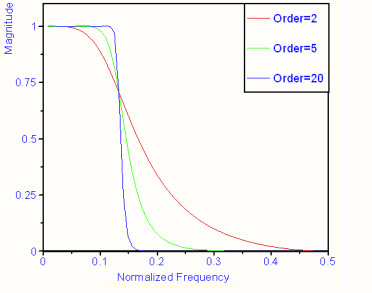
图 11: 不同阶数的Butterworth滤波器
在本文应用中,我们将滤波器的阶数设为40,以使频率响应尽可能地接近理想频率响应。如图11所示,随着滤波器阶数的增加,性能在频率响应方面也会提高。
对信号进行滤波和抽取之后,我们需要观察原始信号与变换信号之间的差异。我们使用绘图功能并生成一个音频信号。
验证结果是否有效的最简单方法就是查看这些信号。我们来比较一下原始信号(48kHz采样率)和最终信号(16kHz采样率)。最终信号没有太大的噪音,这是一件非常好的事情。

图 12: 原始信号与经过滤波的信号之间的差异
在第2部分中,我们的目标是学习数字滤波器的特性并用MATLAB进行测试。到目前为止,我们已经设法了解了采样率的含义以及采样率的变化如何影响音频信号。在下一篇文章中,我们将从另一个角度——利用傅里叶变换(即频域)——处理音频信号。