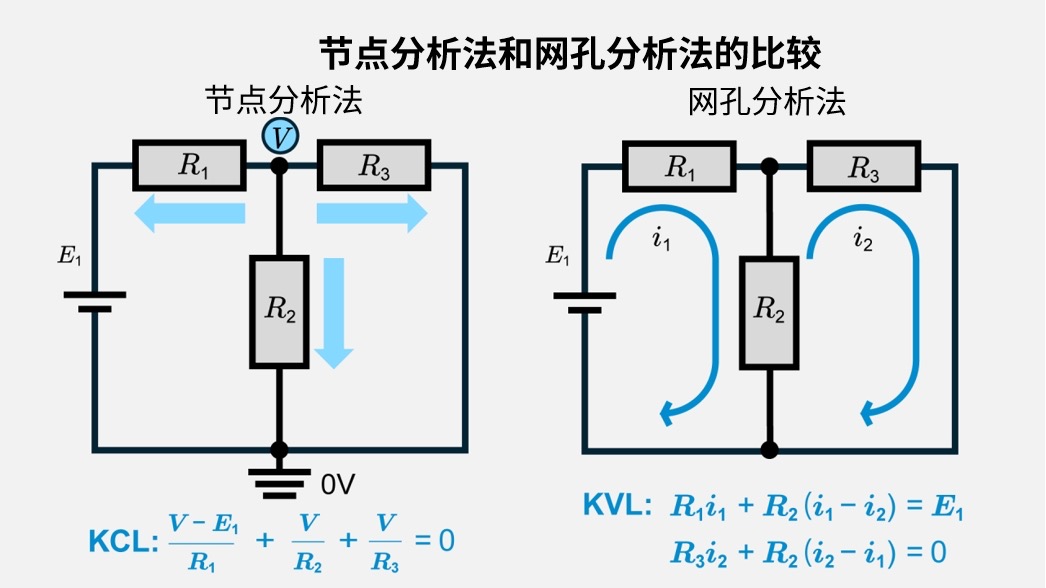
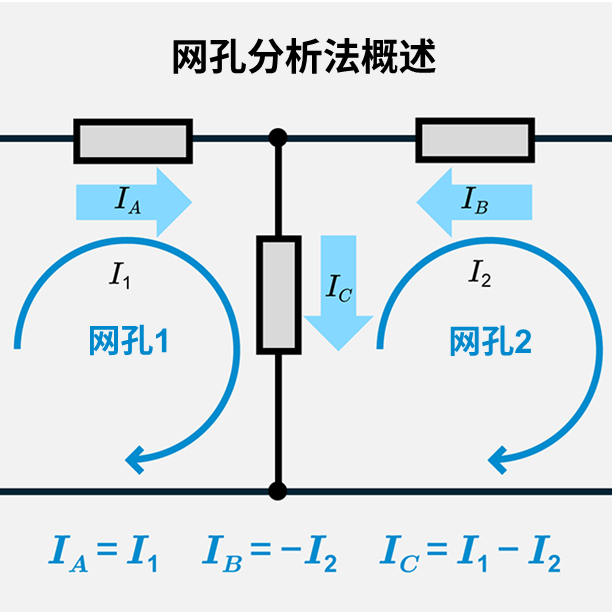
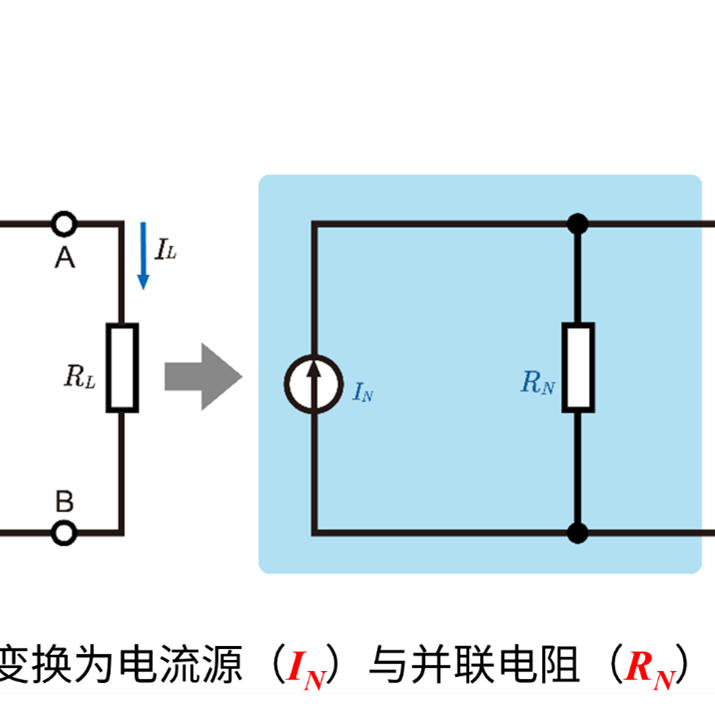
\(\)

什么是Δ-Y变换（Y-Δ变换）

Δ-Y变换（或Y-Δ变换）是一种可以简化包括三相电路在内的复杂电阻和阻抗网络，并实现顺畅分析的基础技术。顾名思义，通过三角形（德尔塔，Δ）接法与星形（Y）接法的等效互换，使得Δ-Y变换（或Y-Δ变换）能够更简单地进行串并联组合及电压电流计算。

三相交流电主要广泛应用于工业设备和商用设备领域，根据负载侧电路采用Δ接法或Y接法的不同，其电压和电流的处理方式存在显著差异。掌握Δ-Y变换（Y-Δ变换）的基础知识，对于在负载设计和故障排查中“轻松把握端子间的等效电阻”、“梳理不平衡负载”等需求大有裨益。

Δ-Y变换（Y-Δ变换）基础

节点标注和典型电路图

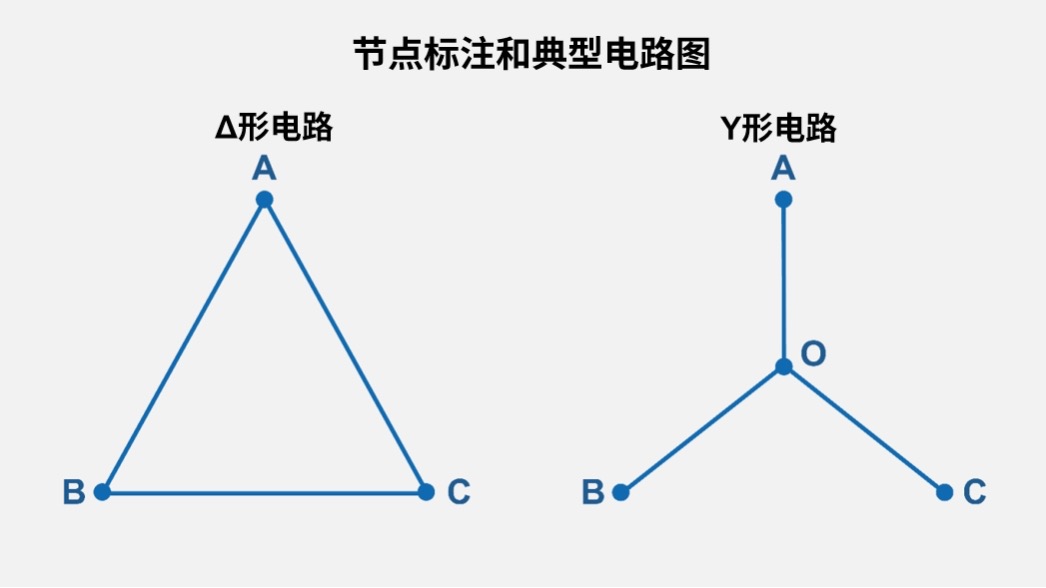
• 典型标注示例
  • 大多情况下，三角形（Δ形电路）的顶点标注为A、B、C。这是因为按字母顺序排列会便于理解且不易混淆。
• 节点数量的差异
  • Δ形电路由A–B–C共3个节点构成。
  • Y形电路除A-B-C外还包括中心节点O，由4个节点构成。
  • 有时也会采用连接至一个节点（如接地等）的绘制方法。

Δ形电路和Y形电路的结构

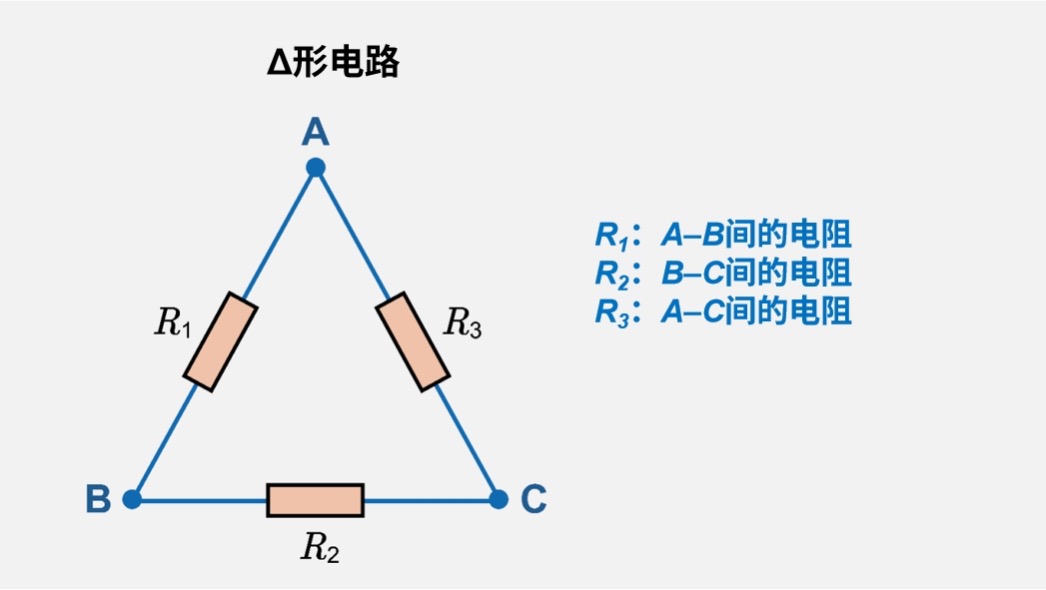
• Δ形电路（Delta电路）
  设三个端子分别为A、B、C，各边（\(R_1\)：A–B、\(R_2\)：B–C、\(R_3\)：C–A）上存在电阻或阻抗，构成三角形电路。

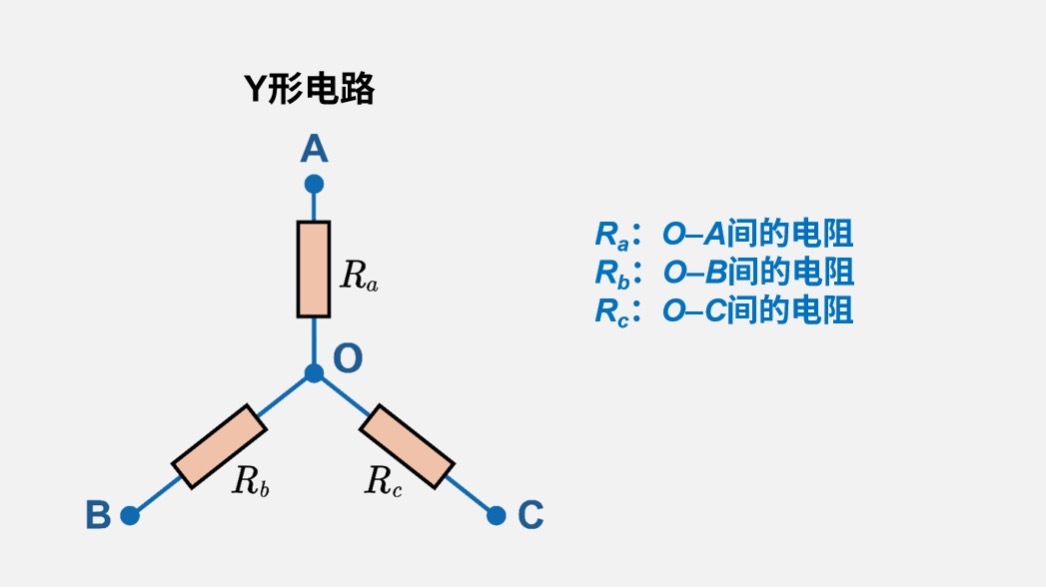
• Y形电路（星形电路）
  设一个中心点O，从中心点分别向端子A、B、C延伸支路（\(R_a\)：O-A、\(R_b\)：O-B、\(R_c\)：O-C），形成星形结构。

无论是哪种结构，都经常涉及到三相负载和电阻网络分析。

• 注意事项
  • 如果将电阻\(R_1\)定义为A-B之间的元件，那么也需要在电路图中将\(R_1\)WE置于A-B之间，以确保文档与图纸的一致性。
  • 即使将电路旋转或翻转，只要节点连接未被破坏，仍视为等效电路。
  • 由于节点会随电路方向发生变化，因此节点间的最终连接是否正确至关重要。

Δ→Y变换与Y→Δ变换的基本公式

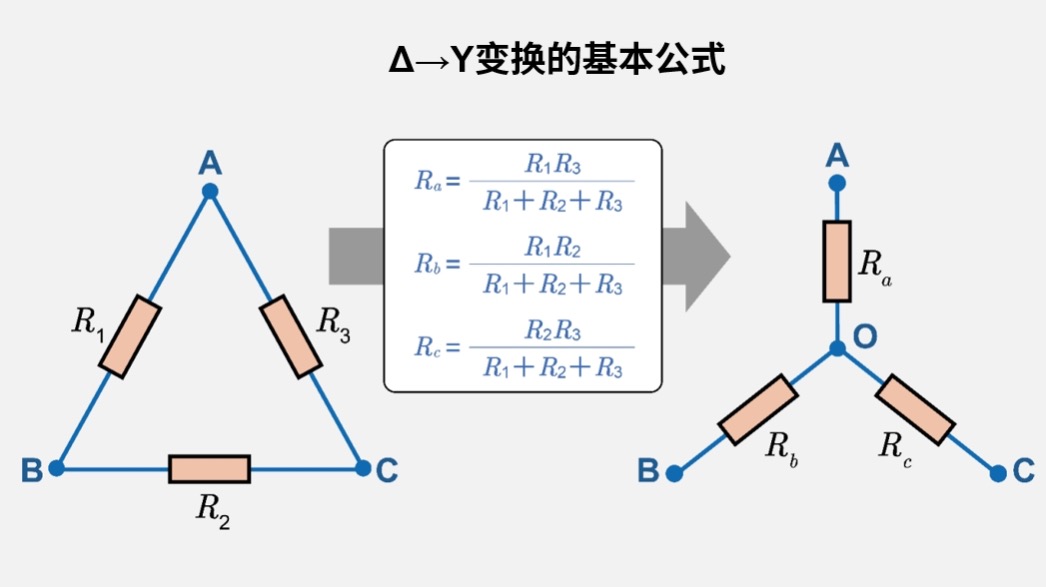
• ΔΔ→Y变换
  \(R_a=\displaystyle\frac{R_1 R_3}{R_1+R_2+R_3}, R_b=\displaystyle\frac{R_1 R_2}{R_1+R_2+R_3}, R_c=\displaystyle\frac{R_2 R_3}{R_1+R_2+R_3}\)

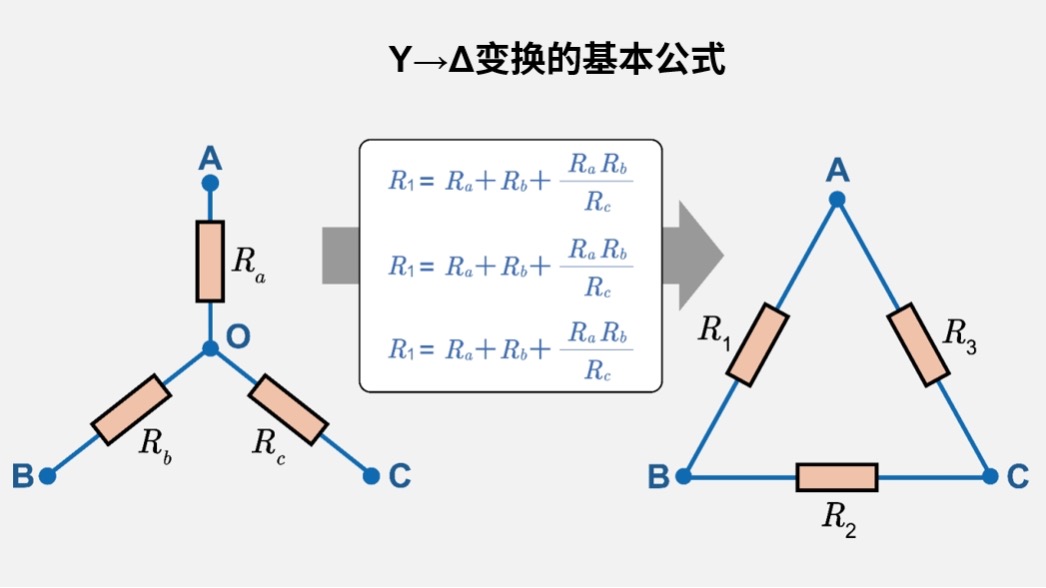
• Y→Δ变换
  \(R_1=R_a+R_b+\displaystyle\frac{R_a R_b}{R_c} , R_2=R_b+R_c+\displaystyle\frac{R_b R_c}{R_a} , R_3=R_c+R_a+\displaystyle\frac{R_c R_a}{R_b}\)

这些公式可根据“变换前后端子A-B、B-C、C-A各自的等效电阻保持相同”的条件推导得出。关键在于，即使使用阻抗替代电阻，其形式依然保持不变。

通过具体实例了解Δ-Y变换（Y-Δ变换）

Δ→Y变换示例

设Δ形电路的电阻为

\(R_1=30Ω, R_2=60Ω, R_3=90Ω\)

那么

\(R_a=\displaystyle\frac{R_1 R_3}{R_1+R_2+R_3}=\displaystyle\frac{30×90}{180}=15Ω,\)

\(R_b=\displaystyle\frac{R_1 R_2}{R_1+R_2+R_3}=\displaystyle\frac{30×60}{180}=10Ω,\)

\(R_c=\displaystyle\frac{R_2 R_3}{R_1+R_2+R_3}=\displaystyle\frac{60×90}{180}=30Ω\)

因此，Y形电路中的各电阻值为（R_a、R_b、R_c）=（15Ω、10Ω、30Ω）。

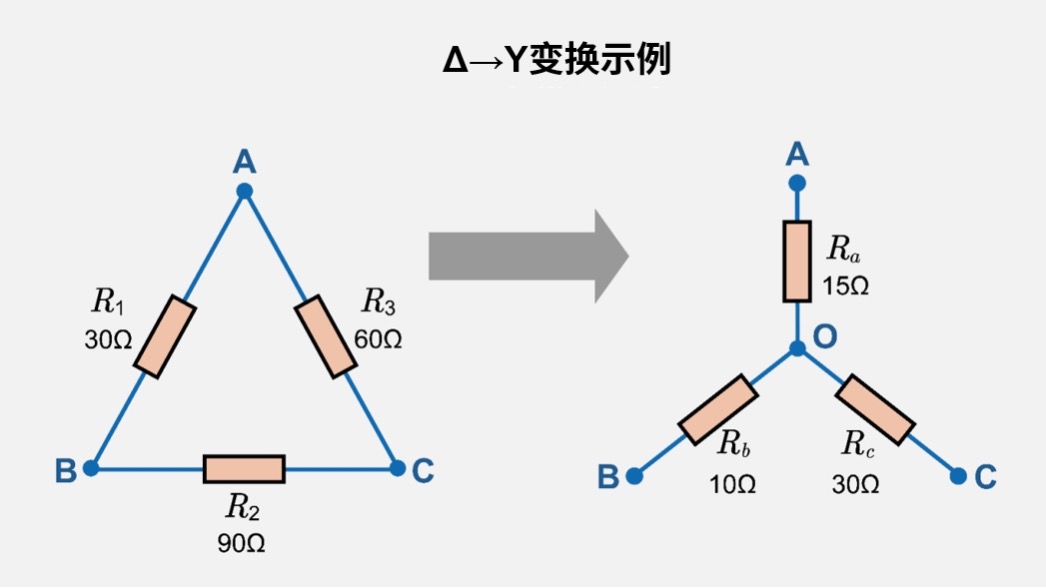
Y→Δ变换示例

设Y形电路的电阻为

\(R_a=5Ω, R_b=10Ω, R_c=20Ω\)

那么

\(R_1=5+10+\displaystyle\frac{5×10}{20}=17.5Ω, R_2=10+20+\displaystyle\frac{10×20}{5}=70Ω,\)

\(R_3=20+5+\displaystyle\frac{20×5}{10}=35Ω\)

因此，Δ形电路中的各电阻值为（R₁、R₂、R₃）=（17.5Ω、70Ω、35Ω）。

Δ-Y变换（Y-Δ变换）公式推导过程

Δ-Y变换中串联电阻和并联电阻的识别

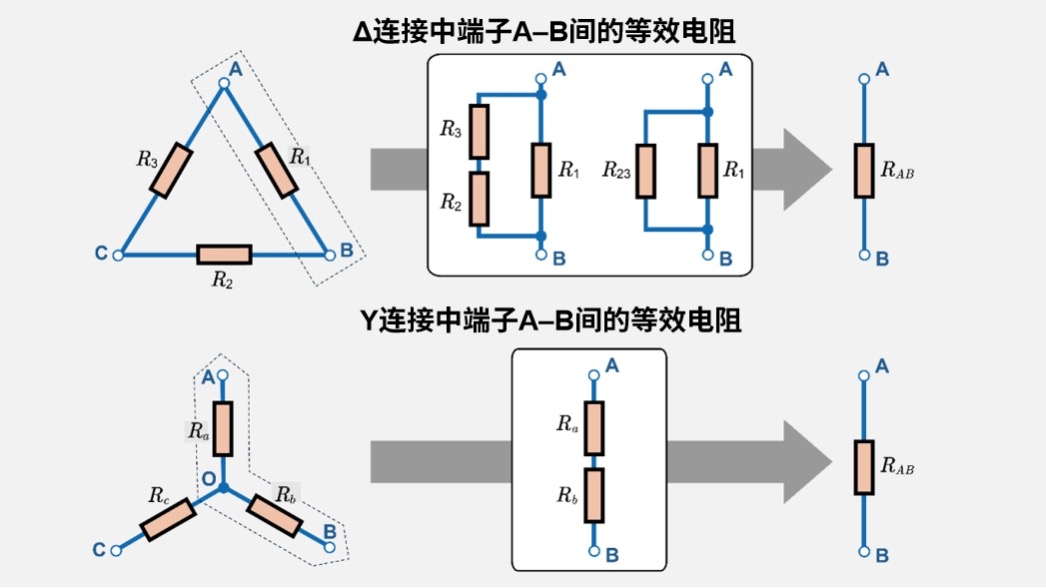
1. 串联电阻（Series Combination）
   • 当两个电阻共享仅一个节点，而另一端分别与不同节点连接时，可视为串联关系。
   • 串联关系下的合成电阻\(R_{series}\)=\(R_a\)+\(R_b\)
   • 例如，在Δ形电路中观察A–B之间，呈现\(R_2\)与\(R_3\)串联、\(R_1\)与它们并联的关系。
2. 并联电阻（Parallel Combination）
   • 若两个电阻共享两端，则为并联关系。
   • 合成电阻为1/\(R_{parallel}\)=1/\(R_a\)+1/\(R_b\)
   • 关于前面提到的A-B之间，则是\(R_2\)+\(R_3\)串联→\(R_1\)与其并联的连接关系，这是两者的基本的区分。
3. 重温欧姆定律（Ohm’s Law）
   • \(V\)=\(I\)×\(R\)是电阻电路的基本公式。
   • 利用串联电路中电流处处相等、并联电路中电压处处相等的特性，即可求出Δ-Y变换的基础——等效电阻。
4. 由单一电阻（single resistor）替代
   • 通过反复进行串联和并联计算，最终可将“端子间的电阻”整合为一个阻值。
   • Δ-Y变换可以说是一种在三相电路中系统化实现这种等效电阻转换的技术。

从Δ到Y的变换公式推导

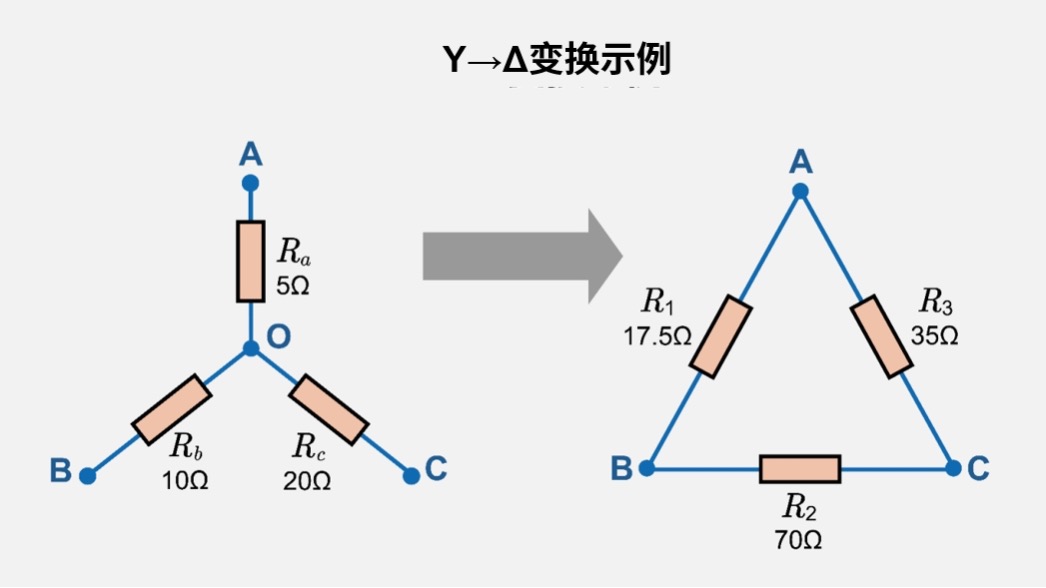
实际推导过程需建立“使Δ形电路侧、Y形电路侧的A-B间等效电阻一致“、“B-C间、C-A间同理”这三个方程。

下面将更详细地推导将三角形接法的电阻（\(R_1\)、\(R_2\)、\(R_3\)）转换为星形接法（\(R_a\)、\(R_b\)、\(R_c\)）的转换公式。设三角形电路的顶点为A、B、C，各边的电阻分别为\(R_1\)（A–B）、\(R_2\)（B–C）、\(R_3\)（C–A）。另外，在转换目标星形电路中，设从中心点O到A的电阻为\(R_a\)，从O到B的电阻为\(R-b\)，从O到C的电阻为\(R_c\)。转换的基本方针是施加“端子A-B、B-C、C-A之间所见的等效电阻在Δ形电路和Y形电路中均相同”这一条件。

1. Δ形电路中A–B间等效电阻
   设端子A-B间所见的等效电阻为\(R_{AB}\)。由于\(R_2\)和\(R_3\)为串联连接，故将该电阻记为\(R_{23}\)。\(R_{AB}\)是\(R_1\)和\(R_{23}\)的并联连接。
   \(R_{23} =R_2+R_3\)
   \(R_{AB} = \displaystyle\frac{R_1 R_{23}}{R_1+R_{23}} = \displaystyle\frac{R_1 (R_2+R_3)}{R_1+(R_2+R_3)} = \displaystyle\frac{R_1 R_2+R_3 R_1}{R_1+R_2+R_3}\)
2. Y形电路中A-B间等效电阻
   设端子A-B间所见的等效电阻为\(R_{AB}\)。由于\(R_a\)和\(R_b\)为串联连接，所以得到如下公式：
   \(R_{AB} = R_a+R_b\)
   通过运用基尔霍夫定律（KVL、KCL）建立联立方程求解A-B间的等效电阻，最终会得到一个条件方程：“（端子A-B间的等效电阻）=（Δ形电路侧的A-B间等效电阻）”。
   \(R_a+R_b=\displaystyle\frac{R_1 R_2+R_3 R_1}{R_1+R_2+R_3}\)
3. 端子B–C间、C–A间亦同法操作
   端子B–C间、C–A间也按照同样的步骤，通过建立并求解三个联立方程，使Δ形电路与Y形电路各端子间的等效电阻一致。
   \(R_b+R_c=\displaystyle\frac{R_1 R_2+R_2 R_3}{R_1+R_2+R_3}\)
   \(R_c+R_a=\displaystyle\frac{R_3 R_1+R_2 R_3}{R_1+R_2+R_3}\)
4. \(R_a\)、\(R_b\)、\(R_c\)的求解
   将A-B间、B-C间、C-A间的等效电阻分别相加：
   \(2(R_a+R_b+R_c) = \displaystyle\frac{2(R_1 R_2+R_2 R_3+R_3 R_1)}{R_1+R_2+R_3}\)
   \(R_a+R_b+R_c=\displaystyle\frac{R_1 R_2+R_2 R_3+R_3 R_1}{R_1+R_2+R_3}\)
   要求得\(R_a\)，可推导出如下基本公式。同样可以计算出\(R_b\)和\(R_c\)。
   \(R_a=\displaystyle\frac{R_1 R_2+R_2 R_3+R_3 R_1}{R_1+R_2+R_3}-(R_b+R_c)\)
   \(= \displaystyle\frac{R_1 R_2+R_2 R_3+R_3 R_1}{R_1+R_2+R_3} – \left(\displaystyle\frac{R_1 R_2+R_2 R_3}{R_1+R_2+R_3}\right) = \displaystyle\frac{R_1 R_3}{R_1+R_2+R_3}\)

从Y到Δ的变换公式推导

从Y到Δ的转换与从Δ到Y的转换遵循相同的原则。将Y形电路的\(R_a\)、\(R_b\)、\(R_c\)转换为Δ形电路的\(R_1\)、\(R_2\)、\(R_3\)时，需建立使端子A-B间、B-C间、C-A间的等效电阻相等的条件。

基于基尔霍夫定律建立联立方程，求解端子A-B间、B-C间及C-A间的电阻。

Δ-Y变换（Y-Δ变换）的应用

在实际的电路分析中，Δ-Y（或Y-Δ）变换在电阻网络无法通过串联或并联组合简化时尤为实用。这种情况常见于桥接网络、不平衡三相负载，或两个节点间无直接连接电阻的复杂黑箱部分。通过在合适的点应用Δ-Y变换，工程师能够将复杂的拓扑简化为更简单的形式，从而便于运用欧姆定律和基尔霍夫定律等传统方法计算电流、电压或功率。即使是在可以使用仿真工具的情况下，这种变换方法仍是设计评审和故障分析时解读电路行为、进行电路简化的重要手段。

对平衡负载和不平衡负载应用Δ-Y变换（Y-Δ变换）

当三相电路中的负载电阻（或阻抗）像\(R_1\)=\(R_2\)=\(R_3\)一样完全相等时，称为“平衡负载”。此时，无论是Δ连接还是Y连接，分析都相对简单，但在实际的系统中，往往会出现一定程度的不平衡。

• 不平衡负载状态下，各相的电阻或电抗不同，可能导致线电流和相电压出现不平衡现象。
• 通过Δ-Y变换适当整合这种电路，便于量化不平衡程度，有利于在故障排查中发现电路设计缺陷和电流偏移等问题。

阻抗（复数）的Δ-Y变换（Y-Δ变换）

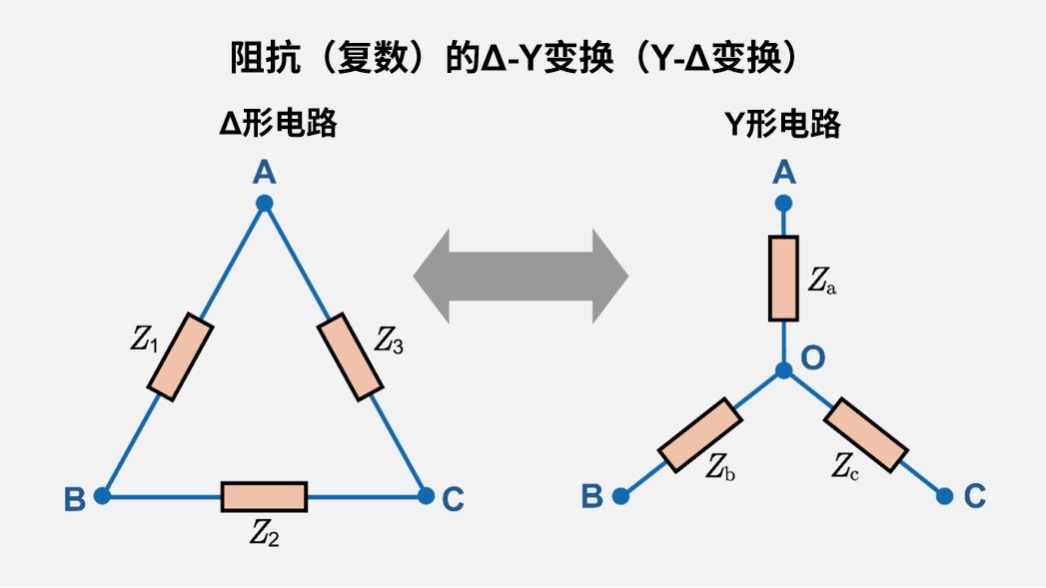
Δ-Y变换同样适用于将电阻\(R\)替换为包含电感和电容的阻抗\(Z\)=\(R\)+\({jX}\)。

\(Z_a=\displaystyle\frac{Z_1 Z_3}{Z_1+Z_2+Z_3},…\)

三相交流电路中实际上往往包含电感和电容的电抗，采用复数表示方式可分析相位差乃至无功功率。

Δ-Y变换（Y-Δ变换）在三相交流电路中的应用

线电压和相电压的关系梳理

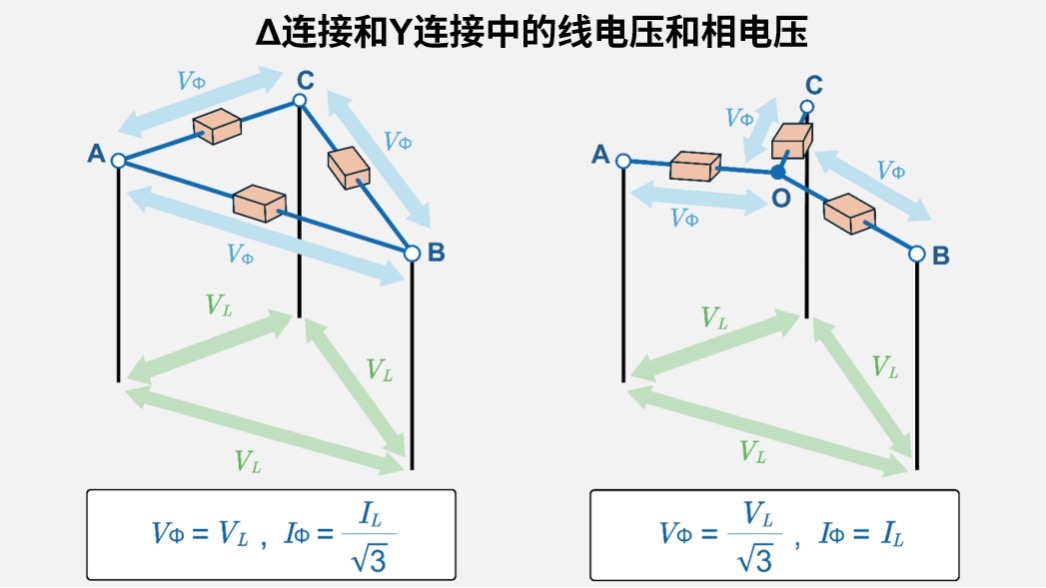
在三相交流电路中，连接方式不同使得相电压和线电压之间的关系也不同。

• Δ接法中，各电阻直接连接线电压\(V_L\)：
  \(V_ϕ=V_L\)
• Y接法中，施加于各电阻（阻抗）的电压为相电压\(V_ϕ\)，与线电压\(V_L\)的关系为：
  \(V_ϕ=\displaystyle\frac{V_L}{√3}\)

相电流与线电流的对应关系也不同。

• Δ接法：
  \(I_ϕ=\displaystyle\frac{I_L}{√3}\)
• Y接法：
  \(I_ϕ=I_L\)

由于Δ形接法和Y形接法的电压、电流大小关系不同，因此即使负载相同，接法不同也会使电源侧的电流值发生变化。通过深入了解相关的三相交流基础知识，将会使Δ-Y变换的意义更加明晰。

与星-三角启动和三相变压器的关联

• 星-三角启动
  多数三相电机采用“仅启动时采用Y形连接，稳态运行时切换为Δ形连接”的方案。其设计目的在于通过降低启动时的相电压来抑制大电流，当电机开始旋转后切换至全电压驱动（Δ连接），从而实现高效率运转。
  这部分内容虽然与Δ-Y变换公式本身不同，但要想正确了解“Y连接时和Δ连接时，端子间的电压和电流如何变化”，Δ-Y关系作为基础知识非常重要。
• 三相变压器
  通过对绕组进行Δ-Δ、Y-Y或Δ-Y等不同方式的连接，可调整线电压与相电压的变换比值。在变压器接线中，Δ-Y变换的思路具有实际应用价值，有助于了解“Δ形和Y形的区别”。

（参考）多电源电路与叠加定理

应用叠加定理对含多个独立电源的电路进行分析时，通过将电路简化为“仅保留一个电源，其余电源短路或开路“的形式，最终再将各简化电路的分析结果进行叠加。

• 与Δ-Y变换联用：
  • 当电源较多使得电路很复杂时，可先禁用部分电源将电路简化，在此基础上进行Δ-Y变换，将更易于进行电阻/阻抗的合成。
  • 通过将“各电源单独作用时的电流、电压”结果相加，最终可掌握多电源同时作用时的情况。
• 实际应用时的注意事项：
  • 在直流电源和交流电源共存的电路中，相位和平均值等参数的处理有时会比较复杂。在三相交流电路中存在相位差（120°）或谐波分量时，需要结合复数和傅里叶分析方法进行处理。

关于叠加定理的详细介绍，请参阅“什么是叠加定理”一文。

总结

1. Δ-Y变换（Y-Δ变换）是三相电路及电阻网络的基础技术
   • 通过将三角形连接（Δ）的三个电阻（阻抗）转换为星形连接（Y），或相反的转换，可在保持端子间等效电阻的同时简化电路。
2. 其公式无论对电阻（R）还是阻抗（Z）均可通过相同的形式适用
   • 在三相交流电路中，由于经常出现电抗，通常采用复数表示方式。可将公式中的\(R\)直接改为\(Z\)。
3. 无论对平衡负载还是不平衡负载，皆可轻松应用
   • 在三相交流电路中，区分使用线电压\(V_L\)和相电压\(V_ϕ\)，对于负载不平衡时的故障分析至关重要。
4. 在实际应用中，与电机的星-三角启动和三相变压器接线方式的关联很重要
   • 启动时Y形连接、稳态运行时切换为Δ形连接的三相电机，正是巧妙运用Δ-Y电路的电压电流差异的典型范例。
5. 与其他电路分析方法（如叠加定理）结合适用，其作用更大
   • 通过梳理多电源的影响，并运用Δ-Y变换简化部分电路，可使复杂的系统分析变得更加顺畅。

当企业的技术人员在进行电源设计或设备维修等涉及三相交流电的作业时，若已经掌握Δ-Y变换的基础知识，分析效率将会显著提高。无论是平衡负载还是不平衡负载，均可准确捕捉电路端子间的等效变换关系。