目录
阻抗(Z)是表示交流(AC)电路中电流流动难易程度的值。它是以电阻(R)和电抗(X)组合而成的复数形式来表示的。电阻器、电容器、电感器等元件相互影响,电抗随频率的变化而变化。例如,电容器的电抗随频率的升高而降低,而电感器的电抗则随频率的升高而增加。另外,阻抗还需考虑电压与电流之间产生的相位差。因此,阻抗对于实现高质量的信号传输和提高能源利用效率而言非常重要,特别是阻抗匹配,是尽可能减少信号丢失、提升设备性能所不可或缺的技术。
本文将围绕“什么是阻抗?”“阻抗匹配”等主题,详细介绍从阻抗的基本概念到实际应用相关的内容。
阻抗的基本概念
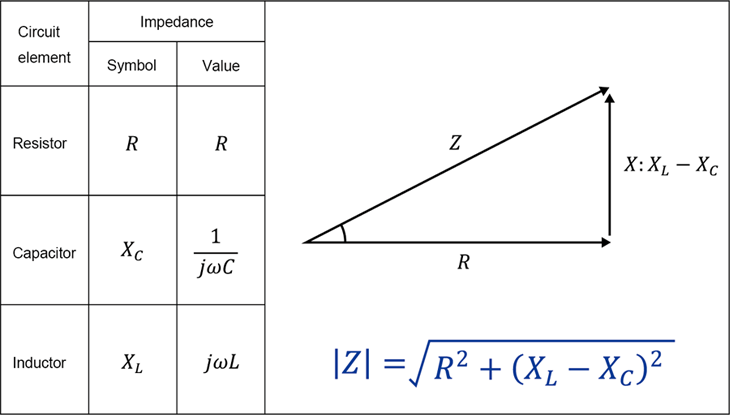
阻抗是电路中的一个重要概念,综合表示元器件和电路对交流信号的阻碍作用。阻抗值越高,电流越难流过,因此阻抗值可以显示出电流在交流电路中流动的难易程度。阻抗的符号为“\(Z\)”,单位与在直流电路中时相同,为“\(Ω\)(欧姆)”。
阻抗概述
阻抗既包括在输出电压的电路中的输出阻抗,也包括在输入电压的电路中的输入阻抗。阻抗值可以通过电压和电流之比求得。由于阻抗的计算方法因电路结构而异,因此,针对想要求得的阻抗值,需要注意计算方法是否适当。阻抗是交流电路中电压与电流的比值,最初是源自电路学的术语,另外还适用于与音频有关的声、光、电磁波等,有声阻抗、光阻、(电磁)波阻抗等各种阻抗。
阻抗、电阻和电抗之间的关系
当提到“电流流动时受到的阻碍程度”时,很多人可能会将其与电阻联系起来。那么,阻抗和电阻之间究竟有什么区别呢?
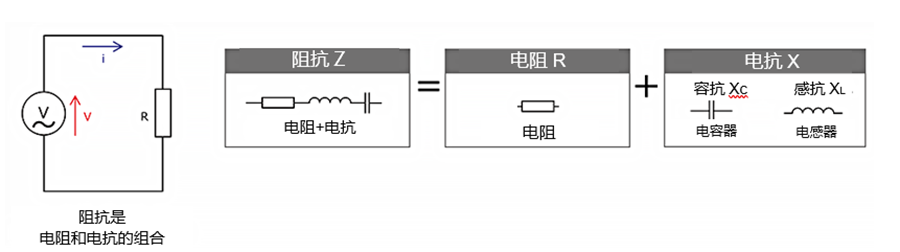
电阻是阻抗的组成要素之一。电阻的特点是其值只考虑电阻器,而且其值不会随频率的变化而变化。而受频率影响的被称为“电抗”,电抗包括“容抗”和“感抗”两种。电抗的符号为“\(X\)”、单位为“\(Ω\)”。电抗与电阻的组合就是阻抗。可见,阻抗不仅包括单纯的电阻,还包括依赖于频率的电感(线圈特性)和电容(电容器特性)产生的电抗。
阻抗的重要性
了解阻抗为什么如此重要,对于有效设计电路和故障排除而言至关重要。适当的阻抗匹配可以更大程度地抑制信号反射,并有助于优化功率传输。
阻抗单位
阻抗由电路中电阻和电抗组成,其单位用欧姆(\(Ω\))表示。电阻表示直流电路中对电流流动的阻碍作用,而阻抗则表示交流电路中的总电阻。
阻抗符号
阻抗通常用大写的“\(Z\)”来表示。
在数学上,阻抗通过复数表示,实部表示电阻(\(R\)),虚部表示电抗(\(X\))。
其表达式如下:
\(Z=R+{j}X\)
这里的\(j\)是虚数单位,\(j^2=-1\)。
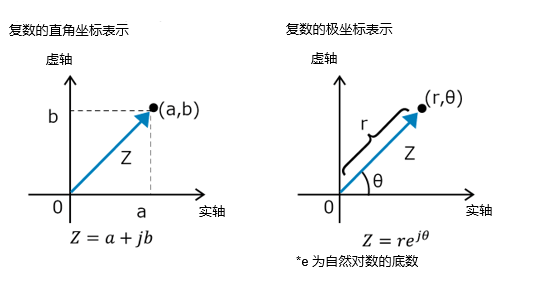
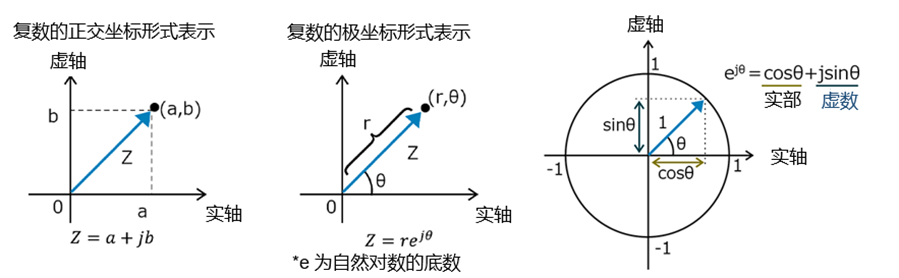
阻抗的复数表示
由于阻抗是以复数的形式表示的,所以具有幅值和相位角。幅值与电阻有关,则相位角则与电抗有关。通过以极坐标的形式表示复数,有助于理解这些信息。
\(Z = |Z| × e^{j\theta}\)
这里的∣\(Z\)∣表示阻抗的幅值(阻抗模),\(θ\)表示相位角。
阻抗和电抗之间的区别
下面介绍对于理解阻抗而言很重要的“电抗”。希望大家能够通过介绍了解阻抗与电抗之间的区别和关系。
什么是电抗
电抗是交流电路中阻碍电流流动的因素,会受到频率的影响。电抗包括容抗和感抗两种。电抗的符号为“\(X\)”,单位为“\(Ω\)”。
容抗
容抗是电容器(Capacitor)对电流的阻力。电容器是用来蓄电和放电的电子元件,被广泛应用于智能手机、电脑和电视等各种电子设备。电抗的符号为“\(X\)”,容抗用符号“\(X_C\)”来表示,单位与电抗一样,也是“\(Ω\)”。
容抗由以下公式表示:
\(X_C = \displaystyle \frac{1}{\omega C}\)
ω为角频率,用
\(\omega = 2\pi f\)
来表示,代入后得到如下公式:来表示,代入后得到如下公式:
\(X_C = \displaystyle \frac{1}{2\pi fC}\)
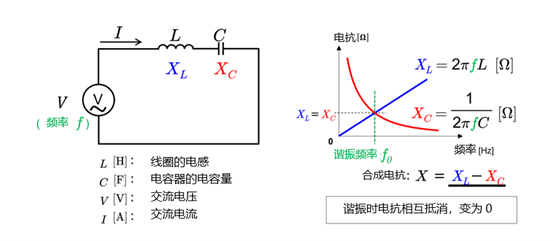
f表示信号的频率,C表示电容器的容量。从公式可以看出,容抗具有其值随频率的增加而减小的特点。
感抗
感抗是线圈(电感器)对电流的阻力。线圈是作用于电和磁的电子元件,与电阻器和电容器等元件同样被广泛用于各种电子设备。感抗的符号为“\(X_L\)”,单位为“\(Ω\)”。
感抗由下列公式表示:
\(X_L = \omega L\)
与容抗一样,当代入角频率后,公式会变为:
\(X_L = 2\pi fL\)
\(L\)是线圈的电感值。与容抗相反,感抗具有其值随频率的提高而增加的特点。
阻抗与电抗之间的关系
正如在电阻部分所介绍的,阻抗是电阻和电抗的组合。请记住:电抗是阻抗的组成要素之一。由于电抗又分为容抗和感抗,所以也可以说阻抗由电阻、容抗和感抗这三部分组成。
阻抗的复数表示对于了解交流信号的详细情况来说非常重要。复数形式的阻抗(\(Z\))表示如下:
\(Z = R + j\omega L – j(\displaystyle \frac{1}{\omega C})\)
其中\(R\)是电阻,\(L\)是电感,\(C\)是电容,\(ω\)是角频率。
阻抗的计算
计算阻抗的基本公式
阻抗的基本公式
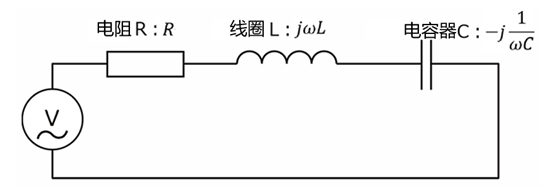
阻抗由电阻(\(R\))、电感(\(L\))和电容(\(C\))组成,以复数的形式表示。
阻抗(\(Z\))的基本公式如下:
\(Z = R + jX\)
\(= R + j(X_L + X_C)\)
\(= R + j(\omega L – \displaystyle \frac{1}{\omega C})\)
其中\(R\)是电阻,\(L\)是电感,\(C\)是电容,\(j\)是虚数单位,\(ω\)是角频率。
复数表示
基于这些基础计算,以复数表示的阻抗Z可用下列公式表示:
\(Z = |Z| × e^{j\theta}\)
其中|\(Z\)|是幅值,\(θ\)是相位角。
通过理解这些基本公式,即可计算复杂电路的阻抗,并详细掌握电路的特性。
例题:阻抗的计算
下面我们通过具体的例子来了解阻抗计算的思路。在以下条件下计算阻抗:
- 电阻(\(R\)):50\(Ω\)
- 电感(\(L\)):0.1\(H\)
- 电容(\(C\)):100\(μF\)
- 角频率(\(ω\)):100\(rad/s\)
首先,将这些值代入基本公式进行计算:
\(Z = 50 + j(100 \times 0.1 – \displaystyle \frac{1}{100 \times 0.001})\)
该计算结果表示整个电路的阻抗。
阻抗和电路元素
RLC串联电路是电阻(\(R\))、电感(\(L\))和电容(\(C\))串联形成的电路。
该电路的阻抗(\(Z\))由这些元素组成,并随频率的变化而变化。
阻抗的基本公式:
RLC串联电路的阻抗由下列公式表示:
\(Z = R + j(\omega L – \displaystyle \frac{1}{\omega C})\)
其中\(j\)是虚数单位,\(ω\)是角频率。该公式由电阻分量和电抗分量组成,随频率的变化而变化。
与角频率的关系
角频率通常用乘以\(2\pi\)的值来表示。即\(\omega = 2\pi f\) ,其中f是频率。
谐振条件
在RLC串联电路中,当电抗相互抵消时会发生谐振。
也就是当\(ωL=1/ωC\)时发生谐振。
阻抗的复数表示
RLC串联电路的阻抗用复数来表示,用极坐标形式表示如下:
\(Z_{\text{total}} = re^{j\theta} = \sqrt{R^2 + (\omega L – \displaystyle \frac{1}{\omega C})^2} (\sin(\theta) + j\cos(\theta))\)
其中θ是相位角。
RLC并联形成的阻抗(\(Z\))表示由电阻(\(R\))、电感(\(L\))和电容(\(C\))组成的电路的复阻抗。如果要求出并联电路的总阻抗,就需要取每个组件的阻抗的倒数,将它们相加,然后求出该总和的倒数:
\( \displaystyle \frac{1}{Z} = \displaystyle \frac{1}{R} + \displaystyle \frac{1}{j\omega L} + j\omega C = \displaystyle \frac{1}{R} + \displaystyle \frac{-j}{\omega L} + j\omega C \)
为了将它们构成复数,需要使用公分母\(RωL\):
\( \displaystyle \frac{1}{Z} = \displaystyle \frac{\omega L + jR – jR\omega^2 LC}{R\omega L} = \displaystyle \frac{\omega L + j(R – \omega^2 LC)}{R\omega L} \)
接下来,将分子和分母化简:
\( Z = \displaystyle \frac{R\omega L}{\omega L + j(R – \omega^2 LC)} = \displaystyle \frac{R\omega L(\omega L – j(R – \omega^2 LC))}{(\omega L)^2 + (R – \omega^2 LC)^2} \)
将公式展开并进一步整理分母和分子,得到如下阻抗:
\( Z = \displaystyle \frac{\omega^2 L^2 R}{R^2 (1 – \omega^2 LC)^2 + \omega^2 L^2} + j \displaystyle \frac{\omega L R^2 (1 – \omega^2 LC)}{R^2 (1 – \omega^2 LC)^2 + \omega^2 L^2} \)
通过执行该计算的各个步骤,就可以准确求出并联RLC电路的阻抗。要求出阻抗的大小(|\(Z\)|),需要计算出该复数的绝对值。具体而言,是先分别求出实部和虚部的平方值,将它们相加,然后求其平方根:
\( |Z| = \sqrt{\left( \displaystyle \frac{R\omega^2 L^2}{R^2 (1 – \omega^2 LC)^2 + \omega^2 L^2} \right)^2 + \left( \displaystyle \frac{\omega L R^2 (1 – \omega^2 LC)}{R^2 (1 – \omega^2 LC)^2 + \omega^2 L^2} \right)^2 } \)
通过计算,即可求出并联RLC电路的阻抗大小(|\(Z\)|)。再将公式变形后,可简化如下:
\( |Z| = \displaystyle \frac{\omega RL}{\sqrt{R^2 (1 – \omega^2 LC)^2 + \omega^2 L^2}} \)
各电路元素(电阻、电感、电容)的阻抗特性对于理解电流和电压等信号在通过电路时如何受到影响来说是非常重要的。
电阻的阻抗
电阻(\(R\))的阻抗与频率无关。阻抗(\(Z_R\))是指单纯的电阻值本身。
\(Z_R = R\)
电感的阻抗
电感(\(L\))的阻抗与频率成正比。阻抗(\(Z_L\))由下列公式表示:
\(Z_L = jX_L = j\omega L\)
其中\(j\)是虚数单位,\(ω\)是角频率。
电容的阻抗
电容(\(C\))的阻抗与频率成反比。阻抗(\(Z_C\))由下列公式表示:
\(Z_C = \displaystyle \frac{1}{j\omega C}\)
阻抗的相位角
各元素的阻抗以复数形式表示,并有相位角。例如,对于电容而言,其相位角(\(θ_C\))为\(-\pi/2\)。
各电路元素的总阻抗
当这些元素串联或并联连接时,其总阻抗是每一个元素的阻抗之和。例如,在RLC串联电路中,即电阻、电感和电容的阻抗相加。
\(Z_{\text{total}} = Z_R + Z_L + Z_C\)
电流与电压的相位差
在RLC串联电路中,电阻(\(R\))、电感(\(L\))和电容(\(C\))的阻抗均用复数表示,导致电流(\(I\))和电压(\(V\))之间产生相位差。该相位差因各元素的阻抗的相对大小而异。
阻抗与电流的相位差
当电路中不仅含有电阻,还含有电感和电容时,电流和电压之间会产生相位差。该相位差取决于以复数形式表示的阻抗(\(Z\))。
\(V = I × Z\)
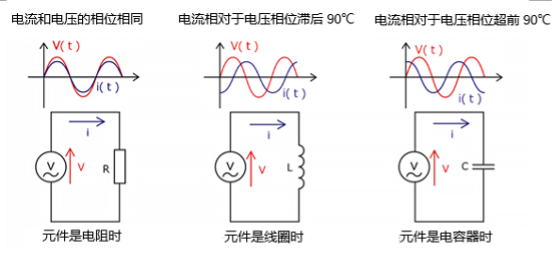
电流与电压之间的相位差因电路元素的种类而异。这会产生被称为“相移”的现象,即电感导致电流滞后、而电容导致电流超前、波形随时间变化而偏移的现象。当发生相移时,波形的波峰(峰值)会随时间而变化,可以显示出电路中的信号随时间滞后或超前了多少。
| Resistive Circuit | Inductive circuit | Capacitive circuit |
|---|---|---|
| \(V_L = I \times X_R = RI\) | \(V_L = I \times X_L = j(\omega L)I\) | \(V_C = I \times X_C = -j\left(\displaystyle \displaystyle \frac{1}{\omega C}\right)I\) |
| Voltage and current are in phase | Current delays by 90° | Current forwards by 90° |
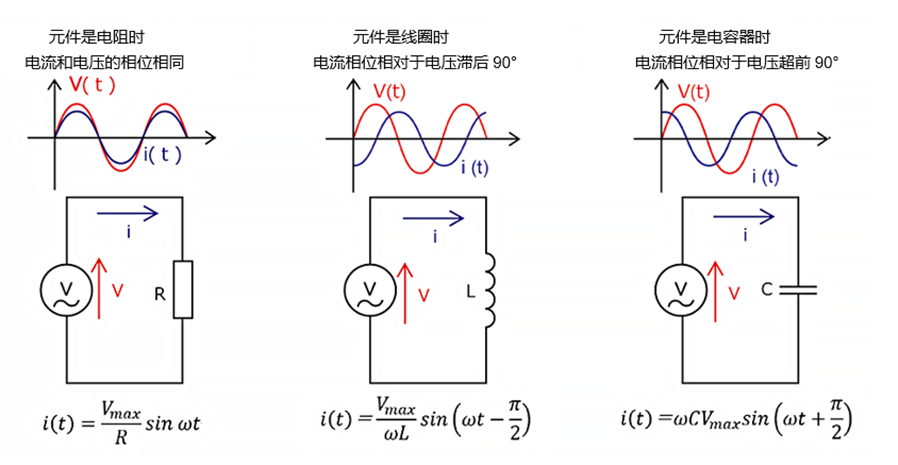
交流电路中的电压和电流
在交流电路中,电流和电压都会随时间变化。在交流电路中也适用欧姆定律,但使用的是“阻抗”而不是“电阻”。
\(V(t) = I(t) × Z(t)\)
其中,\(V(t)\)和\(I(t)\)是随时间变化的电压和电流,\(Z(t)\)是随时间变化的阻抗。
高级的阻抗概念
阻抗匹配的重要性
阻抗匹配是一种通过适当调整电路和系统中各元素的阻抗来提高信号传输和能量传输效率的技术。阻抗匹配,可以更大程度地抑制信号反射和丢失,优化系统性能。

阻抗匹配的基础知识
阻抗匹配是指使信号源和负载的阻抗相同。这可实现有效的信号传输并更大程度地抑制信号反射。基本目标是确保所传输的信号以最大功率到达负载端。
\(Z_{\text{out}} (Z_{\text{source}}) = Z_{\text{in}} (Z_{\text{load}})\)
其中\(Z{\text{out}}(Z_{\text{source}})是信号源的阻抗,Z_{\text{in}} (Z_{\text{load}})\)是负载的阻抗。
\(I = \displaystyle \frac{V}{Z_{\text{in}} + Z_{\text{out}}}\)
其中总电压为V,流经电路的电流为I。根据欧姆定律可以得出:
\(V_{in} = I \times Z_{in} = Z_{in} \times \displaystyle \frac{V}{Z_{in} + Z_{out}}\)
其中负载\(Z_{\text{in}}\)两端的电压为\(V_{\text{in}}\)。根据\(P_{\text{in}}=V_{\text{in}}×I\),这里消耗的功率为:
\(P_{\text{in}} = Z_{\text{in}} \left( \displaystyle \frac{V}{Z_{\text{in}} + Z_{\text{out}}} \right) \left( \displaystyle \frac{V}{Z_{\text{in}} + Z_{\text{out}}} \right) = V^2 \displaystyle \frac{Z_{\text{in}}}{(Z_{\text{in}} + Z_{\text{out}})^2}\)
当\(Z_{\text{in}}=Z_{\text{out}}\)时,\(P_{\text{in}}\)最大。
阻抗匹配的优点
优化信号传输:
阻抗匹配可使信号在传输路径中以最佳条件传输,并更大程度地减少信号丢失。
防止信号反射:
如果阻抗不匹配,信号就会被反射,效率就会降低。通过阻抗匹配,可以将信号反射抑制在最低。
优化功率传输:
当阻抗匹配时,功率传输会得到优化,能源会得到有效利用。
输入阻抗和输出阻抗是指信号进入和离开电路时的阻抗,它们之间的区别在于输入阻抗表示信号源侧的性质,输出阻抗表示负载侧的性质。
当输入阻抗不适合信号源时,部分信号就会被反射,从而造成传输信号丢失。同样,当输出阻抗不适合负载时,也会发生同样的问题。
输入阻抗
输入阻抗是指电路或设备输入侧的阻抗。该阻抗是接收信号源信号的电路侧或设备的电阻、电抗和电感之和。
当输入阻抗设计得当并与信号源的输出阻抗相匹配时,来自信号源的信号将以最大效率被传输至输入电路。适当的输入阻抗可以将信号丢失降至最低,并高效地传输来自信号源的信号。
输入阻抗匹配示例:
音频放大器的输入阻抗需要与音频源(CD播放器或麦克风等)的输出阻抗相匹配。
输出阻抗
输出阻抗是指电路或设备输出侧的阻抗。该阻抗是电路或设备向外部提供信号时的电阻、电抗和电感之和。当输出阻抗设计得当并与负载的输入阻抗相匹配时,信号将以最大效率被传输至外部。适当的输出阻抗可将信号反射降至最低,防止信号丢失。当输出阻抗与负载不匹配时,可能会发生信号反射并造成信号丢失。
输出阻抗匹配示例:
扬声器的输出阻抗需要与放大器的输入阻抗相匹配。
高级的阻抗计算和应用
复杂电路结构中的阻抗计算
一般的阻抗计算公式适用于简单的电路结构,但在复杂的电路中以及频率响应非常重要的情况下,就需要更高级的阻抗计算了。这包括使用数值分析和方针工具。
阻抗的应用
高级阻抗计算适用于高频电路、通信系统和RF(射频)电路的设计等领域。这些领域要求精细的阻抗匹配,以将信号丢失降至最低并实现高效的能量传输。下面通过几个示例来介绍这类高级阻抗匹配方法。
优化S参数:
S参数(Scattering Parameters)是表示传输路径和电路特性的指标,在高级阻抗匹配中被用来寻找最适合的值。通过使用优化算法,使S参数最小化或最大化等调整,来实现特定频率下的阻抗匹配。
阻抗匹配变压器:
使用变压器是实现特定频段下的阻抗匹配的方法之一。作为高级的设计方法,有时会使用非对称变压器或各频段特性不同的变压器。这种方法可在很宽的频率范围内进行有效的阻抗匹配。
使用隔离式转换器:
在进行高级阻抗匹配时,可以在信号源和负载之间配置隔离式转换器。隔离式转换器可以转换信号并进行阻抗匹配。这可使信号被有效传输并减轻电路之间的阻抗失配问题。
自适应控制匹配:
一种使用自适应控制算法来实时调整阻抗匹配的方法。控制算法可以根据频率和环境的变化情况优化阻抗,以保持最佳的通信效率。
优化微带线设计:
在高频电路中,优化微带线的设计可影响阻抗匹配。通过优化带状线尺寸和材料特性,可以在频段内实现有效的阻抗匹配。
阻抗的测量
“阻抗测量”是指向电子设备或电路等施加电压使电流流动并测量电阻值的过程。下面将为您介绍在哪些应用中需要经常用到阻抗测量,以及进行阻抗测量时应该注意的关键要点。
阻抗测量的目的
阻抗测量是评估和了解电路及系统中元素的阻抗特性的重要方法。其目的是优化各元素的阻抗,以提高信号的传输效率。通过测量阻抗,可以更大程度地抑制信号反射和丢失,提升系统性能。
电路设计和优化:
阻抗测量被用于评估电路中各元素的实际阻抗。这能够使电路设计者准确把握电路特性,并根据需要优化设计。例如,为了提高带宽利用率和信号传输效率,会要求对各元素的阻抗进行优化调整。
滤波器设计:
为了使信号通过特定的频段,需要适当的滤波器设计。阻抗测量用来评估滤波器电路中各元素的阻抗,并实现所需的频率特性。
天线设计:
天线需要有适当的阻抗匹配才能在特定频段内有效地收发信号。阻抗测量在天线设计和优化中发挥着重要作用。
阻抗匹配:
要在不同的电路和器件之间有效地传输信号,就需要进行阻抗匹配。通过阻抗测量,可以准确地把握输入和输出阻抗,并找到合适的方法来实现匹配。
故障检测:
当电路和器件的阻抗与正常阻抗不同时,意味着可能有故障或问题。阻抗测量可以检测故障和异常,对于维护保养作业和故障排除非常有用。
阻抗测量的注意事项
阻抗值会因测量方法和测量时的环境而异,如果所使用的测量方法不正确,就无法获得稳定的值。阻抗测量需要施加大范围的稳定正弦波,也就是说,确保“稳定的频率”这一点非常重要。此外,如果存在连接线接触不良或鳄鱼夹生锈等不稳定因素,也会产生杂散电容,并给测量值造成影响。测量时的温度和探头负载等外部因素也会影响到测量值,因此很重要的一点是在整个测量过程中要具备稳定的环境。
事先了解正确测量阻抗的方法是非常重要的,比如需要掌握影响阻抗的因素有哪些、需要计算在稳定环境下多次测量结果的平均值等。
频率的选择:
阻抗依赖于频率,因此需要考虑测量时使用的频率。需要选择与对象器件和电路的特性相符的频率,并调整测量范围和分辨率。要注意的是,如果频率不同,阻抗值也会发生变化。
测量电路的影响:
测量电路本身可能会影响被测对象的阻抗。尤其是在高频条件下,线缆和探头的阻抗可能会变得很大,大到无法忽视的程度。鉴于这些影响,需要确认测量时的电路和探头连接是稳定的,还需要提前校准所使用的测量仪器,这非常重要。
测量信号的幅值:
如果测量信号的幅值过大,就会产生非线性效应而很难准确测量。所以需要选择适当的信号幅值,以在线性范围内测量对象器件。
控制测量环境:
测量环境中的外部电磁噪声和振动可能会影响到测量结果。可以通过采用适当的屏蔽和隔离措施,将外部影响降到最低。
测量时间:
阻抗可能会根据频率、随着时间而变化。要想确保测量稳定性,需要设置合适的测量时间,并保证足够的稳定时间。
被测对象发热量的影响:
当使用大功率时或在高频下测量时,对象本身的发热量可能会影响到阻抗。在测量前,需要考虑到被测对象的热特性,并采取适当的冷却措施。
阻抗的测量方法
准确测量阻抗对于获取可靠的数据而言是必不可少的条件。下面是测量阻抗的基本方法。
信号源的选择:
阻抗测量需要合适的信号源。通常使用交流信号。信号源的频率需要根据对象的特性进行选择。典型频率在数百赫兹到数兆赫兹的范围。
构建测量电路:
要测量阻抗,就需要构建合适的测量电路。测量电路因对象的特性和测量目的而异。典型的电路有串联电路和并联电路。
使用LCR测试仪:
LCR 测试仪(用来测量电感、电容和电阻的装置)广泛用于阻抗的测量。可以使用该测量仪来测量对象在各频率下的阻抗,获得电阻分量、电感分量和电容分量。
扫频:
由于对象的阻抗依赖于频率,所以边改变频率边测量是很有效的方式。通过扫频,可以详细把握对象的频率响应特性。
使用示波器:
可以使用示波器来观测阻抗的动态变化。示波器能够可视化显示信号波形,适合很高频段的测量。
傅里叶变换:
为了准确理解阻抗的频率响应特性,可以对获得的数据进行傅里叶变换。这会使频域中的阻抗结构一目了然。
LCR测试仪是在阻抗测量中非常有用的仪器,尤其适用于测量电阻(Resistance)、电感(Inductance)和电容(Capacitance)。
下面是LCR测试仪基本使用方法的详细指南。
- 确认连接:
首先,将测量对象与LCR测试仪正确连接。通常连接3个或4个端子。被测对 象是表面贴装器件时,需要正确放置探头,这一点非常重要。 - 选择测量模式:
LCR测试仪具有单独测量电阻、电感和电容等各元素的模式。根据被测对象的种类,选择正确的测量模式。 - 设置频率:
由于阻抗依赖于频率,因此需要设置要测量的频率。一般情况下,根据被测对象的特性来选择频率。通常从低频到高频进行测量。 - 设置信号电平:
设置适合被测对象的信号电平。通常从小信号电平开始,然后根据需要增减。过大的信号可能会影响测量结果。 - 自动和手动测量:
LCR测试仪有自动测量模式和手动测量模式。在自动模式下,测试仪会选择最佳设置。在手动模式下,由用户手动设置测量参数。 - 读取结果:
LCR测试仪完成测量后,会显示结果。测量结果中不仅包括电阻、电感和电容值,还可能包括相位差和品质因数等。 - 实施补偿:
在测量线缆较长或测量环境较复杂的情况下,可通过实施补偿来确保测量的准确性。补偿通常在测试仪的设置菜单中进行设置。
通过这些步骤,即可使用LCR测试仪进行准确的、可靠性高的阻抗测量。
音频设备的阻抗
阻抗在音频设备中的重要性
阻抗的作用和影响
对于音频设备而言,在确保可靠的声学性能和设备间的正确连接方面,阻抗的作用非常重要。在电路中,阻抗对交流信号有阻碍作用;在音频设备中,阻抗影响着扬声器、耳机、放大器等各种产品和器件的特性。如果没有准确的阻抗匹配,可能会发生信号丢失和不当的电流,从而影响音质和设备的效率。
对音频设备的具体影响
音质变差:
如果阻抗不匹配,音质可能会变差。例如,当耳机或扬声器的阻抗与放大器不匹配时,会导致信号失真、信号的频率响应发生变化等问题,从而无法获得清晰、平衡的音效。
效率降低:
如果放大器和扬声器等设备没有正确匹配,其效率就会降低,需要更多的功率才能获得相同的音量。这会浪费电力,还可能缩短设备的使用寿命。
作为对策使用的阻抗匹配:
准确的阻抗匹配对于音频设备的设计和运用而言至关重要。设备之间的正确匹配可实现最佳的功率传输,从而有助于提高音质和设备的效率。
阻抗匹配示例
要使信号在音频设备之间平稳地传输,必须进行阻抗匹配。例如,当音源设备和放大器之间的阻抗匹配不当时,就会发生信号衰减或失真,导致音质变差。
耳机和放大器匹配示例:
在耳机和放大器组合中,耳机的阻抗应该与放大器匹配。这样可以实现最大功率传输,并产生清晰、低失真的音效。
阻抗匹配的公式如下:
\(P = \displaystyle \frac{V^2}{Z}\)
其中\(P\)表示功率,\(V\)表示电压,\(Z\)表示阻抗。
当耳机的阻抗为32Ω时,理想情况下,对应的放大器的输出阻抗也应为32Ω。
这样就可以更大程度地进行功率传输,并获得最佳的音质。
正确理解阻抗并在工作中运用
如今,市场上精密的阻抗测量仪器多种多样,已在涉及到电路的企业中被广为应用。虽然使用阻抗测量仪器可以轻松测得阻抗值,但正确理解阻抗对于获得准确的测量值来说是必不可少的前提。因此,在理解阻抗时,加深其与电阻、电抗等概念之间的区别和关系的理解非常重要。
如果不能获取准确的阻抗值,就无法正确地推断电子元器件等产品的内部状态,从而引发判断错误等问题,比如本来存在异常却推断为正常、本来没有异常却被推断有异常。因此,不仅要理解阻抗,还要关注造成测量值偏差的因素。
特别是由于连接线和环境噪声容易造成测量值偏差,所以在测量过程中确保稳定的环境是非常重要的。在工作中,理解这些内容并将其付诸实践,将能够实现可靠性高的阻抗测量,而这非常有利于出色地完成电路品质管理和故障排除工作。