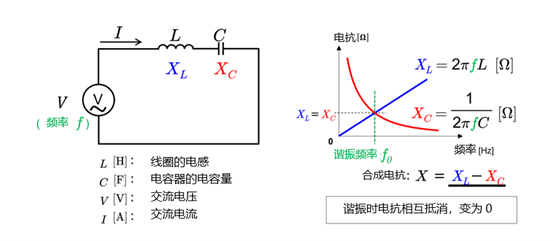
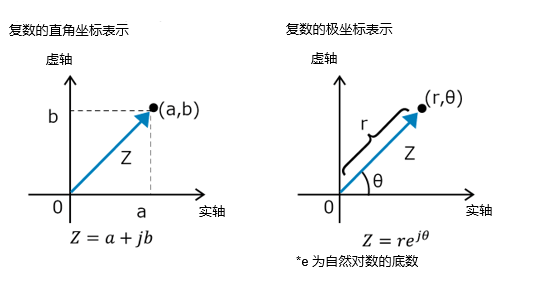
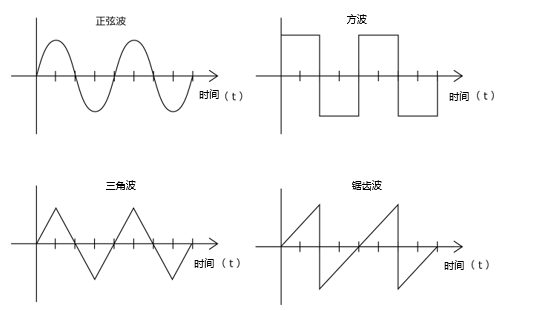
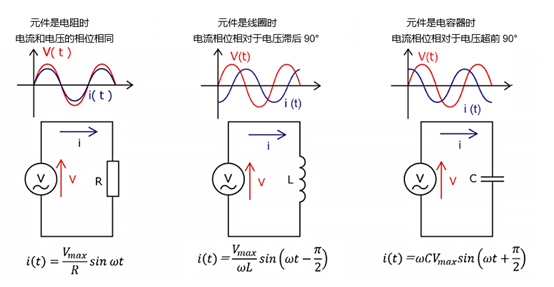
功率因数是电源电路使用有功功率的效率指标,用从0到1的值来表示。其值越接近1,功率因数越高,意味着功率的使用效率越好。交流电功率与功率因数密切相关,如果功率因数低,那么功率波动和损耗就有可能增加。因此,改善功率因数有助于提高电力系统的效率并降低成本。
本文将聚焦“功率因数”,深入探讨其基本概念、实用计算方法以及提高能效的具体手法。
功率因数的定义
功率因数是用来衡量电路效率的指标,用有功功率与视在功率之比来表示。功率因数的取值范围通常是0到1,越接近1,表示效率越高。在直流电路中,功率因数始终为1;在交流电路中,由于线圈和电容的影响,功率因数会发生变化。
如果将其比作啤酒杯,那么啤酒的液体部分就相当于有功功率,表示实际可以使用的能量,这种能量负责驱动电机或设备。泡沫部分相当于无功功率,是无法饮用的多余能量,但会包含在杯子的总容量(视在功率)中。无功功率主要来自线圈和电容等的有源负载,虽然不消耗能量本身,但会增加电力系统的负载。
啤酒的液体部分与杯子整体容量的比值表示功率因数。功率因数越接近1,也就是杯子里的啤酒越多,泡沫越少,表示能量的使用效率越高。相反,如果功率因数较低,也就是泡沫(无功功率)增多,就意味着系统效率降低,产生了功率损耗。减少这种泡沫部分是提高电力系统效率和降低成本的关键要点。

功率因数公式
功率因数是电力系统中的重要指标,用来表示电路效率。准确地说,功率因数为有功功率与视在功率之比,公式如下:
\(功率因数 (PF) = \displaystyle \frac{P(有功功率)[W]}{S(视在功率)[VA]}\)
另外,根据视在功率、有功功率、无功功率之间的关系,也可以用下列公式表示:
\(功率因数(PF)=\displaystyle \frac{P(有功功率)}{\sqrt{(P(有功功率))^2+(Q(无功功率))^2}}\)
通常在0到1之间取值。其值越接近 1,表示功率的使用效率越高。
功率因数的计算
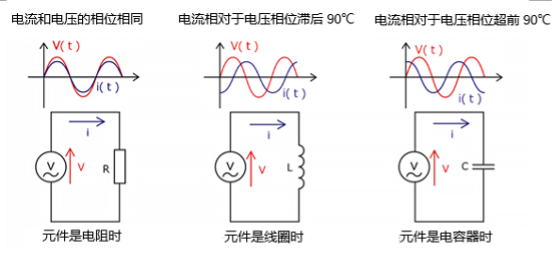
在直流电路(纯电阻电路)中,电流波形和电压波形彼此同相,因此相位差为0度。因此,功率因数如下:
\(PF=cos0°=1\)
也就是说,消耗的瓦数等于消耗的伏安数,功率因数为1。另外,如果在受线圈或电容影响的电路中相位差为90度,则功率因数为:
\(PF=cos90°=0\)
也就是说,消耗的瓦数为零,但有供给无功负载的电压和电流。
功率因数计算示例
例如,某设备的有功功率为500W,视在功率为600VA,则功率因数可计算如下:
\(PF = \displaystyle \frac{500}{600} \ = 0.833\)
根据该公式可以计算出功率因数。
下面我们来看一个更具体的例子。
将电感为0.1H、电阻为50Ω的线圈与100V 50Hz的电源相连接。计算这种情况下线圈的阻抗、电流、功率因数和视在功耗。

线圈的阻抗 \(Z\) 按下列公式计算:
\(Z=\sqrt{R^2+(X_L-X_C)^2}\)
其中,\(R\) 表示电阻,\(X_L\) 表示电感引起的电抗,\(X_C\) 表示电容引起的电抗。
\(X_L=2πfL=2π×50×0.1=31.42 [Ω]\)
\(X_C=\displaystyle \frac{1}{2πfC}\)
其中,\(f\) 表示频率(50Hz),\(L\) 表示电感值,\(C\) 表示电容值。
但是,由于本示例没有给出电容值,所以\(X_C\)=0 。
\(Z = \sqrt{50^2+(31.42-0)^2} \ = 58.71 [Ω]\)
电流 \(I\) 可通过电压和阻抗之间的关系求出。
\(I=\displaystyle \frac{V}{Z}=\displaystyle \frac{100}{58.71}=1.7035 [A]\)
功率因数 \(PF\) 是有功功率与视在功率的比值。
\(PF=\displaystyle \frac{R}{Z}=\displaystyle \frac{50}{58.71}=0.853\)
视在功率 \(S\) 是电压和电流的乘积。
\(S=VI=100×1.704=170.4 [VA]\)
因此,线圈的阻抗约为58.71Ω,电流约为1.704A,功率因数约为0.853,视在功耗约为170.4VA。
为了进一步提高功率因数,可以在线圈中添加改善功率因数的电容器,因为这些电容器可发挥无功电流发生器的作用,从而可降低线圈消耗的无功功率,进而减少总耗电量。
了解功率因数的特性
了解功率因数的特性对于更大程度地提高电力系统的效率而言至关重要。功率因数表示电流和电压之间的相位差;其值越接近1,效率越高。功率因数低会导致无功功率增加,造成电能浪费和设备负荷增大。
功率因数与交流电:通过有功功率和视在功率理解功率因数
要很好地了解功率因数,必须理解它与交流电之间的关系。可以将功率因数视为“功率三角形”。在功率三角形中,三边分别表示有功功率、无功功率和视在功率。
上述示例在功率三角形中表示如下:
要很好地了解功率因数,理解它与交流电之间的关系至关重要。可以将功率因数视为“功率三角形”。在功率三角形中,三边分别表示有功功率、无功功率以及视在功率。
上述示例在功率三角形中表示如下:
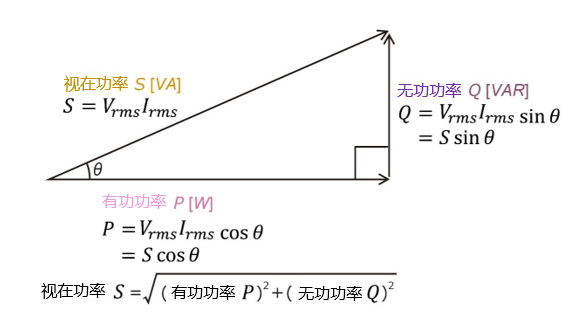
功率三角形是直角三角形,其斜边表示视在功率\(S\) ,底边表示有功功率\(P\),高度表示无功功率\(Q\)。每条边的长度定义如下:
・视在功率
\(S=V_{\text{rms}}\ I_{\text{rms}}\ [VA]\)
其中,\(V_{\text{rms}}\)是电压的有效值,\(I_{\text{rms}}\)是电流的有效值。
・有功功率
\(P=V_{\text{rms}}\ I_{\text{rms}}\ cos\theta = S\ cos\theta\ [W]\)
其中,\(\theta\)表示电压和电流之间的相位差。
・无功功率
\(Q=V_{\text{rms}}\ I_{\text{rms}}\ sin\theta\ = S\ sin\theta\ [VAR]\)
如果将这些关系直观地用一个“三角形”来看,可以得到以下三角关系:
\(S^2=P^2+Q^2\)
\(S=\sqrt{P^2+Q^2}\)
・功率因数
功率因数 cos\(\theta\)用有功功率\(P\) 与视在功率\(S\)之比来表示。
\(cos\theta = \displaystyle \frac{P}{S}\)
功率因数越接近1,意味着负载越接近理想的阻性负载,功率传输效率越高。相反,如果功率因数低,则意味着负载消耗了更多的无功功率,供电效率降低。
相位差对功率因数的影响
相位差对功率因数的影响是左右着电力系统效率的关键因素。功率因数(Power Factor)由电压和电流之间的相位差来决定的。下面来回顾一下功率因数的公式:
\(PF=cos\theta\)
可见,这里的相位差是衡量电力利用效率的指标。在交流电路中,波形的偏移角度以“相位差”来表示。电流波形和电压波形之间通常存在相位差。
相位差以“角度”来表示,一般电压超前时为正相位差,电流超前时为负相位差。
当存在相位差时,有功功率和无功功率的比例会发生变化。这会导致功率因数更低,电能质量更差。
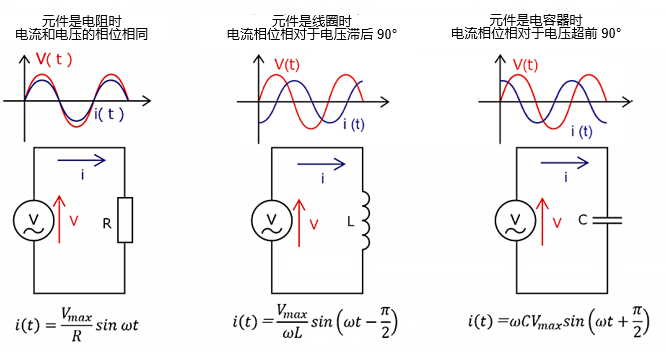
例如,在只有电阻的电路(纯电阻电路)中,电压和电流具有相同的相位。这种情况的相位差为0度,功率因数为1(100%)。也就是说,全部电力都被作为有功功率消耗,因此系统的工作效率非常高。
而在只有线圈的电路中,电流相对于电压滞后90度。此时的相位差为90度,功率因数为\(0\)。这意味着全部电力都被作为无功功率消耗,实际上处于电力完全没有作功的状态。同样,在只有电容器的电路中,电流相对于电压超前90度,因此功率因数还是\(0\)。
除了这些极端情况外,相位差为0到90度之间的任何角度时,功率因数都是cos\(\theta\)的值。例如,当相位差为30度时,功率因数约为0.866,值小于1,效率比只有电阻的电路低,无功功率增加了。
功率因数下降会引起不必要的电能消耗,导致电力系统的效率显著降低。对于电力公司和设施管理者来说,低功率因数意味着额外的成本。为了避免这种情况,提高功率因数非常重要。通常可以利用电容和电感来校正相位差,通过减少电压与电流之间的相位差,来提高功率因数。
综上所述,相位差对功率因数的影响非常大,直接关系到电力系统的效率和经济性。通过采取适当的措施,可以减少电能浪费并更有效地利用电力。
什么是位移功率因数?
位移功率因数(Displacement Power Factor)是根据基波电压和电流之间的相位差计算出来的功率因数。在不存在谐波的理想条件下,位移功率因数与功率因数的含义相同。位移功率因数的公式如下:
\(DPF=cos\theta\)
其中,\(\theta\) 是基波的相位差。位移功率因数是用来评估系统的电能质量的基本指标。
什么是功率因数1?
功率因数1(Unity Power Factor)表示电压和电流之间没有相位差的状态。在该状态下,所有的功率都作为有功功率被消耗,不存在无功功率。功率因数1的状态用以下公式表示:
\(PF=cos0°=1\)
当功率因数为1时,系统运行效率非常高,能量损失最小。这是理想的供电目标状态。
什么是滞后功率因数?
滞后功率因数(Lagging Power Factor)是指电流滞后于电压的状态。这主要是由感性负载(例如电机和变压器)引起的。滞后功率因数的状态通过下列公式表示:
\(PF=cos\theta (\theta>0)\)
其中,\(\theta\)是电流相对于电压滞后的角度。如果滞后功率因数低,就会导致无功功率比例变高,电力系统的效率降低。要想改善滞后功率因数,通常需要使用电容器来补偿无功功率。电容器具有使电流超前的特性,因此可以抵消感性负载导致的延迟。
什么是超前功率因数?
超前功率因数(Leading Power Factor)是指电流相对于电压超前的状态。这种状态主要是由容性负载(例如电容器)引起的。超前功率因数的状态通过下列公式表示:
\(PF=cos\theta (\theta<0)\)
当功率因数以小于1的值超前时(例如,功率因数为 0.9),意味着电流的相位超前于电压的相位。当功率因数超前时,系统会产生无功功率,但该无功功率是负值(也就是将电力回馈给系统)。
如果超前功率因数较高,就有望提高电力系统的效率,但过高的超前功率因数会导致无功功率增加,对系统的稳定性产生不利影响。
功率因数校正
功率因数校正是一种能够减少电力系统中电流和电压相位差的技术。这种技术可以提高电能利用效率并降低成本。通过减少无功功率、尽可能地增加有功功率,还可以提高设备的耐用性。例如,改善家用和商用空调以及照明设备的功率因数,有望减少电费。尤其是在工业领域,功率因数校正对于大型用电设施而言非常重要。另外,提高整个供电系统的功率因数,可以减少功率损耗,提高电能传输的效率。
提高功率因数的具体方法
为了提高电路的功率因数而引入的装置和电路被总称为“功率因数校正电路”。
在直流电路中,平均功率可以通过\(V×I\)简单地计算出来。然而,在交流电路中情况却有所不同。交流电路中往往有线圈、绕组和变压器等电感元件,电流和电压的相位是存在偏移的。因此,平均功率会小于电流与电压的乘积。这种现象是因为在有电阻和电抗元件(一种电感元件)的电路中,还需要考虑到相位角\(θ\)。
因此最好记住:在计算交流电路中的平均功率时,不仅需要考虑电流和电压,还需要考虑相位差。
下面介绍功率因数校正电路的主要类型及其作用。
电容电路(并联)
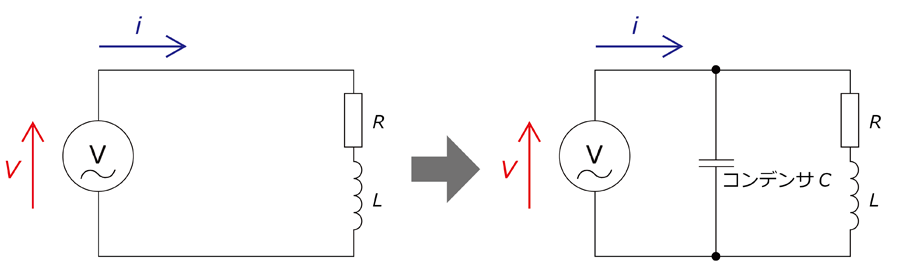
我们来看\(R 、L\)与电容器并联进行功率因数校正的情况。
1. 功率因数校正电路的理解与计算方法
(1) \(R – L\)串联负载的阻抗
首先,我们来探讨由电阻\(R\)和电感\(L\)串联连接的负载。其阻抗为:
\(Z_{RL}=R+jX_L=R+j(\omega L)\)
(2) 与电容器并联
将其与电容器\(C\)并联连接时,整个电路的导纳为:
\(Y_{total}=\displaystyle \frac{1}{Z_{RL}}+\displaystyle \frac{1}{Z_C}=\displaystyle \frac{1}{R+j\omega L}+j\omega C\)
因此,整个电路的阻抗\(Z\)为:
\(Z=\displaystyle \frac{1}{Y_{total}}\)
2. 功率因数校正电容器容值的推导
下面,我们在\(R- L\)串联负载上并联插入电容器\(C\),并推导出将目标功率因数\(PF_{target}\)校正至0.95所需的电容器容量\(C\),同时附上中间计算公式。
- 频率:f=50Hz
- 电感:\(L\)=0.1H
- 电阻:\(R\)=50Ω
- 目标功率因数:\(PF_{target}\)=0.95
- 电容器容量:\(C\) (需要求的值)
(1) \(R – L\)串联负载的阻抗与相位角
首先,角频率\(ω\)为:
\(\omega=2\pi f=2\pi\times50=100\pi\ (rad/s)\)
电感的电抗为:
\(X_L=\omega L=\left(100\pi\right)\times0.1=10\pi\approx31.416\mathrm{\Omega}\)
\(R – L\)串联电路的阻抗为:
\(Z_{RL}=R+jX_L=50+j31.416\left(\mathrm{\Omega}\right)\)
其大小为:
\(\left|Z_{RL}\right|=\sqrt{R^2+X_L^2}=\sqrt{{50}^2+{31.416}^2}\approx\sqrt{2500+986.2}\approx59.03\mathrm{\Omega}\)
相位角\(θ_1\)(电压相对于电流所滞后的角度)为:
\(\theta_1 = \tan^{-1}\left(\displaystyle \frac{X_L}{R}\right) = \tan^{-1}\left(\displaystyle \frac{31.416}{50}\right) \approx 32.1^\circ\)
所以,仅考虑\(R- L\)串联负载时的功率因数\(PF_1\)为:
\(PF_1 = \cos(\theta_1) \approx \cos(32.1^\circ) \approx 0.847\)
(2) 负载的有功功率\(P_L\)与无功功率\(Q_L\)
设线间电压(在这里假设为单相)为V、负载电流为IL,则
负载电流为:
\(I_L=\displaystyle \frac{V}{|Z_{RL}|}\)
有功功率(平均功率)为:
\(P_L=VI_Lcos{\mathrm{\theta}_1}=V\times\displaystyle \frac{V}{|Z_{RL}|}\times c o s{\mathrm{\theta}_1}=\displaystyle \frac{V^2}{|Z_{RL}|}\times c o s{\mathrm{\theta}_1}\)
无功功率为:
\(Q_L=VI_Lsin{\mathrm{\theta}_1}=\displaystyle \frac{V^2}{|Z_{RL}|}\times s i n{\mathrm{\theta}_1}\)
或者:
\(Q_L=P_Ltan{\mathrm{\theta}_1}\)
3. 目标功率因数补偿与电容器容量
(1) 所需的无功功率补偿量
电容器应补偿的无功功率\(Q_C\),是原负载所具备的\(Q_L\)与实现了目标功率因数时的无功功率之差。
原相位角:\(θ_1\)
目标功率因数 \(PF_{target}\)=0.95时的相位角:\(θ_2\)
\(\mathrm{\theta}_2={cos}^{-1}{(0.95)}\approx18.19°,tanθ2≈0.3287\)
所以,
\(Q_C=Q_L-Q_{new}=P_L(tan{\mathrm{\theta}_1}-tan{\mathrm{\theta}_2})\)
由于已经求出
\(\mathrm{\theta}_1\approx32.1°⇒ tanθ1≈XLR=0.6283\)
\(\mathrm{\theta}_2={cos}^{-1}{(0.95)}\approx18.19°⇒ tanθ2≈0.3287\)
所以,
\(tan{\mathrm{\theta}_1}-tan{\mathrm{\theta}_2}=0.6283-0.3287=0.2996\)
结果是:
\(Q_C=P_L\times0.2996\)
(2) 电容器的无功功率与容抗
并联连接的电容器会被施加与电路相同的电源电压\(V\),因此其无功功率为:
\(Q_c = \displaystyle \frac{V^2}{X_c}, \quad X_c = \displaystyle \frac{1}{\omega C}\)
另一方面,由于
\(V=I_L|Z_{RL}|\)
因此
\(Q_C=\displaystyle \frac{{(I_L\left|Z_{RL}\right|)}^2}{X_C}=\displaystyle \frac{I_L^2(R^2+X_L^2)}{X_C}\)
进一步推导得出:
\(X_C=\displaystyle \frac{R^2+X_L^2}{X_L-Rtan{\mathrm{\theta}_2}}\)
代入具体数值后得出:
・\(R^2+X_L^2={50}^2+{31.416}^2\approx3486.2\)
・\(X_L-Rtan{\mathrm{\theta}_2}=31.416-50\times0.3287\approx31.416-16.435\approx14.981\)
\(X_C\approx\displaystyle \frac{3486.2}{14.981}\approx232.7\mathrm{\Omega}\)
(3) 容量\(C\)的计算
根据电容电抗计算电容器的容量\(C\):
\(X_C=\displaystyle \frac{1}{\omega C}=\displaystyle \frac{1}{2\pi fC}\)
所以
\(C=\displaystyle \frac{1}{2\pi f X_C}=\displaystyle \frac{1}{2\pi\times50\times232.7}\approx\displaystyle \frac{1}{314.159\times232.7}\approx1.37\times{10}^{-5}F=13.7\mu F\)
因此,可以实现\(PF_{target}\)=0.95以上这一目标功率因数所需的功率因数校正电容器的电容量约为13.7μF。
有源滤波电路、功率因数补偿装置
有源滤波电路可用来补偿非线性负载产生的谐波。利用这种电路可以减少无功功率并提高功率因数。
功率因数补偿装置通过实时监控电流的流动并控制适当容量的电容器组,来优化功率因数。利用这种装置可以应对急剧的负载波动。
电容电路(串联)
接下来,我们来看一下将\(R、L、C\)全部串联连接时的情况。
1. 串联电路的阻抗
整个电路的阻抗\(Z\)为:
\(Z=R+j(X_L-X_C)\)
其大小(绝对值)为:
\(|Z|=\sqrt{R^2+{(X_L-X_C)}^2}\)
2. 串联电路的功率因数
因此,这个串联电路中的功率因数\(PF\)可以用以下公式来表示:
\(PF=\displaystyle \frac{R}{\sqrt{R^2+{(X_L-X_C)}^2}}\)
这是众所周知的RLC串联电路公式,在串联连接的情况下可以正确使用。
3. 与实际功率因数校正的差异
实际上在商用电力系统或电机负载等应用中进行功率因数校正时,虽然在理论上将\(R、L\)和\(C\)全部串联起来进行功率因数校正的方法是可行的,但在实际设备中这种方法并不常用。大多数情况下是采用“负载(\(R-L\))与电容器并联连接”的方式。这是因为用电容器的无功电流来抵消供给侧角度的“无功电流”是很方便的。
4. 串联\(R-L\) + 并联\(C\)的注意事项
在“\(R\)与\(L\)串联连接,并与\(C\)并联连接的电路”中,由于需要考虑并联合成,所以并不能简单地使用下面的公式:
\(PF=\displaystyle \frac{R}{\sqrt{R^2+{(X_L-\displaystyle \frac{1}{X_C})}^2}}\)
要注意避免误用。
功率因数的实际应用示例
改善功率因数与提高电能利用效率息息相关,能够带来更好的经济效益。通过节约能源和延长设备的使用寿命,可以降低应用成本。
工业设备中的功率因数应用示例
工业设备中功率因数的实际应用案例主要与使用电机的工业设备有关。在这类工业设备中,可能存在相位差。例如,在感应电机等负载会波动的设备中,会产生相位差,相位差会影响有功功率的计算。电机在工业设备中的应用非常广泛,提高其效率和功率因数直接关系到提高能源利用效率和降低成本。下面是工业设备中的功率因数应用示例。
电机驱动设备
在工业设备中,传送带、电泵、风扇和压缩机等机器都是由电机驱动的。这些电机通常使用诸如感应电机和同步电机等类型的电机。电机在启动时和负载波动时都需要大电流,这必然会给供电系统带来负荷。
如果功率因数低,电机将会产生较多的、额外的无功功率。这种无功功率会给供电系统带来负担,并降低电源效率。另外,供电系统中也会产生功率损耗。
提高工业设备中的功率因数,可以提高供电的稳定性和效率,从而节省电费。改善功率因数的工作有助于工业的可持续发展。
家用电器与功率因数
家用电器是我们日常生活中不可或缺的产品,这些设备的功耗与功率因数息息相关。功率因数会影响到这些电气设备的效率和供电系统的稳定性。下面来介绍功率因数在家用电器中的具体案例及其重要性。
家用电灯、空调、洗衣机和电脑等设备,都会消耗电力,都需要稳定的电力供应才能正常工作。但是,家用电气设备的功率因数可能比较低。功率因数低的设备会对供电系统产生额外的无功功率,从而使供电效率降低。最终会导致供电系统的整体效率下降,可能会增加消费者的用电成本(电费)。
具体而言,空调、洗衣机在启动时需要较高的启动电流,这会给供电系统带来较大的负荷。电脑和电子设备也是如此,而这会对供电稳定性产生不利影响,增加故障和数据丢失的风险。
因此,在家用电器的设计和选择过程中,功率因数都具有非常重要的意义。提高功率因数可以提高供电系统的整体效率,减少电力浪费,降低电费等成本。考虑家用电器的功率因数也有利于能源的可持续利用。
能源供应系统中的功率因数
功率因数在工业、家庭和能源供应等众多领域发挥着重要作用,对能源效率和能源经济性有重大影响。因此,大型电力系统需要适当的功率因数管理。下面将详细介绍功率因数在能源供应系统中的作用和影响。
作用和影响
- 提高供电效率:正确管理功率因数可提高电力的供应效率并更大程度地减少电力损耗,从而可以提高供电效率并有可能减少电费。
- 电压的稳定性:供电系统需要能够应对急剧的负载波动。改善功率因数可以提高供电稳定性并减轻电压波动,从而可以提高供电的可靠性并防止电子设备和设施发生故障。
- 减少功率损耗:功率因数低会引起供电系统不必要的功率损耗。改善功率因数可以减少不必要的功率损耗并防止电能浪费。从可持续能源供应的角度来看,这也非常重要。
对大型电力系统的影响
- 优化功率流:在大型电力系统中,改善功率因数可以优化功率流。可以调整电力供需,更大程度地减少电力损耗。
- 资源的有效利用:改善功率因数可以使供电系统能够更高效地利用资源。这对于提高发电效率和合理使用输电设备而言具有重大影响。
- 减少对环境的影响:改善功率因数意味着能源供应系统的运行效率更高,从而减少对环境的影响。有效利用能源有助于减少温室气体排放。
能源供应系统中的功率因数管理对于可持续的能源供应和提高电能质量来说是不可或缺的。改善功率因数可以实现高效的电力供应,减少对环境的影响并降低能源利用成本。