在交流电路中,电流和电压具有随时间的变化而变化的特性。要想准确理解这些变化对电路带来了哪些影响,就需要掌握复数知识,这一点非常重要。本文将带大家了解复数的具体计算方法,并直观地进行详细讲解。这将为更深入地了解交流电路的特性,实现更高效、更精密的电路设计奠定基础。
交流电路和复数基础知识
交流电路是指电流和电压随时间而变化的电路。了解与其相关的复数的基础知识,对于准确掌握交流电路的特性而言非常重要。下面将全面讲解复数的引入、计算、表示方法、基本概念。
复数的基本形式
复数通常由实部和虚部组成。复数的常见表示方式如下:
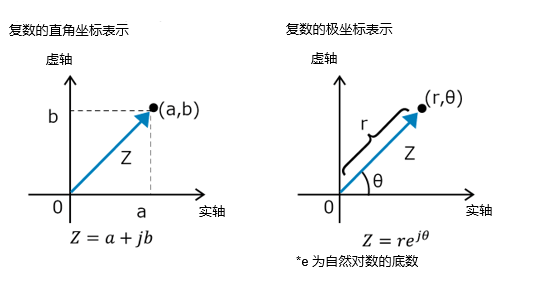
Z = a + jb
其中,a是实部,b是虚部,j是虚部单位。
将复数转换为极坐标形式也很 Z = rejϕ 常见,可以表示为。
复数的四则运算
加法和减法:复数的加法和减法分别计算实部和虚部。
例如,复数 Z1 = a1 + jb1 和 Z2 = a2 + jb2 之和为 Z1 + Z2 = (a1 + a2) + j(b1 + b2)。
乘法:复数的乘法是通过将实部之间和虚部之间分别相乘,利用虚数单位的平方为负的性质来计算的。
例如,复数 Z1 = a1 + jb1 和 Z2 = a2 + jb2 之积为: Z1 * Z2 = (a1 * a2 – b1 * b2) + j(a1 * b2 + a2 * b1)。
除法:复数除法是通过将分母和分子同时乘以分母的共轭复数来计算的。
例如,复数 Z1 = a1 + jb1 与 ![]() Z2 = a2 + jb2 的商为:
Z2 = a2 + jb2 的商为:
阻抗的复数表示
电路的阻抗是通过复数表示的。电阻、电感和电容均以复数表示,并且使用复数运算来计算它们的阻抗。
作为在交流电路分析中的应用,可以通过复数运算进行计算,优化电路的阻抗(阻抗匹配),从而尽可能提高能量传输效率。这可以提高电路之间的信号传输和电能传输的效率。
另外,奈奎斯特图是利用复数分析直观地了解系统稳定性和频率响应性能的工具之一。这种工具是在复平面上绘制传递函数,有助于把握系统的行为。
除此之外,博德曼定律也有助于提高电路性能,该工具提供了一种使用复数分析来优化电路带宽和信噪比的方法。
数学背景
数学背景是理解交流电路和复数的基础,对于电子电路的分析和设计而言是必不可少的。下面将介绍欧拉公式、三角函数、微分、积分和绝对值等对理解交流电路和复数至关重要的概念。
欧拉公式
欧拉公式在复数表示中发挥着核心作用。该公式结合了指数函数和三角函数,被用于以极坐标形式或直角坐标形式简洁地表示复数。
1. 复指数函数的定义
复指数函数用欧拉数e定义如下:
![]()
其中j是虚数单位。
2. 欧拉公式的推导
当将复数Z设为 Z = a + jb ,并用复指数函数来表示时,公式如下:
![]()
将前面的复指数函数定义代入该公式,可得到以下公式:
![]()
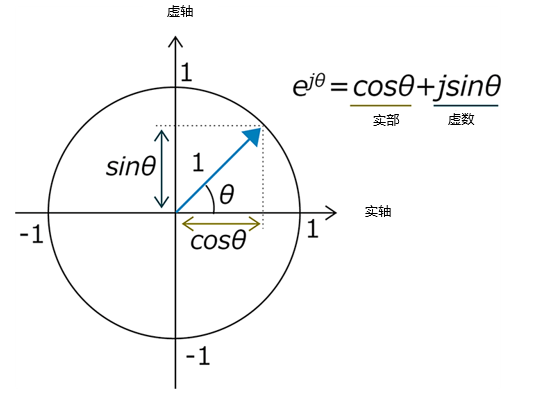
尤其是当 Z = jΘ 时,得到 a = 0 , b = Θ 。整理该公式后,可以推导出欧拉公式:
![]()
欧拉公式的应用示例
使用了欧拉公式的复数极坐标形式是一种用极坐标表示复数的方法。极坐标格式主要用三角函数和旋转的概念来表达,当复数z表示为“rejθ”时,由以下元素组成:
1. 复数的极坐标形式
复数z以极坐标形式表示如下:
![]()
其中,r表示复数的大小(绝对值),θ表示复数的相位角。这是使用欧拉公式推导出来的。
2. 利用欧拉公式推导
用欧拉公式 ![]() 推导极坐标形式:。
推导极坐标形式:。
![]()
在这种形式中,三角函数的性质显而易见,复数在复平面上被分解为角度和大小。
3. 极坐标形式的含义
大小 r:距复数原点的距离,表示绝对值。
相位角 Θ:复数相对于x轴逆时针形成的角度,仍然以弧度为单位。
4. 在图形上的表示
复数 ![]() 是指复平面上与原点相距 r 、相对于x轴旋转 Θ 的点。这就是根据三角函数的性质推导出来的圆周运动概念。
是指复平面上与原点相距 r 、相对于x轴旋转 Θ 的点。这就是根据三角函数的性质推导出来的圆周运动概念。
5. 欧拉公式的优异特性
通过欧拉公式将三角函数和指数函数关联起来,可以使复数的操作和分析更加轻松、容易。极坐标形式在复数的乘法和除法等计算可以简单地表示为角度的加减法方面尤其方便。
6. 复数的乘法和除法
使用极坐标形式,可以轻松计算复数的乘法和除法。
乘法:
![]()
除法:
![]()
三角函数
三角函数常被用于交流电路和正弦波的分析。特别是在正弦波的表述中,会频繁出现正弦和余弦。所以需要了解三角函数的基本性质和图形的特点,掌握交流电路中波形的特性。
正弦函数
y=sinθ
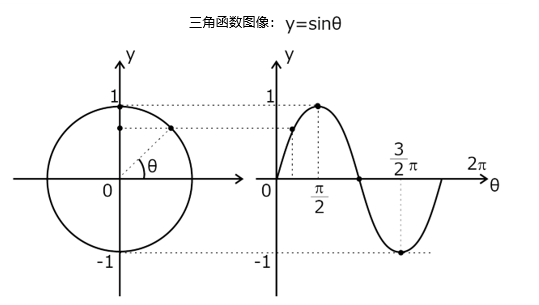
周期性:正弦函数是周期性的,周期为2π或360度。
振幅:振幅为1,在-1和1之间振荡。
对称性:是偶函数,sin(-θ)=-sin(θ)
最大最小值:最大值为1,最小值为-1。
相位差:sin(θ+π)=-sin(θ) 相位差π表示相位相反。
余弦函数
y=cosθ
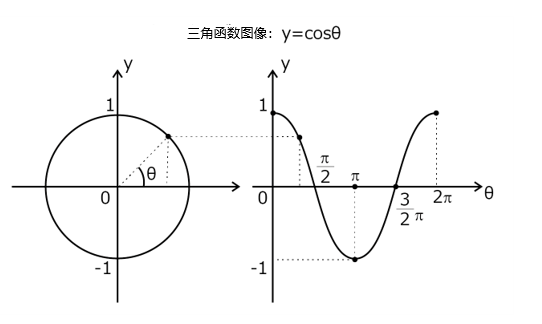
周期性:余弦函数也是周期性的,周期为2π或360度。
振幅:振幅为1,在-1和1之间振荡。
对称性:是偶函数,cos(-θ)=cos(θ)
最大最小值:最大值为1,最小值为-1。
相位差:cos(θ+π)=-cos(θ) 相位差π表示相位相反。
正切函数
![]()
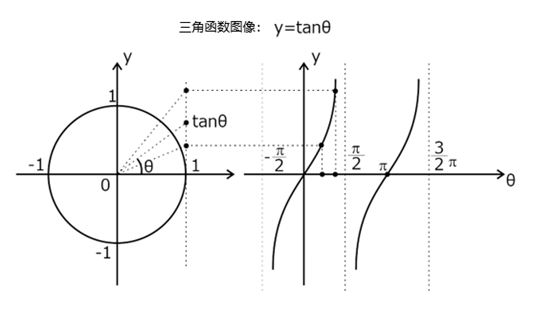
周期性:正切函数是周期性的,周期为π或180度。
发散点:在余弦函数变为0的点,正切函数发散。
微分和积分
微分和积分是把握电流和电压变化所需的数学手法。在交流电路的分析过程中,对于“随时间的变化”的考量是非常重要的。所以需要了解微分和积分的概念,以把握交流电路中信号的时间特性。
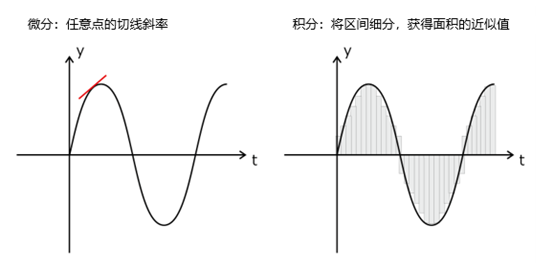
微分的概念
微分是描述函数变化率的一种方式,表示某个点的瞬时变化。对函数f(x) 关于 x 进行微分,可以获得导函数 f’(x)。导函数表示原函数的斜率,定义为:
![]()
积分的概念
积分是计算函数面积和累积的一种方式,通过将微小区间相加来获得。对函数 f(x) 关于 x 进行微分可以获得不定积分∫f(x)dx 或定积分![]() 。不定积分用来求原函数,定积分用来表示区间 [a,b] 中的面积。
。不定积分用来求原函数,定积分用来表示区间 [a,b] 中的面积。
∫f(x)dx = F(x) + C
其中,F(x) 是f(x) 的原函数,C 是积分常数。
交流电路中信号的时间特性
交流信号的表示
在交流电路中,通常使用随时间变化的信号。交流信号一般用正弦波来表示,公式如下:
V(t)=Vmax * sin(ωt+θ)
其中Vmax是振幅,ω 是角频率,t 是时间,θ 是初始相位。
信号的微分
信号的微分表示随时间的变化率。对交流信号 V(t) 进行微分即可得到导函数。
![]()
这是原信号的振幅乘以角频率得到的值,表示信号的瞬时变化率。
信号的积分
信号的积分表示信号的面积和累积。对交流信号 V(t) 进行积分可得到:
![]()
将原信号的振幅除以角频率,然后乘以负号,得到余弦波的积分。积分常数C是积分过程中的积分常数。
信号微分和积分的意义
微分:信号的微分表示变化率和瞬时行为,用于了解电路的响应性能和特性。
微分:信号的微分表示变化率和瞬时行为,用于了解电路的响应性能和特性。
绝对值
复数的绝对值表示其大小,即交流电路中的振幅或信号的强度。了解绝对值的计算方法及其应用,有助于正确理解复数的表现。这将能够通过数学方式来预测电路的行为。
1. 复数的形式
复数 z 通常采用“z=a+bj”的表示形式。其中,a 是实部,b 是虚部。根据该表示形式来确定求绝对值的方法。
2. 绝对值的计算公式
复数 z=a+bj 的绝对值(模)可通过下面的公式求出:
![]()
当在复平面上考虑复数时,表示从原点到该点的距离,适用勾股定理。
3. 复平面上复数的含义
当在复平面上绘制复数 z=a+bj 时,在直角坐标系中显示为点 (a,b)。该点与原点之间的距离为绝对值,可视其为振幅或信号的强度。
4. 振幅和信号强度的应用
a. 振幅的概念
在交流电路中,复数通常被转换为以振幅和相位角表示的极坐标形式。其中,r 表示振幅。该振幅与绝对值一致。
![]()
b. 信号强度的概念
振幅表示信号的强弱,振幅越大信号越强,振幅越小信号越弱。尤其是在交流电路中,电压和电流的振幅表示信号的强度和能量的传输量。
5. 简单示例
例如,复数z=3+4j的绝对值计算如下:
![]()
这表示从原点到点(3,4)的距离。振幅和信号强度也可以用同样的方式计算。
正弦波和交流电路
在交流电路中通常使用正弦波。交流电压的公式如下:
![]()
其中 Vmax 是振幅,ω 是角频率,t 是时间,θ 是初始相位。
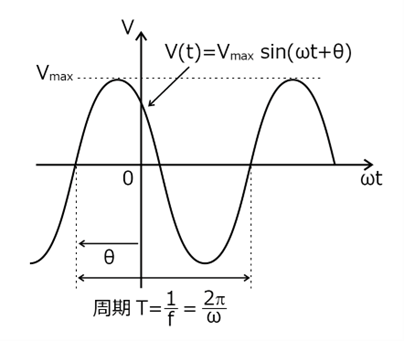
振幅:波形的最大高度。电压的振幅表示功率的传输量。
周期:完成一个周期所需的时间。
角频率:用 ω=2πf 表示,其中,f为频率。
初始相位:时间0时的相位角。
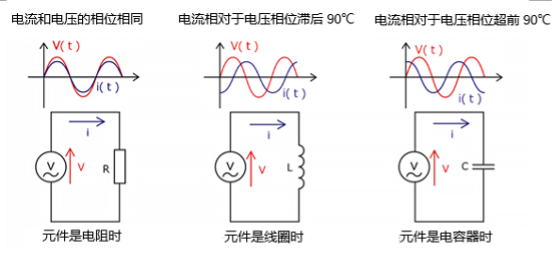
电压和电流的相位差与相移
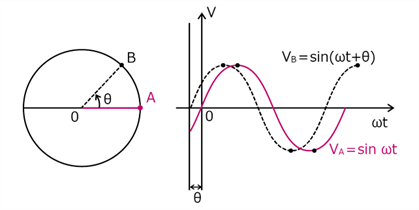
相位差和相移是表示交流电路中波形的时间关系的重要概念。下面将详细介绍这些概念。
相位
相位是表示电压和电流波形随时间偏移程度的指标。相位通常用弧度或度表示,在周期波形中是恒定角度。正弦波的相位从0度或0弧度的位置开始,并随着时间的推移而增加。
在交流电路中,电压和电流的相位用角度表示,常用下面的表达式来表示:
![]()
其中,V(t) 是时间 t 处的电压值,Vmax 是振幅(最大值),ω 是角频率(乘以2π得到的值),θ 是相位(相位角)。
相位差
不同波形之间相位的差称为“相位差”。相位差通常以每周期的角度来表示。例如,如果两个波形从同一位置开始,则相位差为0度或0弧度。如果相位差为90度,则表示一个波形超前另一个波形1/4周期。
相移
相移是指波形随时间位移的现象。交流电路中的电阻(R)、电感(L)和电容(C)等元素和信号处理过程中都可能产生相移。当发生相移时,波形的波峰(峰值)会随时间而变化,可以显示出电路中的信号随时间滞后或超前了多少。
相移有两种数学表达方式,一种是时域的,另一种是复数形式的。
a. 时域表达式
![]()
其中,V1(t) 和V2(t) 是两个波形,θ1 和 θ2 是它们各自的相位。相移用“θ2-θ1”表示。
b. 复数形式的表达式
以复数形式表示时,相移是复数的乘积。当有两个复数 Z1 和 Z2 ,它们的相位分别为 θ1 和 θ2 时,则其表达式为
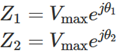
将这些复数相乘即可获得相移值。
![]()
其中 j 是虚数单位。
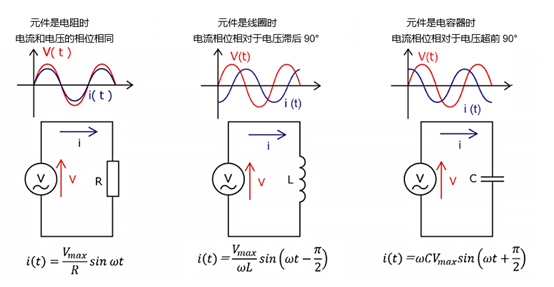
正相移
正相移表示波形在时间轴上滞后的状态。这通常可以认为是波形向右偏移。在仅连接了线圈(电感) L 的交流电路中,与施加给线圈(电感) L 的电压 VL 的相位相比,流过线圈(电感) L 的交流电流 IL 的相位超前![]()
负相移
负相移表示波形在时间轴上超前的状态。这通常可以认为是波形向左偏移。在仅连接了电容 C 的交流电路中,与施加给电容 C 的电压 VC 的相位相比,流过电容C的交流电流 IC 的相位滞后\![]()
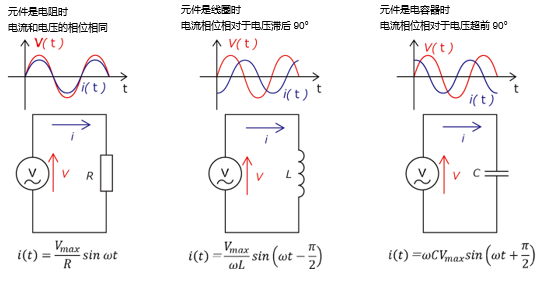
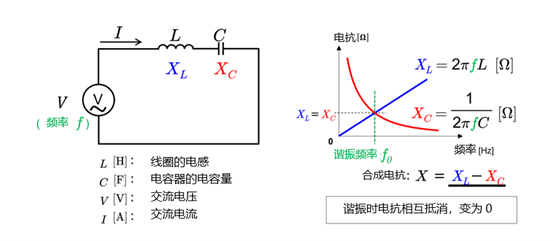
阻抗等电路元素与复数分析
组成交流电路的元素包括阻抗、线圈、电容和电阻等元素。特别是在电阻(R)、电感(L)和电容(C)组成的RLC电路中,复数分析(一种使用了复阻抗的电路分析方法)非常有助于了解特定频率下的表现。
串联电路的复数分析
串联电路是电阻 R 、电感 L 和电容 C 串联连接的电路。当使用复阻抗分析串联电路时,需要通过计算各元素的复阻抗来求出合成阻抗。
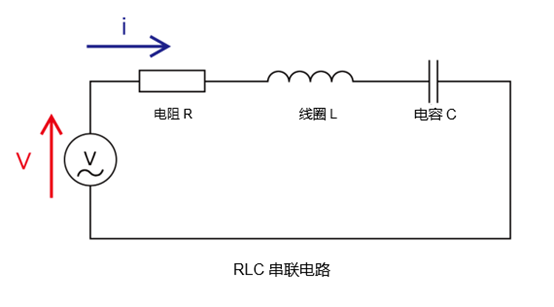
1. 电阻 R 的复阻抗
电阻的复阻抗 ZR 的实部为电阻值 R,虚部为零。
Z_R=R+j・0=R
2. 电感 L 的复阻抗
电感的复阻抗 ZL 中含有虚部成分,通过“ j ”表示。
ZL=jωL
其中, j 是虚数单位, ω 是角频率,L 是电感。
3. 电容 C 的复阻抗
电容的复阻抗 ZC 中含有虚部成分,通过“ j ”表示。
![]()
其中, j 是虚数单位,ω 是角频率,C 是电容。
4. 合成阻抗 Ztotal 的计算
在串联电路中,将各元素的复阻抗相加即可求出合成阻抗。
![]()
5. 稳态电流 I 的计算
利用合成阻抗可以求出稳态电流I,此时需要用到欧姆定律。
![]()
其中,V 是施加到电路的电压。
6. 稳态压降 VR ,VL,VC 的计算
利用欧姆定律可以计算出各元素的电压降。
VR=I・ZR
VL=I・ZL
VC=I・ZC
7. 各元素功率的计算
各元素的功率可通过电压降与电流的乘积计算出来。
PR=VR・I
PL=VL・I
PC=VC・I
并联电路的复数分析
并联电路是电阻 R 、电感 L 、电容 C 并联连接的电路。通过计算各元素的复阻抗并求出合成阻抗,可以分析电路的行为。
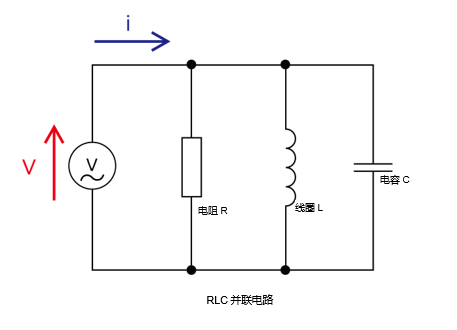
1. 电阻 R 的复阻抗
电阻的复阻抗 ZR 的实部为电阻值 R ,虚部为零。
ZR=R+j・0=R
2. 电感 L 的复阻抗
电感的复阻抗 ZL 中含有虚部成分,通过“ j ”表示。
ZL=jωL
其中,j 是虚数单位,ω 是角频率,L 是电感。
3. 电容 C 的复阻抗
电容的复阻抗 ZC 中也含有虚部成分,通过“ j ”表示。
![]()
其中,j 是虚数单位,ω 是角频率,C 是电容。
4. 合成阻抗 Ztotal 的计算
在并联电路中,将各元素的倒数相加即可求出合成阻抗:
![]()
5. 稳态电流 I 的计算
利用合成阻抗可以求出稳态电流 I ,此时需要用到欧姆定律。
I=V・Ztotal
其中,V 是施加到电路的电压。
6. 施加给各元素的电压 VR、VL、VC 的计算
利用欧姆定律可以计算出施加于各元素的电压。
VR=I・ZR
VL=I・ZL
VC=I・ZC
7. 各元素功率的计算
各元素的功率可通过电压降与电流的乘积计算出来。
PR=VR・I
PL=VL・I
PC=VC・I
实际应用
实际应用的重要性
1. 性能提升
复数分析的实际应用可以提高电子电路和系统的性能。高效的能量转换和信号处理,有助于提高系统的响应性能和可靠性。
2. 提高设计效率
复数分析所提供的数学方法,有助于进一步提高设计阶段的效率。基于准确计算的设计,可减少试错成本并缩短设计周期。
3. 提高可靠性
通过复数分析的实际应用,可以从理论上和数学角度准确了解电路和系统的工作,从而有助于提高系统的可靠性并提高故障排除效率。
4. 多学科应用
复数分析不仅适用于电气工程领域,还适用于控制工程、通信工程、声学工程等众多领域,因此,复数分析可为不同的领域解决问题。
实际应用示例
1. 阻抗匹配
阻抗匹配是在信号传输和电力传输中调整发送端和接收端的阻抗以实现能量传输最大化的方法。该方法可以尽可能地减少信号损失并提高系统效率。
2. 滤波器设计
在实际地电子电路中,会使用滤波器来控制信号的频率特性。利用复数分析,可以优化带通和衰减等特性并提取出所需的信号。
3. 功率分析
在实际的电源电路和电力传输系统中,功率、电流和电压的分析非常重要。利用复数分析方法来详细分析这些参数,可实现高效率的能量转换。
4. 信号处理
在音频处理和通信工程等信号处理领域,复数分析也特别常用。复数分析有助于提取特定频率分量以及调整信号的相位和振幅。
5. 控制系统
在控制系统中,可利用复数分析来评估系统的稳定性和响应速度。复数分析有助于了解控制对象和控制器的行为,以优化控制设计。
实例
最后,我们通过具体的例子来介绍至此所学知识的应用方法。通过问题和解答,来提高解决问题的能力、加深对复平面上的相位的理解、并培养实践技能。
通过使用复数分析方法,可对RC滤波器的特性进行数学建模。利用该方法设计截止频率是确保对象频率响应性能达到要求的关键步骤。可通过适当调整设计变量——截止频率和电容器容量来定制滤波器的性能。
背景
RC 低通滤波器是由电阻(R)和电容(C)组合而成的电路,用来使特定的频率分量通过。在这里将利用复数分析来设计在特定截止频率下 RC 滤波器的行为。
步骤1:确定规格
设截止频率为 fc。
设电容器的容量为 C。
步骤2:复数分析
- 1.计算阻抗
电容器的阻抗
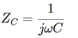
j 是虚数单位,ω=2πf是角频率。
- 2.计算合成阻抗
电阻的阻抗
ZR=R合成阻抗
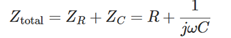
- 3.推导传递函数
传递函数
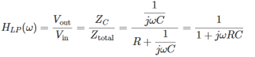
HLP(ω) 的频率依赖性推导。
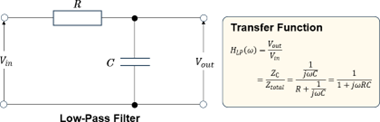
步骤3:设计截止频率
分析截止频率fC处的传递函数。
求出 HLP(ω) 为0.707(-3dB) 时的频率并将其作为 fC。
![]()
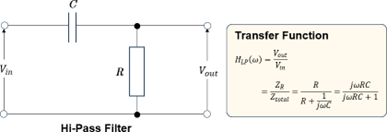
背景
RC高通滤波器是由电阻(R)和电容(C)组合而成的电路,用来使高频分量通过。在这里将利用复数分析来设计在特定截止频率下RC滤波器的行为。
![]()