目录
谐振电路是使用电感(L)和电容(C)在特定频率下引起谐振的电路。谐振电路分串联谐振电路和并联谐振电路两种。谐振时,串联谐振电路的阻抗最小,并联谐振电路的阻抗最大。这些特性被广泛应用于无线通信、滤波器设计和信号处理等各种电子设备。
本文将更详细地介绍谐振频率的计算方法和Q值(Quality Factor)的求法。准确计算谐振频率对于设计和优化谐振电路而言至关重要,而Q值是用来评价电路选择性和能量损耗的重要指标。理解这些概念有助于充分利用谐振电路的性能,设计出更高效、更精密的电子电路。
什么是谐振频率?
谐振频率是物体或系统自然振动的固有频率。当从外部以该频率提供能量时,会产生称为“谐振”的现象,从而使系统的振动被放大。要想深入了解这种现象,需要先了解“固有振动”的概念。固有振动是指物体受到外部冲击后以其自身的固有频率产生的自然振动。这个频率是由物体的形状、质量和弹性决定的,无论外部冲击的大小如何,物体只会以这个频率振动。例如,不同的打击乐器之所以会发出独特的音色,是因为它们会以自有的频率振动。
当以谐振频率发生谐振时,系统会非常有效地吸收和存储外部能量。例如,“荡秋千”就是一种能够以较小的力来增加秋千摆动幅度的简谐振动案例。这是通过利用秋千的固有频率从外部提供能量来放大振动幅度而实现的。
在电路中,通过电阻、电感(L)和电容(C)的组合来决定谐振频率,当电路在该谐振频率下工作时,电感和电容之间将会高效地传输“电磁能”,从而使整个电路存储的能量达到最大。这个原理已被广泛应用于无线通信、滤波和传感器技术等众多领域。正确理解并控制谐振频率,可以更大程度地提高相关系统的性能并实现高效率和高精度。
要理解谐振电路,首先需要了解“固有振动”和“谐振”现象。
“固有振动”是指当物体受到冲击时,该物体以其固有的频率振动的现象。
那么,什么是“以固有的频率振动”呢?例如,当敲击木琴(乐器)上的每个琴键时,或者当敲击有水的玻璃杯子边缘时,就会听到声音,无论是由谁来敲击,同样的东西发出的音调是相同的。
之所以音调相同,是因为木琴上每个琴键的材质和尺寸、玻璃的材质和厚度、水杯中的水位等条件决定了每次敲击时的振动频率(固有频率是固定的)。
如果持续对一个物体施加固有振动力,振动将与施加的振动力同步被放大。这种现象称为“谐振(共振)”。
例如,对摆动的秋千持续施力并继续晃动,秋千的摆动幅度会逐渐变大,这也是因为正在发生“共振”。
谐振电路中的谐振频率
谐振电路中的谐振频率是指电子电路发生谐振时的特定频率,在该频率下电路的阻抗达到最小或最大。谐振电路可以串联或并联设计,无论串联还是并联,谐振频率的计算公式是相同的。
谐振频率由下列公式表示:
\(\)
\(f_0 = \displaystyle \frac{1}{2\pi \sqrt{LC}} \, \text{[Hz]}\)
另外,谐振角频率(ω0)如下:
\(\omega_0 = \displaystyle \frac{1}{\sqrt{LC}}\)
要了解谐振电路,需要先了解谐振频率和谐振角频率,这很重要。谐振频率(f0)是电路能够最有效地传输能量的频率,在该频率下电压和电流会达到最大值。谐振角频率(ω0)以弧度每秒(rad/s)表示谐振频率,在计算和分析中经常会用到。
了解这些基本概念有助于更深入地了解谐振电路的工作原理及其特性。在谐振电路的设计和应用中,这些频率知识非常有用,因此在本文中会介绍相关的知识。
是否发生谐振与电抗息息相关。容抗XC和感抗XL分别定义如下:
\(X_C = \displaystyle \frac{1}{2\pi f C}\)
\(X_L = 2\pi f L\)
从公式可以看出,容抗和感抗都会随着频率的变化而变化。
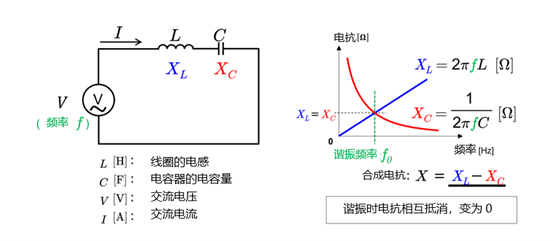
电感和电容的电抗相等是发生谐振的条件:
\(X_L = X_C\)
将其代入电感和电容公式中,可以得到:
\(2\pi f L = \displaystyle \frac{1}{2\pi f C}\)
求出该公式的频率(f)即可得到谐振频率(f0):
\(f_0^2 = \displaystyle \frac{1}{4\pi^2 LC}\)
\(f_0 = \displaystyle \frac{1}{2\pi \sqrt{LC}}\)
另外,谐振角频率(ω0)如下:
\(\omega_0 = \displaystyle \frac{1}{\sqrt{LC}}\)
谐振电路被广泛应用于通信、广播和模拟电子设备等众多领域,利用其特性,可以增强特定频率的信号。
什么是串联谐振电路?
串联谐振电路是串联连接电感器和电容器、使谐振频率下的阻抗最小的电路。该电路发挥滤波器的作用,会选择性地仅使某些特定频率通过。在无线电接收器和音频设备等强调特定信号的设备中应用广泛。
串联谐振电路的谐振频率由电感和电容的值决定,可进行精确的频率控制。通过设计串联谐振电路,可实现高性能电子设备的工作。
电阻(R)、电感(L)和电容(C)串联的电路中会发生谐振。谐振会发生在电容和电感的电抗相等的频率处。这种电路称为“RLC串联谐振电路”。
在RLC串联电路中,阻抗(Z)的表达式如下:
\(|Z| = \sqrt{R^2 + X^2} = \sqrt{R^2 + (X_L – X_C)^2}\)
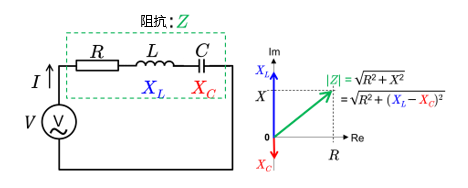
另外,发生谐振的条件是电感和电容的电抗相等时。
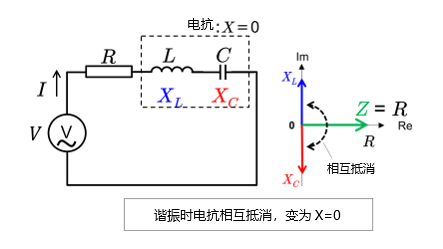
也就是说,在处于谐振状态的RLC串联电路中,阻抗(Z)的表达式如下:
\(|Z| = \sqrt{R^2 + 0^2} = R\)
从复阻抗来看,当电容和电感的电抗相等时,阻抗仅由电阻分量组成。
\(Z = R + j(X_L – X_C)\)
\(Z = R + j(\omega_0 L – \displaystyle \frac{1}{\omega_0 C}) = R + j\left(\displaystyle \frac{L}{\sqrt{LC}} – \displaystyle \frac{\sqrt{LC}}{C}\right) = R + j\left(\displaystyle \frac{\sqrt{L}}{\sqrt{C}} – \displaystyle \frac{\sqrt{L}}{\sqrt{C}}\right) = R\)
电感L和电容C的电抗在谐振频率处会相互抵消,因此看起来只有电阻(R)。
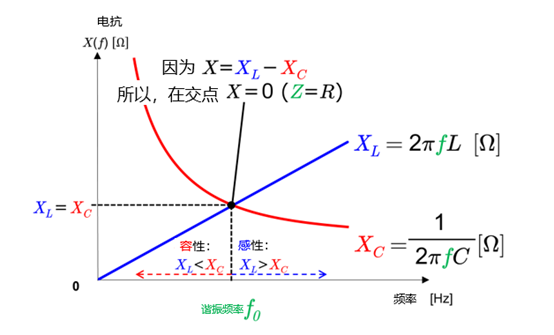
这可以使阻抗达到最小值,电路中的电流达到最大值。
\(I = \displaystyle \frac{V}{\sqrt{R^2 + (X_L – X_C)^2}} = \displaystyle \frac{V}{\sqrt{R^2 + 0}} = \displaystyle \frac{V}{R}\)
串联谐振电路在电气和电子电路中发挥着非常重要的作用。目前已被广泛应用于诸如AC电源滤波器、噪声滤波器、收音机和电视机的调谐电路等各种电气产品中,用以生成可接收特定频道的具有选择性的调谐电路,从而可以准确地选择和接收各种频率的信号。
什么是并联谐振电路?
并联谐振电路是电感和电容并联的电路,其特点是在特定频率下会发生谐振现象。这种电路适用于无线通信和滤波电路等强调和需要选择特定频率的众多电子设备。在谐振频率处,电感和电容的电抗会相互抵消,使整个电路的阻抗达到最大,特定信号被增强。
RLC并联谐振电路是电阻(R)、电感(L)和电容(C)并联连接的电路。这种电路的阻抗公式如下:
\(\displaystyle \frac{1}{Z} = \displaystyle \frac{1}{R} + \displaystyle \frac{1}{j \omega L} + j \omega C = \displaystyle \frac{1}{R} + \displaystyle \frac{-j}{\omega L} + j \omega C = \displaystyle \frac{1}{R} + j(\omega C – \displaystyle \frac{1}{\omega L})\)
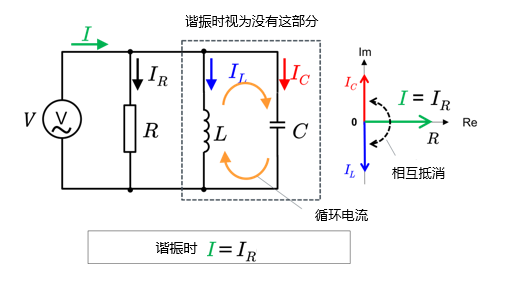
当RLC并联谐振电路正在发生谐振时,就像RLC串联谐振电路发生谐振时一样,电感L的电抗和电容C的电抗处于相互抵消状态。
\(\displaystyle \frac{1}{Z} = +j\left(\displaystyle \frac{\sqrt{C}}{\sqrt{L}} – \displaystyle \frac{\sqrt{C}}{\sqrt{L}}\right) = \displaystyle \frac{1}{R}\)
可见,在RLC并联电路中,当处于谐振状态时,阻抗(Z)也只有电阻分量。
\(Z = R \)
在RLC并联电路中,当处于谐振状态时,与RLC串联电路不同的是,此时阻抗最大(无穷大),电流最小(没有无电流流过,与电路断开时的状态相同)。
在RLC串联谐振电路和RLC并联谐振电路中,阻抗与电流之间的关系是不同的。流经RLC串联谐振电路的电流是电压除以阻抗的乘积,因此在发生谐振时阻抗为最小值(=R),电路电流为最大值。
而在RLC并联谐振电路中,发生谐振时导纳的虚部变为零,阻抗最大(=∞)。当阻抗最大时,电路电流受到限制,因此相当于电路断开状态。
RLC串联谐振电路和RLC并联谐振电路有很多共同之处,比如谐振频率的计算方法和发生谐振时Z=R等。但还有些不同之处需要掌握:在RLC串联谐振电路中,谐振时阻抗最小,电流最大;而在RLC并联谐振电路中,谐振时阻抗最大(无穷大),电流最小(没有电流流动,与电路断开时状态相同)。
谐振电路的Q值
“Q值(Quality Factor)”是量化谐振频率处信号曲线“尖锐程度”和选择性的重要指标,Q值越高,信号特性越尖锐,Q值越低,信号特性越平缓。该值可反映出电路有效存储能量和减少损耗的能力,对电子滤波器、振荡器和天线设计的精度影响非常大。
高Q值电路能够更精确地捕获窄带信号,是先进的通信技术和精密的传感器设计不可或缺的存在。选择和调整适当的Q值,是高性能电子设备设计中的关键要素。
另外,带宽与Q值成反比,表示谐振电路可有效通过的频率范围。
\(Q = \displaystyle \frac{\text{谐振频率下的信号强度}}{\text{带宽 BW}}\)
\(Q = \displaystyle \frac{\omega_0}{\omega_2 – \omega_1} = \displaystyle \frac{f_0}{f_2 – f_1}\)
下面,我们通过聚焦电路处于谐振状态时电流的表现以及电感(L)和电容(C)之间的相互作用,来了解RLC串联谐振电路中的Q值求法。发生谐振时,电流I恒定,电感和电容之间相互交换能量,因此这些因素产生的电抗相互抵消。
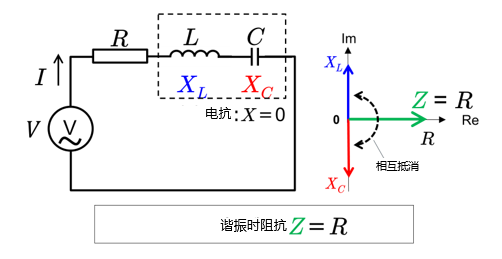
在这种状态下,Q值被定义为电阻器(R)的阻值与电感器的电抗之比,是表示电路选择性和谐振曲线锐度的指标。
\(Q = \displaystyle \frac{\omega_0}{\Delta \omega} = \displaystyle \frac{\omega_0}{\omega_2 – \omega_1} = \displaystyle \frac{1}{R} \sqrt{\displaystyle \frac{L}{C}} = \displaystyle \frac{\omega_0 L}{R}\)
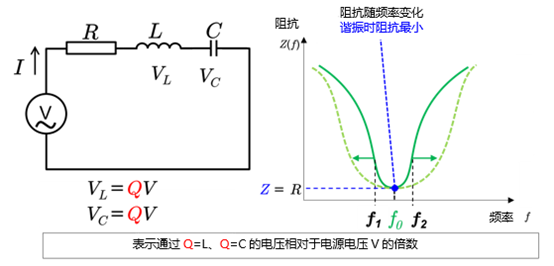
例如,下图表示RLC串联谐振电路中流动的电流大小“I”的频率特性。在电感(L)和电容(C)谐振的频率(角频率)处阻抗最小。
另外,Q值还发挥着谐振电路内电压放大倍数的系数的作用,表示通过电感器的电压被电阻分量放大了多少倍,即相对于电源电压的电压倍数。
另外,从图中还可以看出,当横轴为角频率时,电流的大小达到最大值。
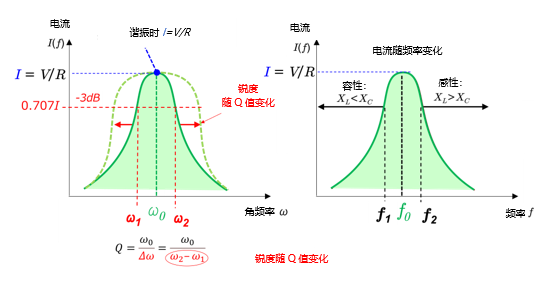
在RLC串联谐振电路中,通频带会随Q值变化,而在RLC并联谐振电路中,通频带是固定的。
RLC并联谐振电路中的Q值求法与谐振现象以及当时的电流和电压之间的关系密切相关。当发生谐振时,电路整体的电压V保持恒定,能量在电感器(L)和电容器(C)之间循环,这些元素的电抗相互抵消。在这种状态下,通过电感器和电容器的循环电流相等且相位相反,因此这些元件在导线间的功耗为零。
影响Q值的重要因素是流经电感器的循环电流与流经电阻器(R)的有效电流之比。该比值量化了电路的选择性和减少能量损耗的能力。Q值越高,意味着电路对窄通频带信号的选择性越好、能量损耗更少。谐振时电压恒定这一特性,表明并联谐振电路具有高效存储能量、高精度处理谐振频率附近信号的能力。
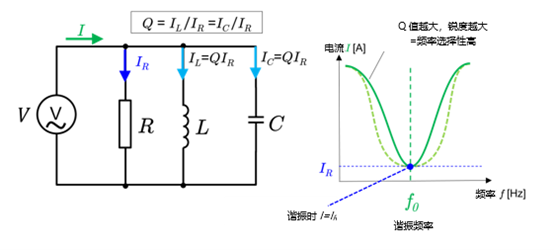
\(Q = \displaystyle \frac{I_C}{I_R} = \displaystyle \frac{I_L}{I_R}\)
\(Q = \displaystyle \frac{V}{\omega L} \div \displaystyle \frac{V}{R} = \displaystyle \frac{R}{\omega L} = \displaystyle \frac{R}{2\pi f L}\)
\(Q = \omega C ÷ \displaystyle \frac{V}{R} = \omega CR = 2\pi f CR\)
RLC并联电路的特性之一是谐振时的阻抗非常大,最终会限制流过电路的电流。这是因为电感器和电容器在谐振状态下交换能量,各自产生相位相反的电流,因此从外部看表现为高阻抗。这种现象可起到滤波器的作用,即电路仅在谐振频率下允许信号有效通过,在其他频率下则阻止信号通过。
另外,与RLC串联电路相比,LC并联电路中的电阻对电路通频带会起到阻尼作用。这种阻尼作用会控制谐振曲线的尖锐程度,通过抑制过于尖锐的谐振可实现更稳定的电路工作。
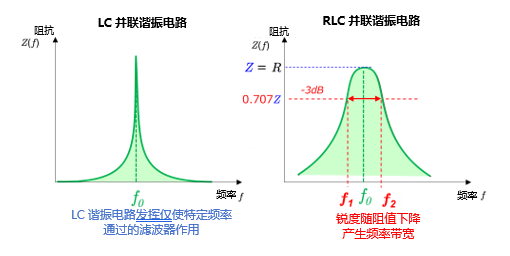
这里很重要的一点是并联谐振电路的Q值与串联谐振电路的Q值关系。具体而言,从计算公式看,并联谐振电路的Q值与串联谐振电路的Q值互为倒数。这是因为在串联电路中,Q值通过电感值与电阻值之比来表示;而在并联电路中,Q值通过该比值的倒数来表示。这种差异源于这两种电路在处理能量的方法上存在根本性差异。
谐振电路的使用示例
前面我们了解了串联和并联谐振电路,那么它们在我们的周围有哪些具体应用呢?
例如,串联谐振电路的应用包括电视机和收音机的无线电接收电路。
在这种应用中,利用串联谐振“在特定频率下电流最大”的特性,预先创建“谐振频率”等于想要接收的频率的电路,并实现在目标频率下流过大电流、在其他频率下几乎不流过电流的目的。
串联谐振电路还被用于AC电源滤波器、噪声滤波器等应用。
并联谐振电路的应用包括多频天线所用的陷波电路和宽带放大电路等。
▼关于利用电容器和线圈降低噪声的对策和EMC对策,可点击下面的链接搜索:
https://techclass.rohm.com.cn/knowledge/category/emc
可抑制谐振的阻尼电阻和铁氧体磁珠
随着电子元器件的体积越来越小、集成度越来越高,在使用RLC谐振电路时,噪声对策也变得越来越重要。这就需要充分了解利用电感器降噪的相关对策和频率控制方法。
如果电子电路中含有非预期的谐振电路,在达到谐振频率时就会产生非常大的电流和电压。因此,更容易引发噪声问题。也就是说,尽可能地消除电路中的意外谐振至关重要。可以使用阻尼电阻来抑制意外谐振。
还可以使用铁氧体磁珠来旁路噪声并将噪声转化为热能。
▼下面链接中的文章详细介绍了铁氧体磁珠、电感器的基本特性与噪声对策的关系以及作为低通滤波器的工作等内容:
https://techclass.rohm.com.cn/knowledge/emc/s-emc/04-s-emc/8138
深度理解谐振电路并在电子电路设计中灵活运用
谐振电路是一种利用了特定频率下的谐振现象的重要电子电路。目前,谐振电路已在众多电气产品设计中被用来提高产品品质。
随着电子元器件的体积越来越小、集成度越来越高,噪声对策也变得越来越重要。因此,了解使用电感器来降噪的方法是非常重要的。而加深对RLC谐振电路的理解,可以增加电感器自谐振和噪声对策相关知识,这些是非常重要的知识点。
另外,在产品设计中使用谐振电路,也是解决噪声问题的核心方法。希望大家以本文的内容和相关信息为参考,通过正确使用谐振电路来提高电路的品质。