\(\)

 

基尔霍夫定律是电路分析中最基础且不可或缺的定律，包括被称为“基尔霍夫电流定律（KCL）”的第一定律和被称为“基尔霍夫电压定律（KVL）”的第二定律。基尔霍夫电流定律的内容是，在电路中的任意一个节点，流入该节点的电流之和恒等于流出该节点的电流之和。而基尔霍夫电压定律的内容是沿闭合电路绕行一周的电压之和为零。通过应用这些定律，可以了解并有效分析复杂电路中的电流和电压分布。

在本文中，将从基尔霍夫定律的理论背景到其在实际电路问题中的应用、以及与欧姆定律的关系，全面介绍基尔霍夫定律。掌握基尔霍夫定律，是学习电路知识过程中不可或缺的一环，希望大家充分掌握其强大的分析能力。

基尔霍夫定律和电路基础知识

基尔霍夫第一定律和第二定律简介

基尔霍夫定律是电路分析中不可或缺的基本原理。该定律由两个重要部分组成，即基尔霍夫电流定律（KCL：Kirchhoff’s Current Law）和基尔霍夫电压定律（KVL：Kirchhoff’s Voltage Law）。

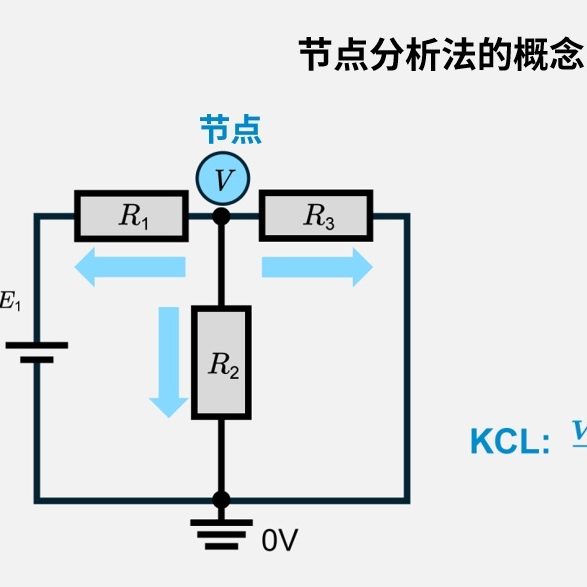
基尔霍夫电流定律（KCL）

基尔霍夫电流定律（第一定律）的内容是流入某一节点的电流之和等于从该节点流出的电流之和。用数学公式表示如下：

\(\small{\sum I_{in}=\sum I_{out}}\)

该定律表明，电荷不能在电路的节点处堆积。

基尔霍夫电压定律（KVL）

基尔霍夫电压定律（第二定律）的内容是沿闭合电路绕行一周的电压之和为零。该定律遵循能量守恒定律，用公式表述如下：

\(\small{\sum{V=0}}\)

该定律意味着电压降与电动势的总和是保持平衡的。

闭合电路与开路电路的区别

闭合电路和开路电路的概念在电路分析中非常重要。尤其是在应用基尔霍夫定律时，判别电路是否闭合非常重要。

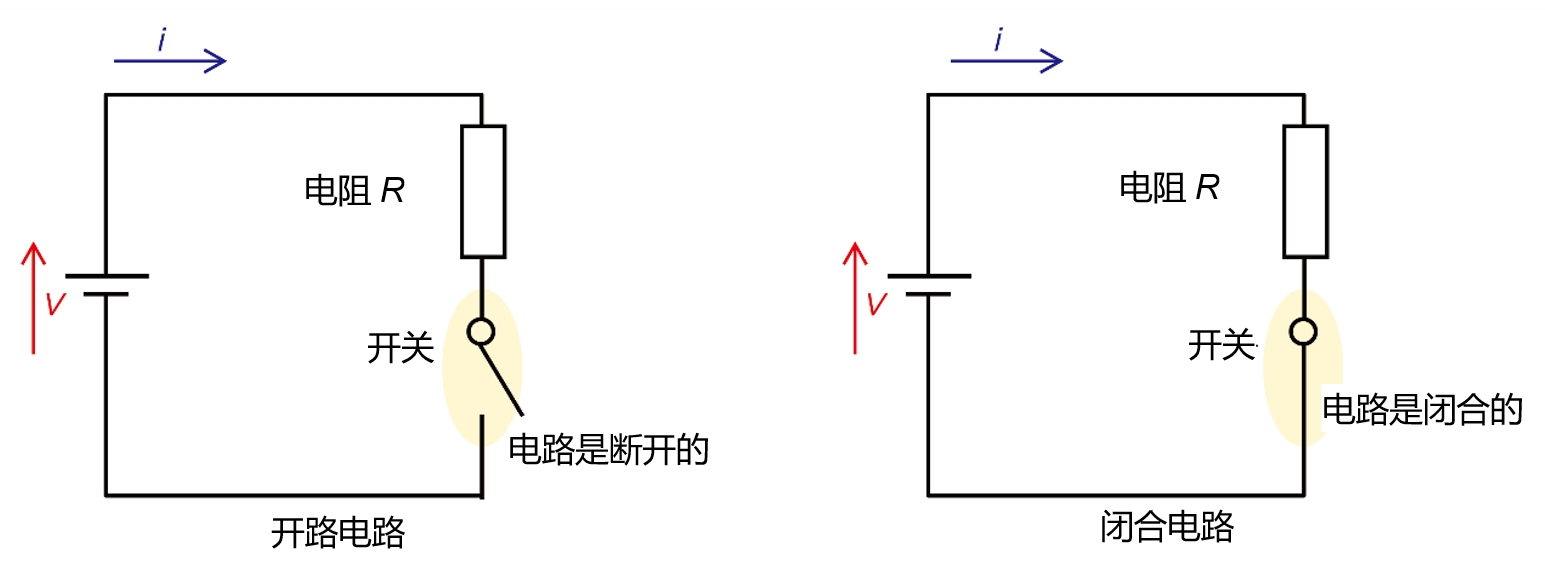
闭合电路

闭合电路是电流具有通过一系列的导体后返回电源的完整路径的电路，即电流从电源开始，流经一系列的电气元器件（电阻器、电容器、电感器等）后返回电源的路径。基尔霍夫定律适用于这种闭合电路。在闭合电路中，电流连续流动，电压降分散在电路中的各个元素上。

闭合电路的概念是电路设计和分析的核心。要想正确了解并预测电源、电阻器和其他电气元器件的动作行为，就需要掌握这些元素形成的闭合电路内的电流和电压之间的关系。另外，闭合电路在评估电路性能和诊断问题方面也发挥着重要作用。

开路电路

开路电路是指由于导体中间断开而没有完整的电流流动路径的电路。这种断开是由开关关闭、电路因物理因素断开或因某种原因造成的断裂而形成的。

尽管基尔霍夫定律不能直接应用于开路电路，但在分析包含开路电路的系统时发挥着重要作用。当电路无法正常工作或在设计阶段故意利用开路时，基尔霍夫定律是不可或缺的。在故障分析和故障排除中，开路很可能是造成问题的原因，在诊断中的作用很重要。另外，开路概念也适用于开关控制电路和电路暂时中断的设计。

基尔霍夫定律在电压和电流测量中的作用

电压测量基础知识和基尔霍夫定律的应用

电压测量是电路的关键要素，基尔霍夫定律在此过程中发挥着核心作用。

电压测量基础知识

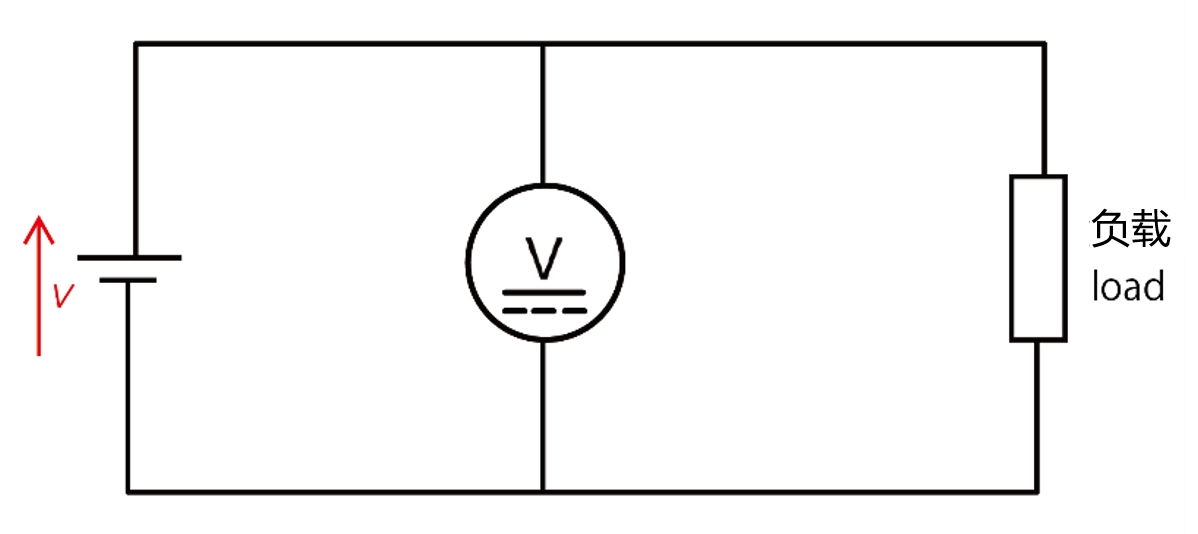
电压测量是测量电路中两点之间的电位差。这种测量通常使用电压表（伏特计）进行。测量时，应将电压表并联在要测量的两点之间。

基尔霍夫电压定律（KVL）的应用

基尔霍夫电压定律（KVL）的内容是沿闭合电路绕行一周的电压之和为零。利用该定律，可测量和计算电路中任何环路的电压。

\(\small{\sum{V=0}}\)

在电压测量中，利用KVL，可根据测量点之间的已知电压降来计算未知电压。

电流的测量方法和电路分析的重要性

电流测量和电路分析对于评估电路性能和安全性来说非常重要。

电流测量方法

电流测量是测量流经电路特定部分的电流强度的过程。这种测量通常使用安培表进行，需要将安培表串联到要测量的点。

基尔霍夫电流定律（KCL）与电路分析

基尔霍夫电流定律（KCL）的内容是流入某节点的电流之和等于流出该节点的电流之和。

\(\small{\sum I_{in}=\sum I_{out}}\)

利用该定律，能够分析电路中任意点的电流分布，并解释电流测量的结果。利用KCL，可以了解电流分布并评估电路功能。

联立方程式在电路分析中的应用

使用基尔霍夫定律设置联立方程式

使用基尔霍夫定律进行电路分析时，联立方程式的设置非常重要。

联立方程式的设置过程

1. 电路识别：识别电路中的所有节点（连接点）和回路（闭合电路）。
2. 基尔霍夫电流定律（KCL）的应用：在各节点建立“流入节点的电流之和等于从该节点流出的电流之和”的方程式。
   \(\small{\sum I_{in}=\sum I_{out}}\)
3. 基尔霍夫电压定律（KVL）的应用：在各环路建立“环路中的电压总和为零”的方程式。
   \(\small{\sum{V=0}}\)
4. 方程式求解：对所得方程式求解，求出未知的电流和电压。

实际的电路问题解决示例

下面我们通过基尔霍夫定律在解决实际电路问题过程中的应用示例，来了解该理论的具体应用。

例如，假设在一个简单的串联电路中连接了不同阻值的电阻器。要获取该电路中施加于每个电阻器的电压，需要按照下列步骤操作：

1. 应用KVL：设置整个电路适用的KVL方程式。
   \(V_{source}=V_1+V_2+\ldots+V_n\)
   其中，\(V_{source}\)表示电源电压，\(V_1,V_2,…,V_n\)表示施加于各电阻器的电压。
2. 应用欧姆定律：将欧姆定律应用于各电阻器，求出电压值。
   \(V_i=I\times R_i\)
   其中，\(I\)表示电路中的电流，\(Ri\)表示各电阻器的阻值。
3. 解方程：对这些方程式求解，即可求出施加于各电阻器的电压。

与电学理论的关系：欧姆定律和基尔霍夫定律

欧姆定律与基尔霍夫定律的结合

欧姆定律和基尔霍夫定律在电路分析中是相辅相成、相互补充的。

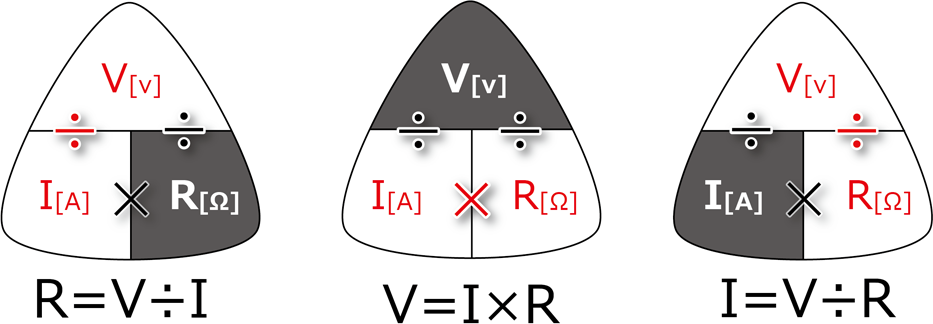
欧姆定律

欧姆定律阐明了导体中电压（\(\small{V}\)）与电流（\(\small{I}\)）之间的关系。该定律用下面的公式表示：

\(\small{V＝I×R}\)
其中，\(R\)示电阻值。

与基尔霍夫定律的结合

将基尔霍夫定律和欧姆定律结合起来，可以分析电路中电压和电流之间更复杂的关系。尤其是基尔霍夫电压定律（KVL）和电流定律（KCL）与欧姆定律相结合，有助于求出电路中的未知电压和电流。

这些理论在直流电路和交流电路中的应用

这些理论在直流（DC）电路和交流（AC）电路中的应用方法有所不同。

在直流（DC）电路中的应用

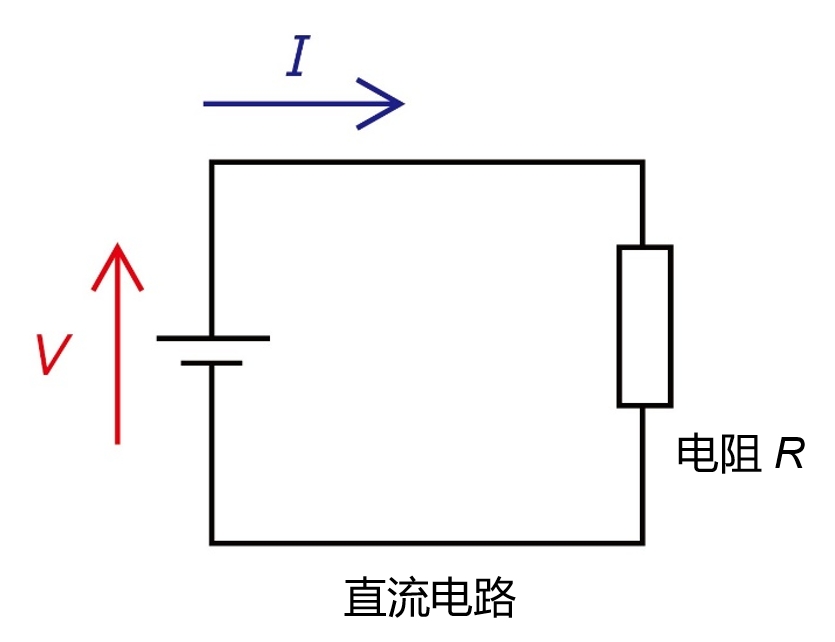
在直流电路中，电流沿恒定方向流动，电压也恒定。欧姆定律和基尔霍夫定律直接适用于直流电路的分析，用来计算电路中施加于各元器件的电压和流过的电流。

在交流（AC）电路中的应用

在交流电路中，电压和电流会随时间而变化。因此，在应用欧姆定律和基尔霍夫定律时，需要考虑交流电的特性。特别是相位差和交流电的频率发挥着重要的作用。

基尔霍夫定律的应用示例和计算方法

具体的计算示例和分步解说

下面分步骤来解说使用基尔霍夫定律的具体计算示例。

计算示例

例如，假设在一个有3个电阻器的简单电路中，电阻器R1、R2、R3串联连接，电源Vs连接到该电路。目的是求出施加于各电阻器的电压。

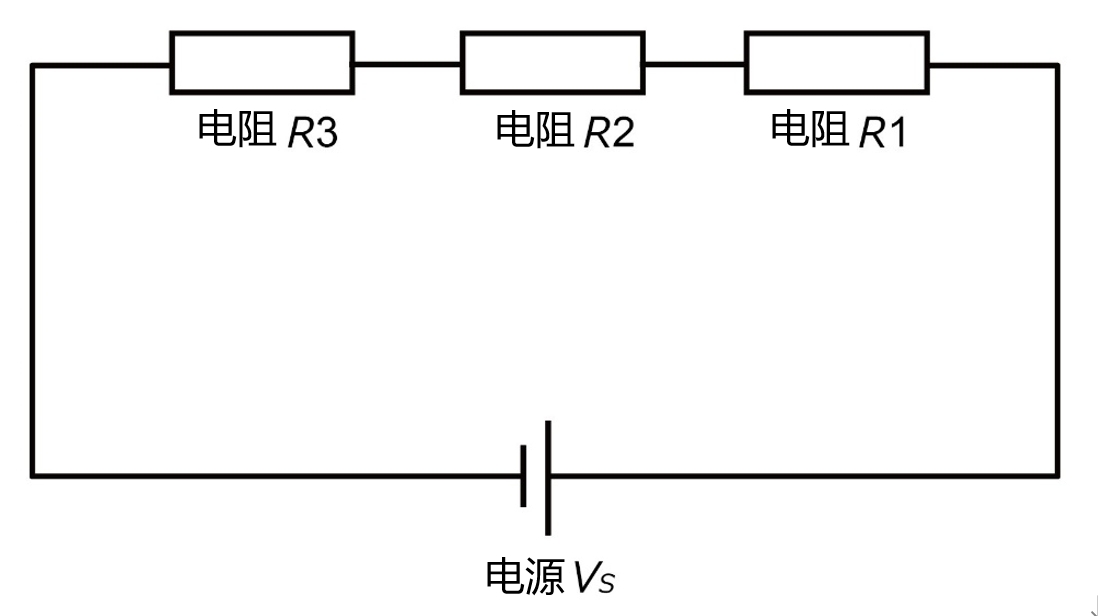
1.分析电路：首先，观察电路，识别各个元器件。

• 电源（电压：\(Vs\)）
• 电阻器1（阻值：\(R1\)）
• 电阻器2（阻值：\(R2\)）
• 电阻器3（阻值：\(R3\)）

2.应用基尔霍夫电压定律（KVL）:闭合电路中的电压之和为零。

\(\small{V_S＝V_1＋V_2＋V_3}\)

其中，\(\small{Vs}\) 表示电源电压，\(\small{V_1}\),\(\small{V_2}\),\(\small{V_3}\) 分别表示施加于电阻器 \(\small{R_1}\)、\(\small{R_2}\)、\(\small{R_3}\) 的电压。

3.应用欧姆定律: 将欧姆定律应用于各电阻器。

\(\small{V_i=I\times R_i}\)

4.计算: 使用电源电压和各电阻值来计算施加于每个电阻器的电压。

根据欧姆定律，各电阻器的电压可以计算如下：

・ \(\small{V_1＝I×R_1}\)
・ \(\small{V_2＝I×R_2}\)
・ \(\small{V_3＝I×R_3}\)

其中， \(\small{I}\) 表示流过电路的电流。

5.整理方程式

将前面得到的数值代入基尔霍夫电压定律的方程中，得到：

\(\small{V_S＝I×R_1＋I×R_2＋I×R_3}\)

从该方程式可以看出，串联电路中的电压降等于电源电压。

在难解问题中应用基尔霍夫定律

下面介绍如何在更复杂的电路中应用基尔霍夫定律。

难解问题示例

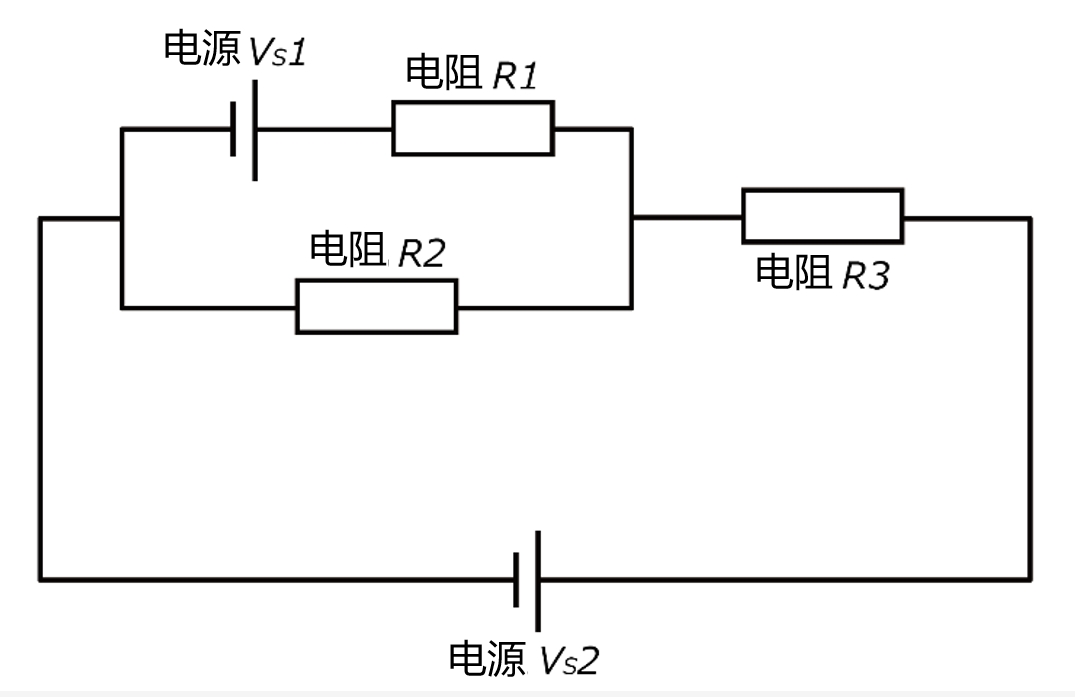
假设是一个包含多个电源和电阻器的电路。

• 电源1（电压：\(Vs1\)）
• 电源2（电压：\(Vs2\)）
• 电阻器1（阻值：\(R1\)）
• 电阻器2（阻值：\(R2\)）
• 电阻器3（阻值：\(R3\)）

电路连接情况如下：

• \(Vs1\) 和 \(R1\) 串联。
• \(R2\) 与该组合并联。
• 整个并联电路与 \(R3\) 串联。
• 最后，\(Vs2\) 连接在 \(R3\) 之后。

电路公式

以下公式成立：

• 闭合电路1（包括\(Vs1\), \(R1\), \(R2\)）：\(Vs1−I1⋅R1−I2⋅R2=0\)
• 闭合电路2（包括\(Vs1\), \(Vs2\), \(R3\)）：\(Vs1−I3⋅R3−Vs2=0\)
• 闭合电路3（包括\(Vs2\), \(R2\), \(R3\)）：\(Vs2−I2⋅R2−I3⋅R3=0\)

其中，\(\small{I1}\), \(\small{I2}\), \(\small{I3}\)表示流过各个电路部分的电流。

对于这样的电路，需要按照以下步骤进行分析：

1. 识别电路元素：识别电路中的所有电源、电阻器、节点和闭合电路。
2. 应用基尔霍夫定律：对每个闭合电路应用KVL，对每个节点应用KCL。
3. 设置联立方程式：设置用来将得到的方程一起求解的联立方程式。
4. 计算：对方程式求解，求出未知的电流和电压。

电位差和电动势：基尔霍夫定律的扩展

什么是电位差？与基尔霍夫定律的关系

电位差是电学中的基本概念，与基尔霍夫定律密切相关。

电位差的定义

电位差是两点之间电势（电能状态）之差，表示电荷从一点移动到另一点所做的功，以伏特（\(\small{V}\)）为单位进行测量。电位差\(\small{V}\) 用公式表达如下。单位为伏特（\(\small{V}\)）表示，可以用下面的公式表示：

\(\small{V＝W/Q}\)

其中，\(\small{V}\)表示电位差，\(\small{W}\)表示功，\(\small{Q}\)表示电荷。

电位差和基尔霍夫定律的关系

电位差的概念对于运用基尔霍夫定律来了解电路中的电压分布至关重要。例如，在包含多个电源和电阻器的电路中，可利用基尔霍夫定律来确定各部分的电位差。利用该定律，可以准确掌握电的源电位差在电路内的分配情况。

对电动势和基尔霍夫定律的综合理解

电动势是电源产生的电位差，与基尔霍夫定律结合起来理解很重要。

电动势的定义

电动势（EMF：Electromotive Force）是电源（比如电池和发电机）向电路提供的能量所产生的电位差。电动势代表电源向电路提供能量的能力，以伏特（\(\small{V}\)）为单位进行测量。当电荷因电源形成的电场而移动时，就会产生电动势。

与基尔霍夫电压定律的结合

电动势与基尔霍夫定律相结合，有助于了解电源提供的能量和电路中各种元素（电阻器、电容器等）的能耗如何相互作用。电路各部分的电压降（负载的能耗）与电源提供的电动势相平衡。这种理解对于电路的设计、分析和故障排除来说非常重要。

【资料下载】活用Si(硅)功率器件特征的应用事例

为满足设备的节能和高效化要求，硅功率器件不断发展。本资料介绍从二极管、MOSFET的基础知识到选型方法以及最先进的元器件特性和应用案例。

下载