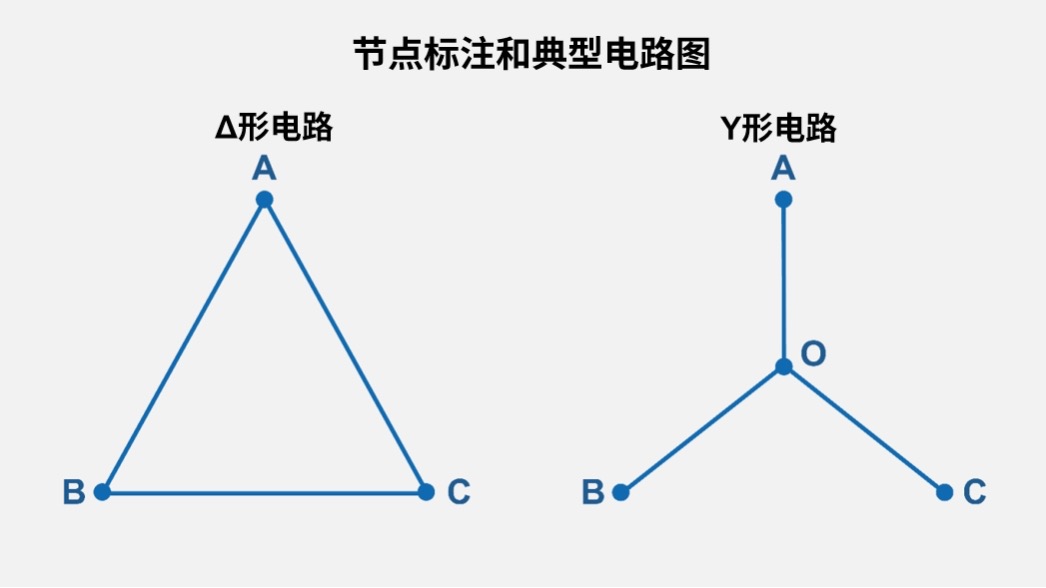
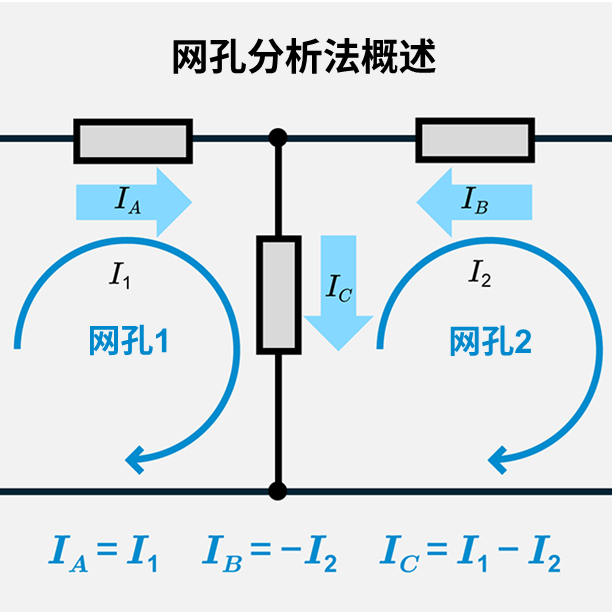
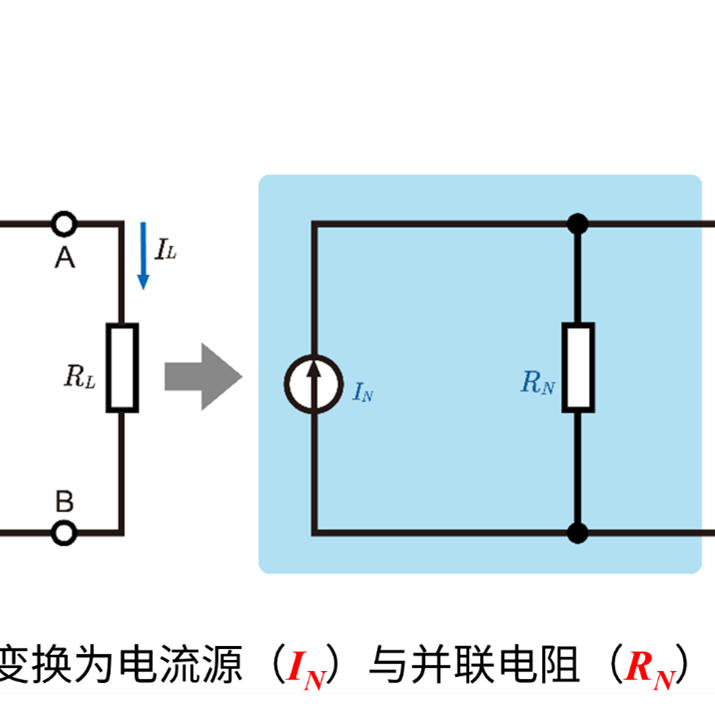
\(\)

什么是节点分析法？

节点分析法（节点电压法、节点电位法）是一种电路分析技术，以电路中各节点（连接点）的电位作为未知量，运用基尔霍夫电流定律（KCL）建立联立方程进行求解。作为与网孔分析法同样重要的经典电路分析方法，即使是包含众多电阻和电源的复杂电路，利用该方法也能准确求出各节点的电压。本文将详细阐述节点分析法的具体计算步骤。

节点分析法概述

节点分析法是将电路中各节点的电位作为未知量进行定义，并运用基尔霍夫电流定律（KCL）来表示流入和流出该节点的电流总和的分析方法。随着电路复杂程度的增加，逐个追踪各个电流和电压的难度也越来越大。通过聚焦于节点间的电位差，可将问题以联立方程的形式进行简洁明了的处理。在下图示例中，未知节点被设为“节点V”，并将其电位作为未知量处理。

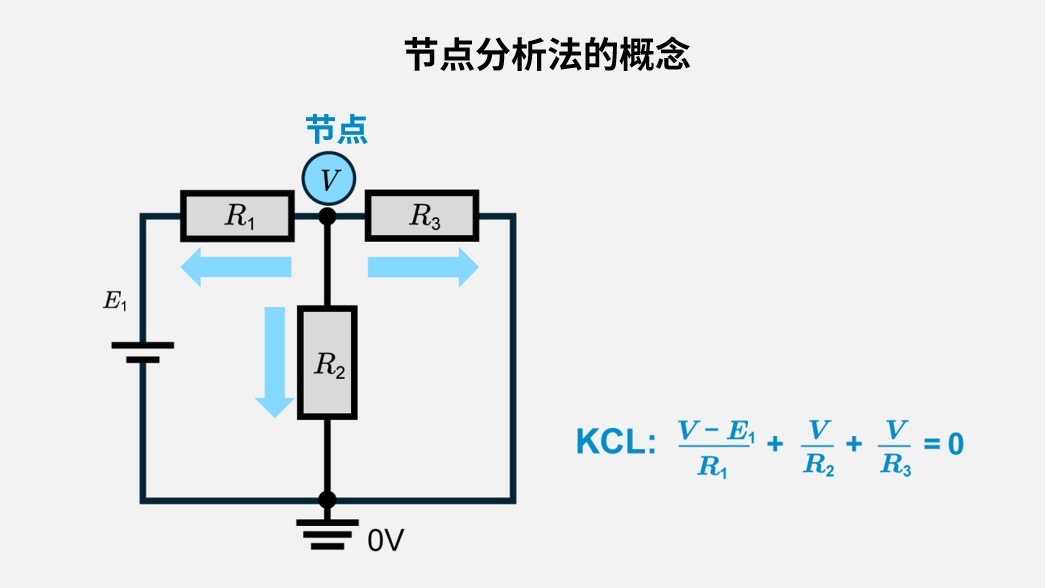
节点与参考节点（基准节点）

通常会选择电路中的任意一点作为参考节点（接地）。以该参考节点为参考点，将其他所有节点电压均定义为相对于该点的相对电位。由于未知量的数量等于“节点数减1”，因此即使电路规模庞大，也可有效缩减联立方程的规模。

节点分析法的理论基础

节点分析法主要结合基尔霍夫电流定律（KCL）和欧姆定律进行分析。KCL表明流入节点的电流总和等于流出节点的电流总和，而欧姆定律则揭示了电压与电流之间的线性关系。通过与这些定律相结合，为各节点建立方程并求解联立方程，即可完成整个电路的分析。

基尔霍夫电流定律（KCL）的应用

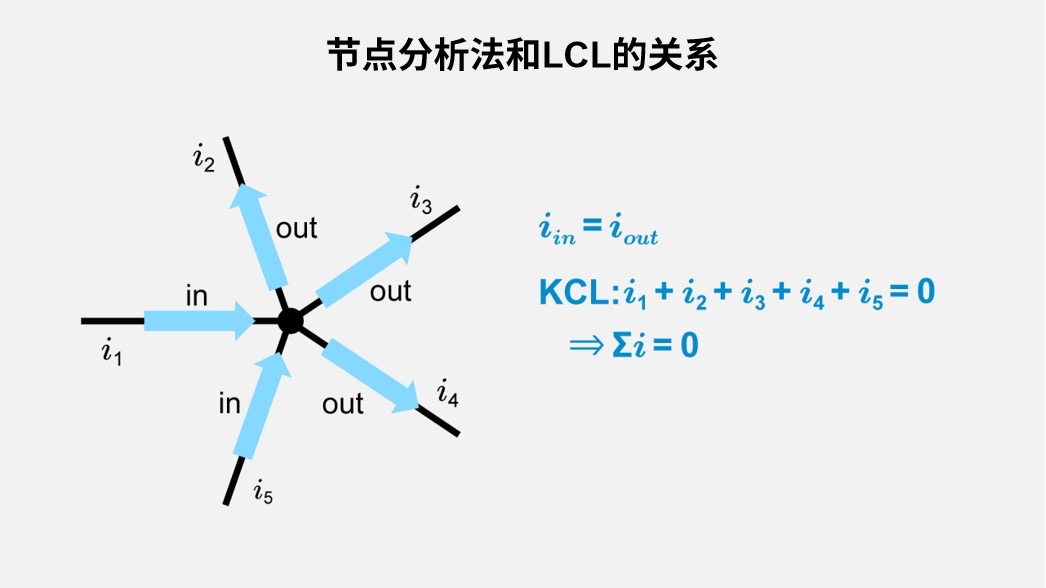
对于单一节点而言，流入该节点的电流总和与流出该节点的电流总和相等：

\(i_1+i_2+⋯+i_n=0\)

这是节点分析的基本方程。

欧姆定律与阻抗

各支路电流可由元器件两端的电位差除以电阻或阻抗来表示。

电阻R时：

\(i=\displaystyle\frac{(V_1-V_2)}{R}\)

同样地，电容和电感分别以频域中的阻抗\({jωL}\)和1/(\({jωC}\))来表示。

节点分析的基本步骤

下面是分阶段实施节点分析的步骤及注意事项。即使是大规模的复杂电路，只要按步骤进行，也可高效率地求解未知节点电压。本节将详细阐述采用矩阵形式（矩阵法）的计算过程（含中间步骤）。

第一步：选择参考节点

将电路中的一个节点设为参考节点（接地，0V）。通常，选择连接元器件最多的节点或实际电路中用作接地端子的节点，可减少未知量，使计算更简单。

参考节点选择要点

• 选择连接多个元器件（电阻、电源、负载等）的节点更容易建立方程。
• 在同时存在直流电（DC）和交流电（AC）的多电源混合电路中，可能有些复杂，但选择能使计算后的处理更简单的节点作为参考点更为有利。

第二步：定义节点电压

给参考节点以外的各节点分配电压\(V_1\), \(V_2\), …, \(V_n\)设总节点数为\(N\)时，未知量为（\(N\)−1）个。即使是大规模电路，也可明确变量的数量。

第三步：建立各节点的KCL方程

关于各节点

\(Σ\)(流入电流)\(=0\)

对于电阻和阻抗而言，均可运用欧姆定律来表示电流。

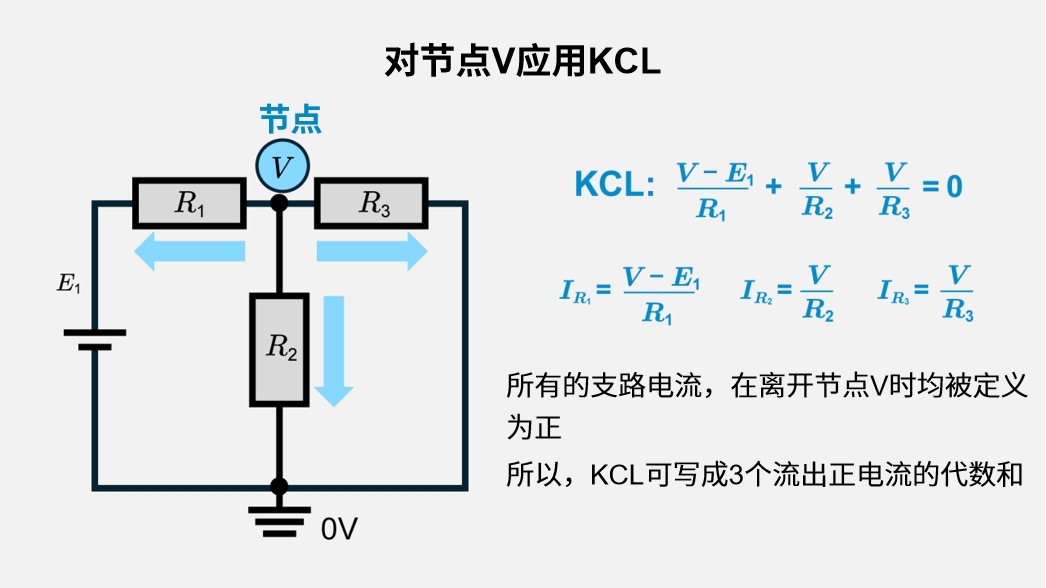
• 例如，节点\(V\)通过电阻\(R_1\)连接至电压源\(E_1\)（左侧节点），并进一步通过电阻\(R_2\)和\(R_3\)连接至参考节点\(G\)=0V时，针对节点\(V\)的KCL方程为：

  \(\displaystyle\frac{V-E_1}{R_1}+\displaystyle\frac{V}{R_2}+\displaystyle\frac{V}{R_3}=0\)

中间计算详细示例

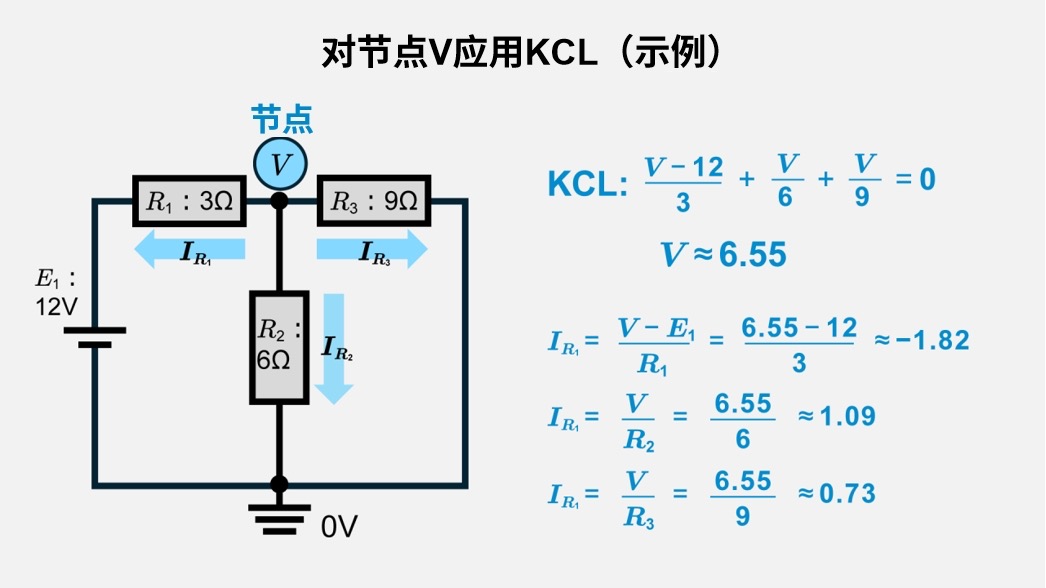
设\(R_1\)=3Ω、\(R_2\)=6Ω、\(R_3\)=9Ω、电压源\(E_1\)=12V、未知节点电压为\(V\)则

\(\displaystyle\frac{V-12}{3}+\displaystyle\frac{V}{6}+\displaystyle\frac{V}{9}=0\)

\(⟹V≈6.55V\)

在这里基于KCL得出的方程，也称为“节点方程（节点电压方程）”。当存在其他节点时，也可以同样地建立相应的方程，通过联立求解得出各节点的电位。

第四步：整理为矩阵形式并求解

将联立方程整理为导纳矩阵\(G\)与未知节点电压向量\(V\)的乘积\({GV}\) = \(I\)后，便可进行系统性处理。当未知量较多时，可采用计算机的联立线性方程组求解器（矩阵求解器），只要正确构建矩阵\(G\)即可通过\(V\)=\(G^{-1}\)\(I\)求解。

矩阵法示例

未知量中包含节点电压和部分电流时的步骤如下：

1. 将KCL、电压源的约束矩阵化
2. 通过逆矩阵或高斯消元法等直接的方法求解\({GV}\) = \(I\)

补充说明：对于电压源较多且回路数较少的平面电路，采用网孔分析法可能会使未知量更少。

超节点的处理

当两个非参考节点之间直接连接独立电压源时，仅靠常规的KCL方式是不够的。这种情况称为“超节点”，需要添加电压约束方程。

超节点的概念

在将电压源连接的两个节点视为一个“合成节点”并应用KCL时，需同时添加电压条件：\(V_1\)−\(V_2\)=电压源。

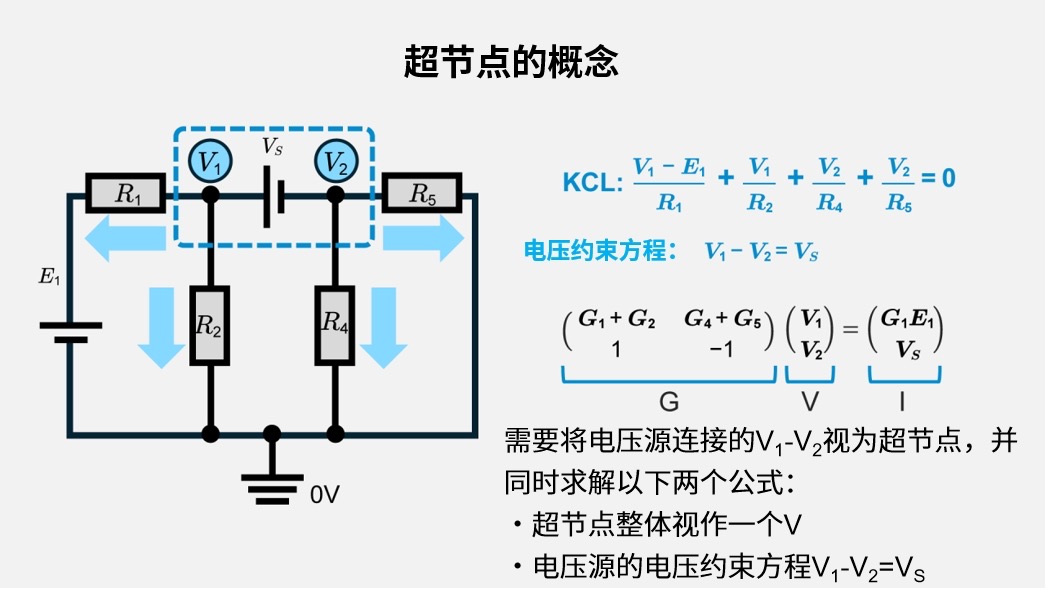
注意电压源的极性

• 如果将\(V_1\)−\(V_2\)=\(V_S\)或\(V_2\)−\(V_1\)=\(V_S\)处理错误，将会导致符号错误。

超节点方程和中间计算

例如，节点A和节点B通过电压源\(V_S\)相连，且各自对参考节点存在电阻时：

1. KCL（超节点整体）

   (\(V_1\)−0)/\(R_1\)+(\(V_2\)−0)/\(R_2\)+…=0

2. 电压约束

   \(V_1\)−\(V_2\)=\(V_S\)

将两者整合至\({GV}\) = \(I\)中。

节点分析法的实践案例

下面是一个使用代入了具体数值的电路、分步骤进行节点分析的示例。示例中也给出了在不省略中间计算步骤的情况下，同时将电流和节点电压纳入矩阵解的分析方法。

问题设定

求包含多个电压源和电阻的电路（如下图所示）中的节点电压\(V_1\), \(V_2\)与支路电流\(I_1\), \(I_3\)。

• 电压源（相对于0V参考节点）

  \(E_1\)=12V

• 电阻

  \(R_1\)=3Ω, \(R_2\)=6Ω, \(R_3\)=9Ω, \(R_4\)=12Ω, \(R_5\)=15Ω

具体示例（未知量的选定）

• 节点电压\(V_1\), \(V_2\)
• 支路电流\(I_1\), \(I_3\)

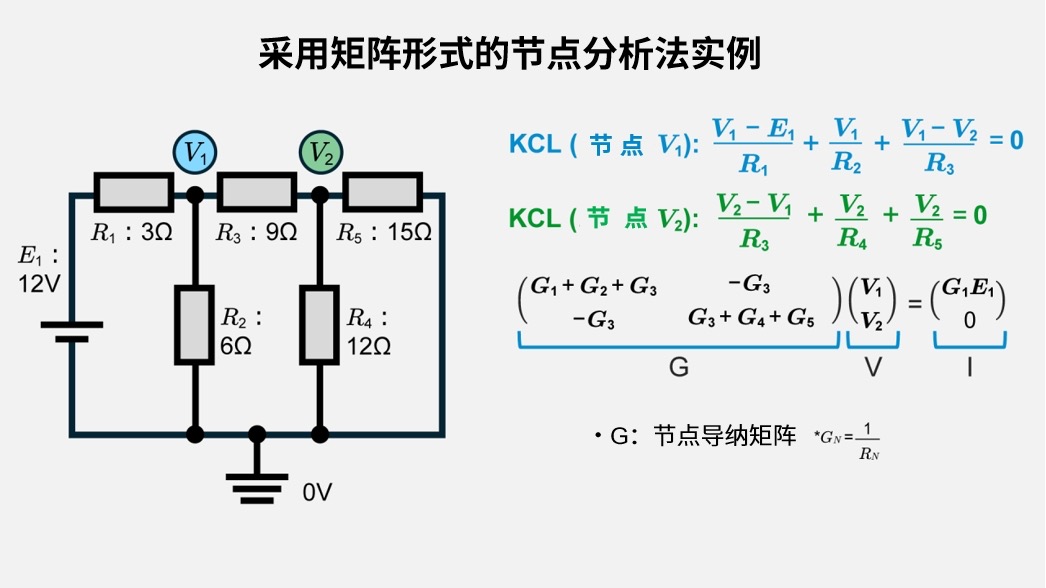
联立方程的构建

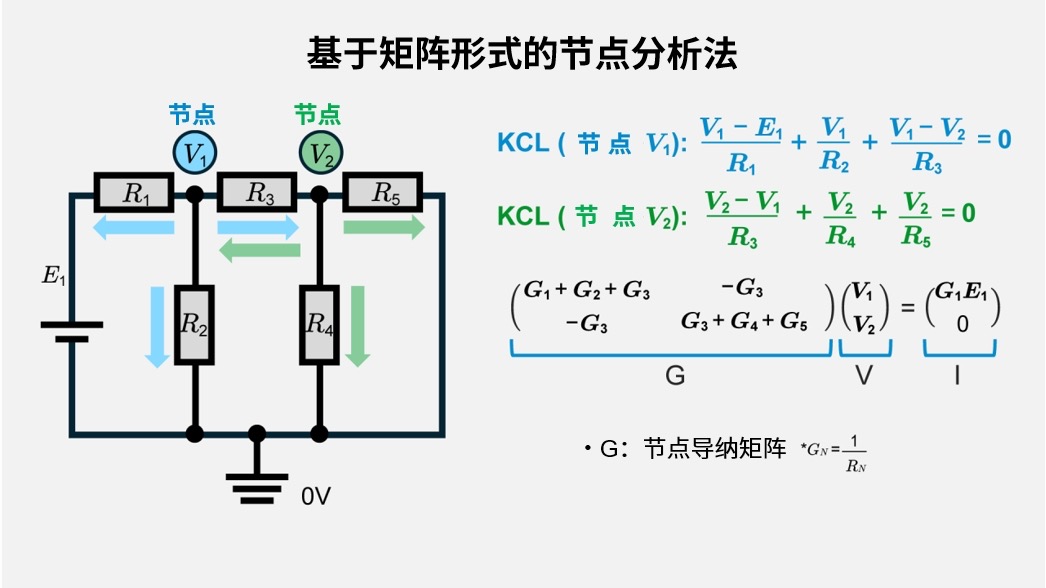
1. KCL（节点\(V_1\)）

   \(\displaystyle\frac{V_1-E_1}{R_1}+\displaystyle\frac{V_1}{R_2}+\displaystyle\frac{V_1-V_2}{R_3}=0\)

2. KCL（节点V₂）

   \(\displaystyle\frac{V_2-V_1}{R_3}+\displaystyle\frac{V_2}{R_4}+\displaystyle\frac{V_2}{R_5} =0\)

   构建GV = I

   \(G=\begin{pmatrix} G_1+G_2+G_3 & -G_3 \\ -G_3 & G_3+G_4+G_5 \end{pmatrix}, V=\begin{pmatrix} V_1 \\ V_2 \end{pmatrix}, I=\begin{pmatrix} G_1 E_1 \\ 0 \end{pmatrix}\)

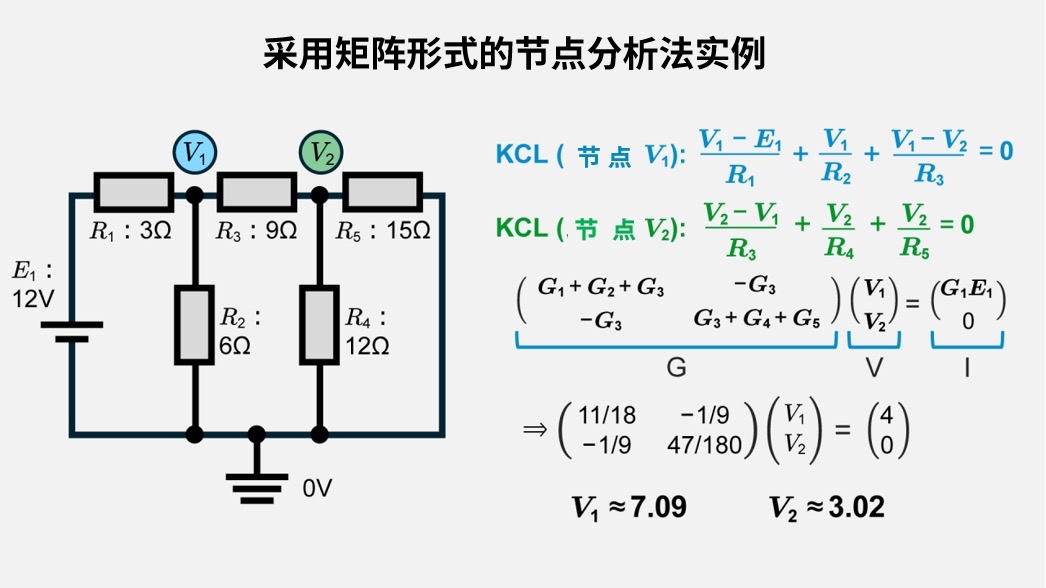
数值代入及计算

代入数值

\(G=\begin{pmatrix} \displaystyle\frac{11}{18} -\displaystyle\frac{1}{9} \\ -\displaystyle\frac{1}{9} \displaystyle\frac{47}{180} \end{pmatrix}, I=\begin{pmatrix} 4 \\ 0 \end{pmatrix}\)

\(V=G^{-1} I ⟹ V_1≈7.09 [V],V_2≈3.02 [V]\)

支路电流计算

\(I_1=\displaystyle\frac{E_1-V_1}{R_1} ≈1.64 [A],I_3=\displaystyle\frac{V_1-V_2}{R_3} ≈0.45 [A]\)

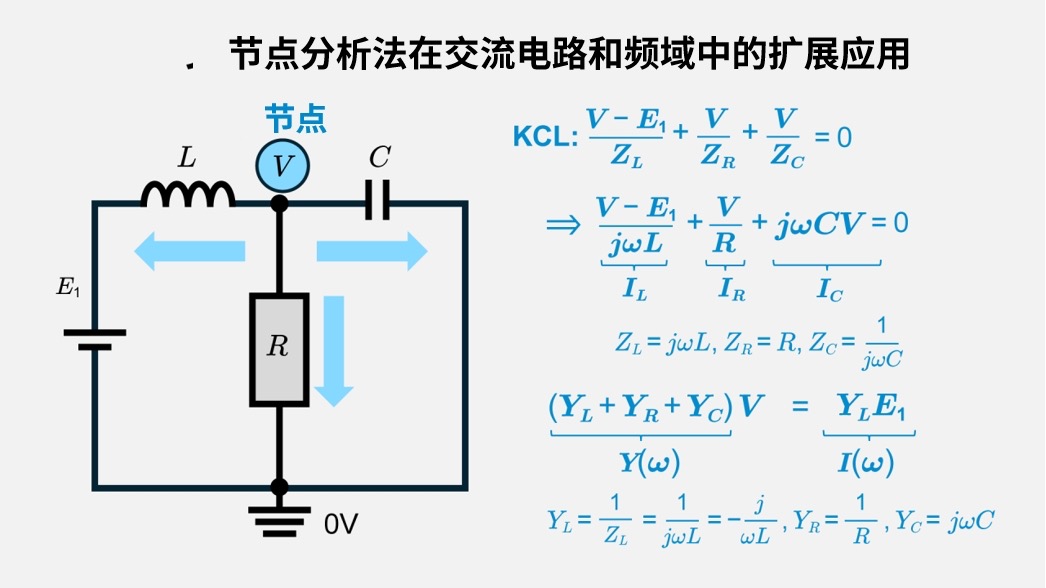
在交流电路和频域中的扩展应用

节点分析法不仅适用于直流电路，同样也适用于交流电路。在交流分析中，将电感和电容的频率依赖性作为阻抗\(Z\)来处理，并像直流分析一样建立节点方程。

• 电感\(L\)：\(Z_L\) = \({jωL}\)
• 电容\(C\)：\(Z_C\) = 1/(\({jωC}\))
• 阻抗\(R\)：\(Z_R\) = \(R\)

复数分析和矩阵形式

复数分析

在正弦波激励的情况下，各节点电压用复数表示，KCL用复数阻抗进行表述。其中，阻抗\(Z\)是指电阻、电感、电容等元件对交流电流呈现的频率依赖阻力。例如，阻抗\(Z\)所连接的节点电压\(V\)和\(V_X\)，其电流可表示为\(i\) = (\(V\) – \(V_X\))/\(Z\)。

最终可获得复数形式的节点电压。

频域的矩阵形式

1. 定义节点和参考节点
2. 确定各\(R\), \(L\), \(C\)
3. 以复数阻抗来表述KCL
4. 整理为\(Y\)(\(ω\))\(V\) = \(I\)(\(ω\))
5. 用复线性代数求解\(V\)通过扫描频率可获得伯德图等频率响应特性。

节点分析法在非线性大规模电路中的扩展应用

实际的电子电路中，包含多个受控源、二极管和晶体管等非线性元器件，甚至在IC芯片内部也存在数十万至数百万个节点。节点分析法作为一种通用的计算框架，可扩展应用于众多场景。

四种受控源的处理

受控源有四种类型：电压控制电压源（VCVS）、电流控制电压源（CCVS）、电压控制电流源（VCCS）、电流控制电流源（CCCS）。它们的输出取决于电路内部其他节点所测得的电压或电流。

• VCVS、CCVS（受控电压源）：在矩阵中添加电压约束行（CCVS需将控制电流\(I_X\)作为新变量导入）
• VCCS、CCCS（受控电流源）：在相应导纳项中添加系数（VCCS为\(g_m\)，CCCS为\(k\)等）

非线性元件的线性化与迭代解法

当电路中含有非线性元件时，\(I\)–\(V\) 特性将不再保持线性比例关系，此时节点方程将变为非线性联立方程。所以按照如下步骤

1. 假设工作点（初始偏置）
2. 在这一点上进行泰勒展开，仅采用一次项（线性化）
3. 通过牛顿迭代法等迭代解法进行解的更新

重复①〜③直至解收敛。这样，即使电路中含有非线性元件，每个步骤仍可按线性节点分析法进行处理。

在仿真工具中实装（SPICE等）

SPICE类仿真工具会在内部进行节点分析。

• 将各元件展开至节点导纳矩阵
• 自动执行上一节所述的线性化和迭代步骤
• 输出收敛后的节点电压和元件电流

用户只需绘制电路图，软件便会自动为各节点编号，并基于KCL求解方程。

半导体电路设计中的可扩展性

在IC中，虽然寄生电阻、电容和电感的存在会导致节点数量急剧增长，但方法论本身并无本质差异。

• 即使矩阵规模扩大，只要采用稀疏矩阵求解器或迭代预处理方法，仍可将计算量控制在线性至准线性范围内。
• 因此，在保持晶体管级详细模型的同时，可对整个芯片进行时序分析和电源完整性分析。

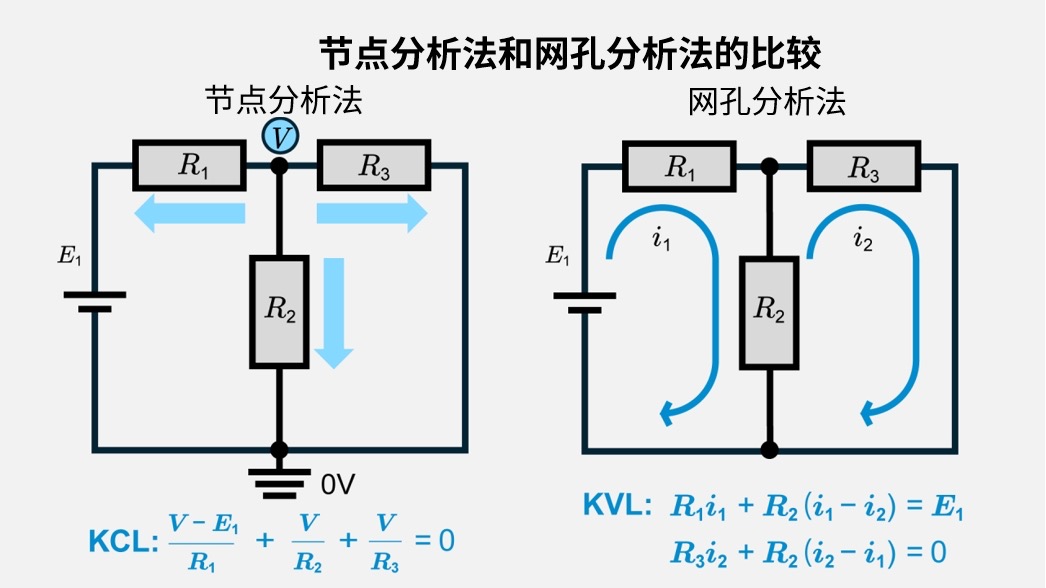
与网孔分析法的比较

另一种主要分析方法是网孔分析法（基于KVL、以回路电流为未知量），需根据电路结构和元件情况区分使用。

适用范围和选择指南

• 在回路较少的平面电路中，采用网孔分析法可以减少待求未知量，从而简化计算过程。
• 在电压源较多的电路或无法平面绘制的立体结构电路中，节点分析法往往步骤更为简洁且易于处理。
• 在元器件数量较多的大规模电路中，由于节点分析法可直接构建矩阵，因此即使电路规模扩大，计算时间也不会急剧增加，能够利用计算机进行高效处理。

在小规模电路的手工计算中，采用网孔分析法与节点分析法相结合的混合分析法同样行之有效。在这种混合分析法中，首先采用网孔分析法求解回路电流，然后利用该结果重新计算各节点的电位。通过先确定电流，可更轻松地处理仅凭节点分析法难以应对的电压源和公共电阻的影响，这一优势使得即便采用手工计算也很容易保持解的一致性。

结论

节点分析法是一种强大且系统化的电路分析方法。这种方法将各节点电压作为未知量处理，不仅适用于电阻电路，还适用于采用复数阻抗的交流分析，以及基于线性化、迭代法的非线性电路分析。通过施加约束条件，还可处理超节点等特殊情况。SPICE和众多仿真工具都是基于该原理构建的，是现代电子电路设计中不可或缺的分析方法。深入理解节点分析法，可从容应对大规模复杂电路。