网孔分析法（网孔电流法、回路电流法）是一种电路分析的基本方法，该方法将导线互不交叉的平面电路中的每个网孔电流设为未知量，并根据基尔霍夫电压定律（KVL）建立联立方程组，从而求解电压和电流。它是与节点分析法并列的代表性电路分析方法，尤其能够高效地求解具有多个电压源的电路。若能灵活运用这两种方法，就可以应对更广泛的电气网络。接下来我们将详细介绍网孔分析法的原理、基本步骤以及如何将其拓展应用于包含多个电源和受控源的复杂电路。

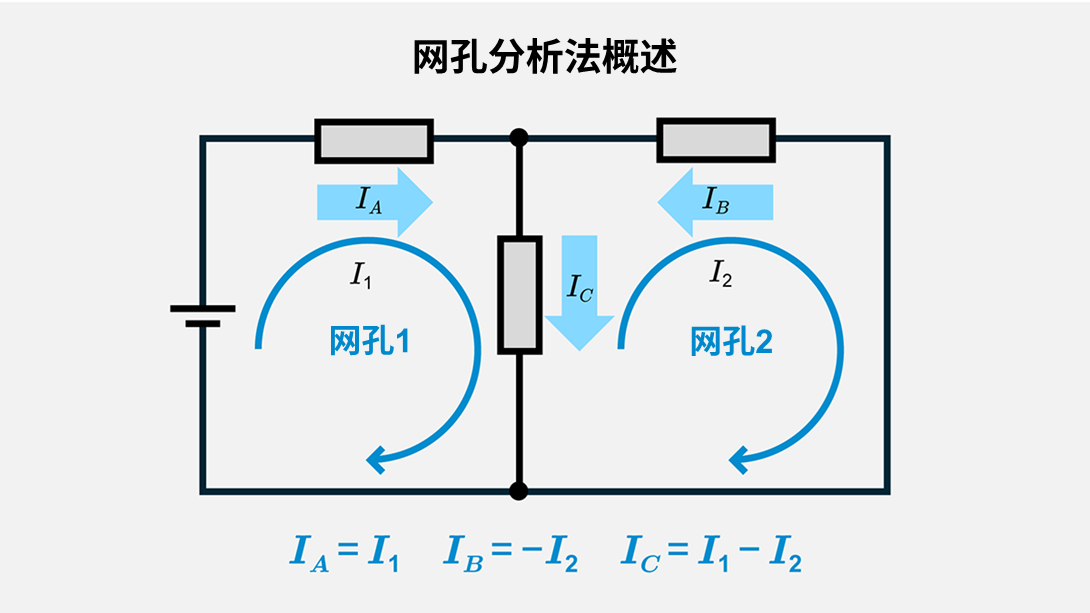
网孔分析法概述

网孔分析法的前提是目标电路为平面电路。该方法为每个闭合回路（即网孔）分配一个网孔电流作为未知量，并根据电路元件、电源和KVL建立联立方程组。由于大多数示例电路都是平面电路，因此该方法具有适用性强的特点。

与基尔霍夫定律的关系

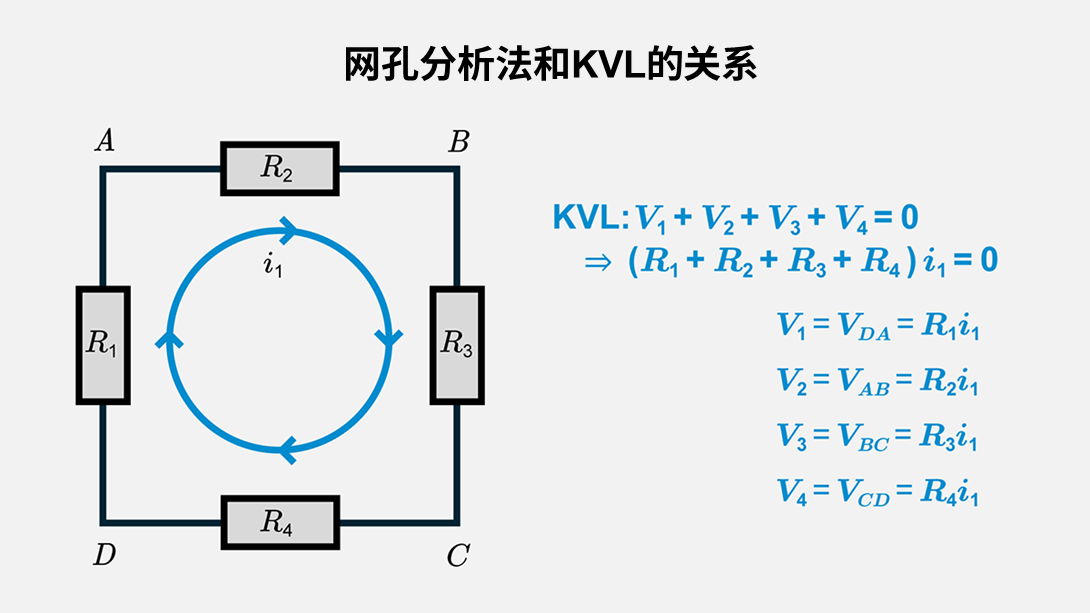
电路分析的基础是基尔霍夫电压定律（KVL）和基尔霍夫电流定律（KCL）。网孔分析法主要利用KVL来建立各回路的方程（回路电流方程）。对于每个独立的闭合路径（即网孔），通过网孔电流或网孔电流之差来表征电路元件上的电压降或电压升。另外，上图是一个不含电源的回路，仅用于展示KVL的列写方法，其中\(i_1\)=0是因为没有电源。在包含电源\(E\)的一般形式中，会变成\({R∑i}_1\)=\(E\)等形式，请注意后文示例中讨论的是包含电源的情况。例如，在双网孔电路中，若将网孔电流命名为\(I_1\)和\(I_2\)，那么对每个回路应用KVL，就可以得到两个联立方程组。

网孔分析法的优点和适用范围

网孔分析法的优点在于能够减少未知量的数量，尤其是在包含多个电压源的平面电路中。这种通过识别闭合回路来设置网孔电流的直观方法，在初学阶段或设计初期也是非常容易掌握的分析手段。

另一方面，对于立体布线等非平面电路，网孔的定义会变得困难甚至无法实现。这种情况下，采用节点分析法等其他方法更为合适。

基本步骤和示例

在网孔分析法中，需要定义围绕闭合回路流动的网孔电流，并对每个回路应用KVL。以下Step将采用仅包含电阻和电压源的简单案例来说明标准分析步骤。

Step 1：分配网孔电流

首先确认电路是平面电路，然后为每个基本网孔（不包含其他回路的最小闭合路径）设置任意方向的网孔电流。按照惯例，若将所有网孔均设为顺时针方向，会更易于进行符号管理。

Step 2：对每个网孔应用KVL

对每个网孔应用KVL，并用网孔电流表示每个元件的电压降或电压升。当网孔间共有元件时，该元件的电压用网孔电流的差值来表示。
针对每个网孔，沿着回路应用KVL。需注意电流是如何流过每个电路元件的，回路内有电压源时需注意其极性。当两个网孔共有一个电路元件时，需要用两个网孔电流在该元件内流动方向相反时的差值来表示该元件的电压降。

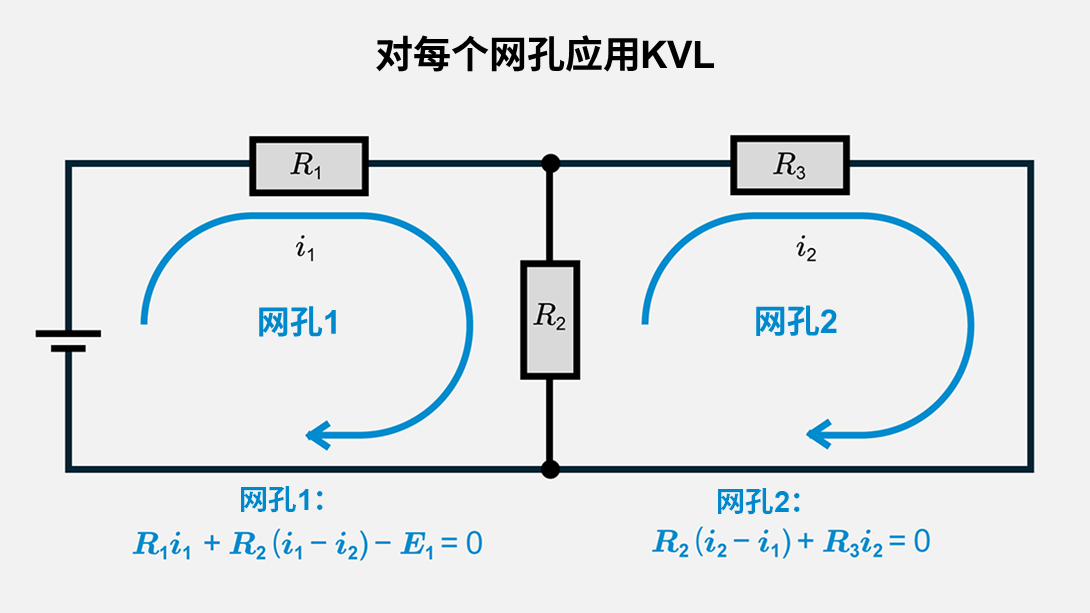
例如，考虑一个具有网孔电流\(I_1\)和\(I_2\)的双回路电路。假设第一个回路有电阻\(R_1\)、\(R_2\)和电压源\(E_1\)，第二个回路与第一个回路共有电阻\(R_2\)，并另含电阻\(R_3\)。对每个回路列写KVL，可以得到如下方程组：

\(R_1 i_1+R_2 (i_1-i_2 )-E_1=0\)

\(R_2 (i_2-i_1 )+R_3 i_2=0\)

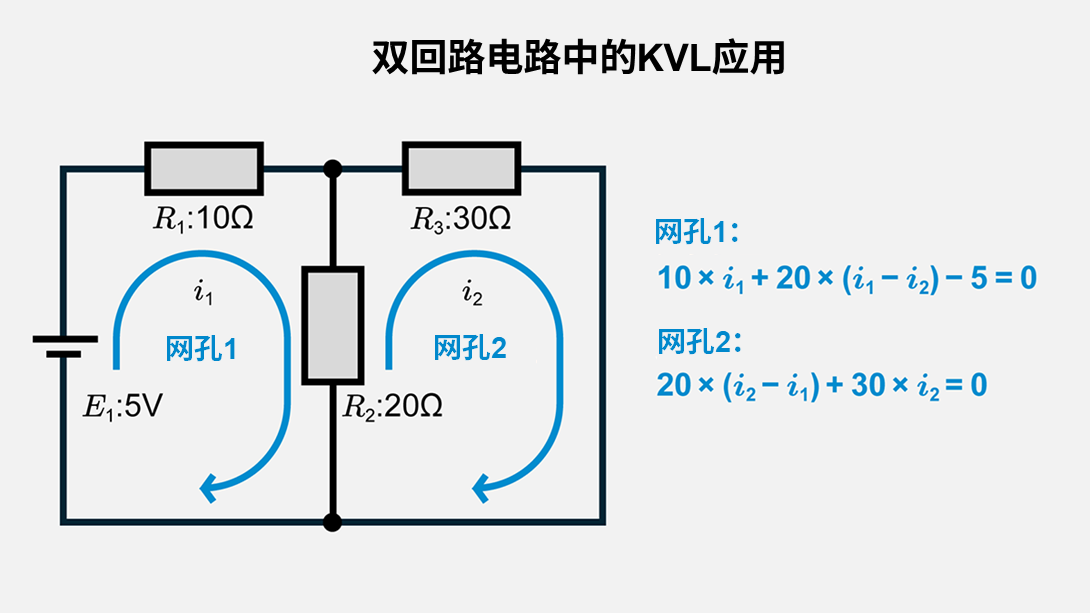
具体示例：双回路电路

• 网孔1：电阻\(R_1\)=10Ω，互电阻\(R_2\)=20Ω，电压源\(E_1\)=5V
• 网孔2：互电阻\(R_2\)=20Ω，电阻\(R_3\)=30Ω
• 将网孔电流\(i_1\)、\(i_2\)定义为顺时针方向

对网孔1应用KVL：

\(R_1 i_1+R_2 (i_1-i_2 )-E_1=0\)

代入数值：

\(10i_1+20(i_1-i_2 )-5=0⟹30i_1-20i_2=5\)（1）

对网孔2应用KVL：

\(R_2 (i_2-i_1 )+R_3 i_2=0\)

代入数值：

\(20(i_2-i_1 )+30i_2=0⟹-20i_1+50i_2=0\)（2）

Step 3：确认未知变量的数量

如果存在\(n\)个独立网孔，通常可以得到\(n\)个网孔电流和\(n\)个KVL方程。若存在受控源，需要补充约束关系方程组，并确认未知量数量与独立方程数量一致。

Step 4：求解联立方程组

求解示例
求解（1）（2）可得：

\(i_1≈0.23A,　i_2≈0.091A\)

互电阻\(R_2\)的电流为\(i_1\)−\(i_2\)≈0.14A，电压降约为2.73V。

对于小规模电路，采用代数消元法和代入法就足够了，但当网孔数量较多时，整合成矩阵形式并运用线性代数方法（或电路仿真器）求解会更高效。

基于矩阵形式的网孔分析法

当含有多个电压源或三个以上的回路时，手动求解所有的联立方程组将变得十分困难。在这种情况下，将方程组转换为矩阵形式，并应用标准的线性代数步骤（或电路仿真和软件），能够使分析更加系统化。下面将介绍网孔分析法中矩阵表达式的建立方法和求解步骤。

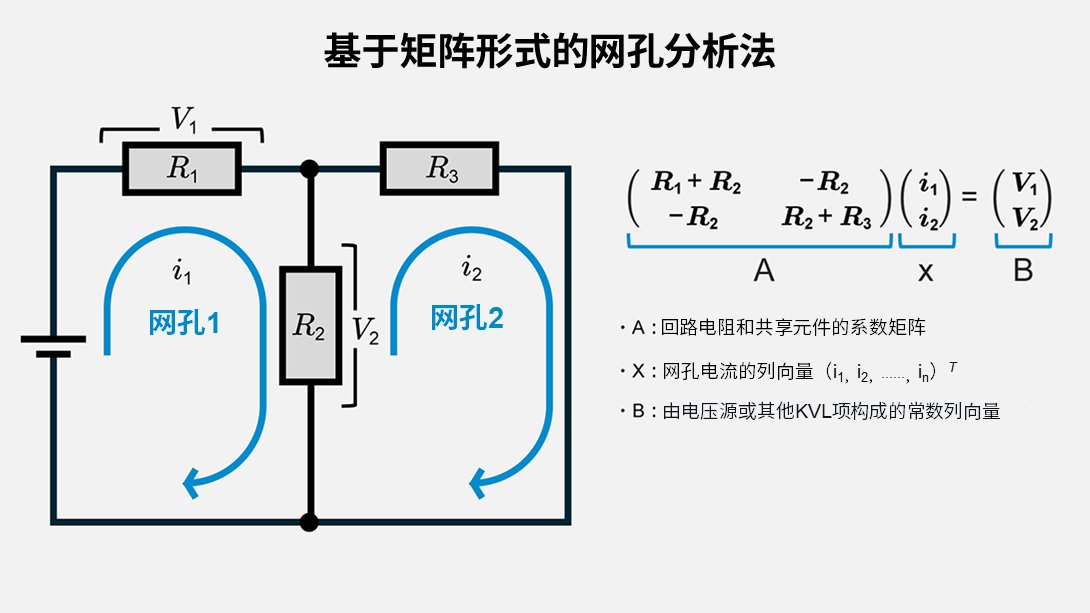
矩阵形式的建立

矩阵形式的通用形式如下：

\(Ax=B\)

• \(A\)：包含每个网孔的等效电阻和共有元件的系数矩阵
• \(x\)=(\(i_1\), \(i_2\), …, \(i_n\))\(^T\)：网孔电流向量
• \(B\)：电压源等常数项向量

在双网孔示例中，可以进行如下转换：

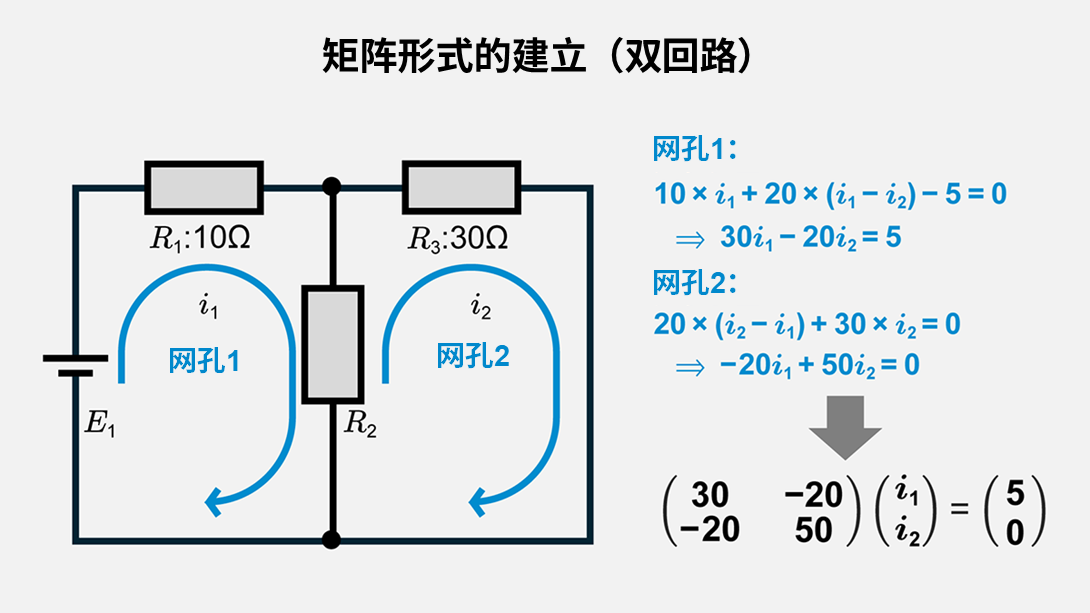
方程组：

\(30i_1-20i_2=5\)（1）

\(-20i_1+50i_2=0\)（2）

矩阵形式：

\(\begin{pmatrix} 30 & -20 \\ -20 & 50 \end{pmatrix}\begin{pmatrix} i_1 \\ i_2 \end{pmatrix}=\begin{pmatrix} 5 \\ 0 \end{pmatrix}\)

通用矩阵表达式\(A\)、\(X\)、\(B\)：

\(A=\begin{pmatrix} 30 & -20 \\ -20 & 50 \end{pmatrix}\), \(X=\begin{pmatrix} i_1 \\ i_2 \end{pmatrix}\), \(B=\begin{pmatrix} 5 \\ 0 \end{pmatrix}\)

1. 求\(A\)的矩阵方程：

   \(det(A)=30×50-(-20)×(-20)=1500-400=1100\)

2. 求\(A\)的逆矩阵（2×2较为容易）：

   \(A^{-1}=\displaystyle\frac{　1　}{1100} \begin{pmatrix} 50 & 20 \\ 20 & 30 \end{pmatrix}\)

3. 计算\(X\)=\(A^{−1}\)\(B\)：

   \(i_1≈0.23A,　i_2≈0.091A\)

结果与之前求得的解一致。

三回路以上的网孔分析法

对于具有特定共有元件和电压源的三回路电路，会生成一个可求解\(i_1\)、\(i_2\)、\(i_3\)的矩阵方程组。由此求出电路中任意支路的电流或电压降。

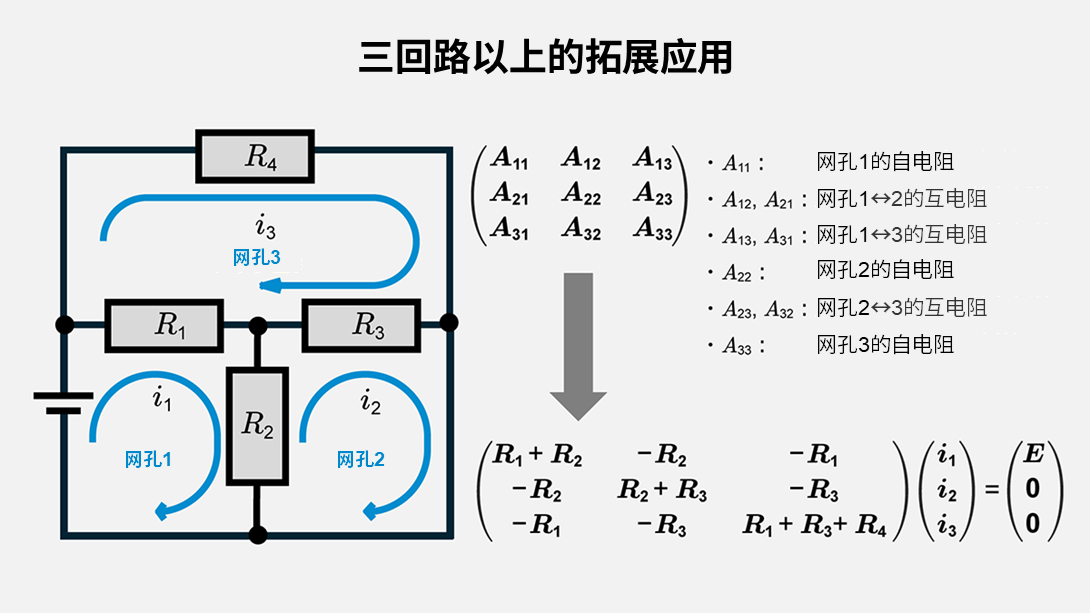
对于大规模或复杂的电路，使用电路仿真器等软件（MATLAB和Python等）处理会更为简便。可以根据具体情况选择更优的解法，如矩阵展开法或消元法等系统性的方法来求解。

交流电路中的拓展应用
只需将电阻\(R\)替换为复阻抗\(Z_R\)=\(R\)，电感\(L\)替换为\(Z_L\)=\({jωL}\)，电容\(C\)替换为\(Z_C\)=1/\({jωC}\)，即可用相同的矩阵表达式来求解频率响应。

超网孔的概念

当电流源等电路元件位于两个网孔的边界时，很难直接列写出这些网孔的KVL方程。在这种情况下，通常会采用超网孔分析法。超网孔是通过将两个网孔合并成一个避开电流源支路的大回路而形成的。当包含二极管和晶体管等非线性元件时，需利用在工作点线性化并每次更新回路矩阵直至收敛的方法（牛顿-拉夫逊法）等。

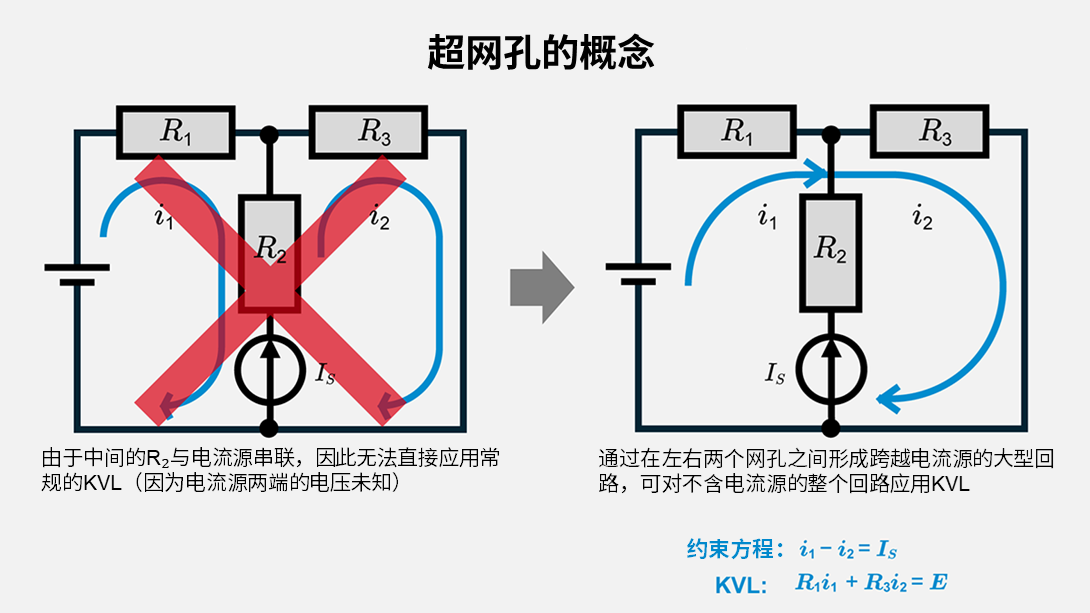
什么是超网孔

当电流源等元件位于两个回路之间时，就会出现这种情况。由于施加在该电流源上的电压降可能是未知的（不能通过简单的欧姆定律关系直接给出），因此需暂时将两个网孔视为一个不包含电流源支路的扩展回路，并围绕这个大闭合路径应用KVL。同时，补充一个与已知电流源\(I_S\)值相关的约束方程（示例中为\(I_S\)=\(i_1\)–\(i_2\)），从而求解未知电流。同样的思路可进一步扩展到多个电流源或受控电流源中。当因图示的需要而将其中一个网孔电流绘制成逆时针方向时，表达式可能呈现为\(i_1\)+\(i_2\)=\(I_S\)，但如果将\(i_2\)的方向统一后重新列写，该式将与\(i_1\)–\(i_2\)=±\(I_S\)完全等价。

超网孔的应用示例

假想网孔1和网孔2之间存在电流源\(I_S\)的情况，并定义网孔电流\(i_1\)和\(i_2\)。跳过电流源支路，创建一个合并了回路1和回路2的超网孔。针对这个超网孔列写一个KVL方程，并利用两个网孔电流的差值等于\(I_S\)这一关系，由此即可获得求解\(i_1\)和\(i_2\)所需的联立方程组。

含受控源电路中的应用

网孔分析法并不仅限于纯电阻电路或基于电压源的电路。只要电路保持平面结构，或者能够运用超网孔的概念进行处理，该方法也可适用于含独立电流源、受控电压源及受控电流源的电路。

独立电流源

当独立电流源完全位于回路内部时，改用节点分析法或采用其他方法处理该回路可能更为便捷。当电源被两个网孔共有时，通常需要采用超网孔分析法，或者也可以考虑能否通过节点分析法来减少未知量的数量。最终根据未知的网孔电流数量、回路方程的数量以及所需独立方程的数量来决定。

受控源

受控源有四种类型：电压控制电压源（VCVS）、电流控制电压源（CCVS）、电压控制电流源（VCCS）、电流控制电流源（CCCS）。在任何情况下，其输出都取决于电路中其他位置测量到的电压或电流。

• VCVS和CCVS（受控电压源）：在回路方程中补充\(α\)×\(i_x\)或\(β\)×\(v_x\)
• VCCS和CCCS（受控电流源）：补充超网孔或控制变量方程

这些关系需要明确地引入到联立方程组或矩阵形式中。这种方法虽然有效，但要注意符号规则和控制变量。

与节点分析法的比较

网孔电流分析和节点分析法经常会引发这样的疑问：“在什么情况下应该选用哪种方法？”。

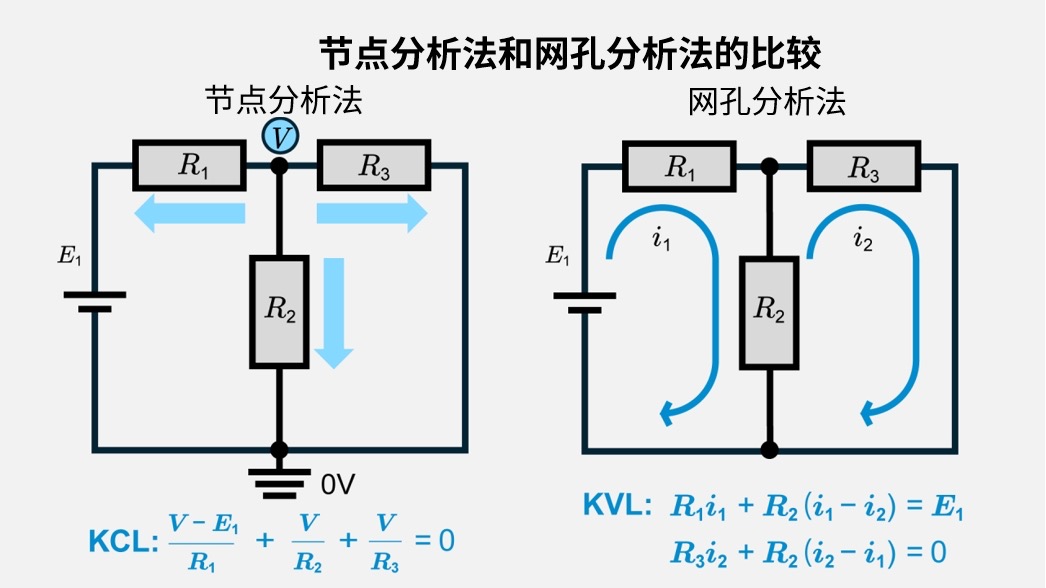
节点分析法基于基尔霍夫电流定律（KCL）来设定未知的节点电压，而网孔分析法则基于基尔霍夫电压定律（KVL）来设定未知的回路电流。
对于相同复杂度的电路，求解网孔电流方程通常比节点电压法所需的方程数量少。尤其是在电压源分布广泛且电路布局规整的平面电路情况下。

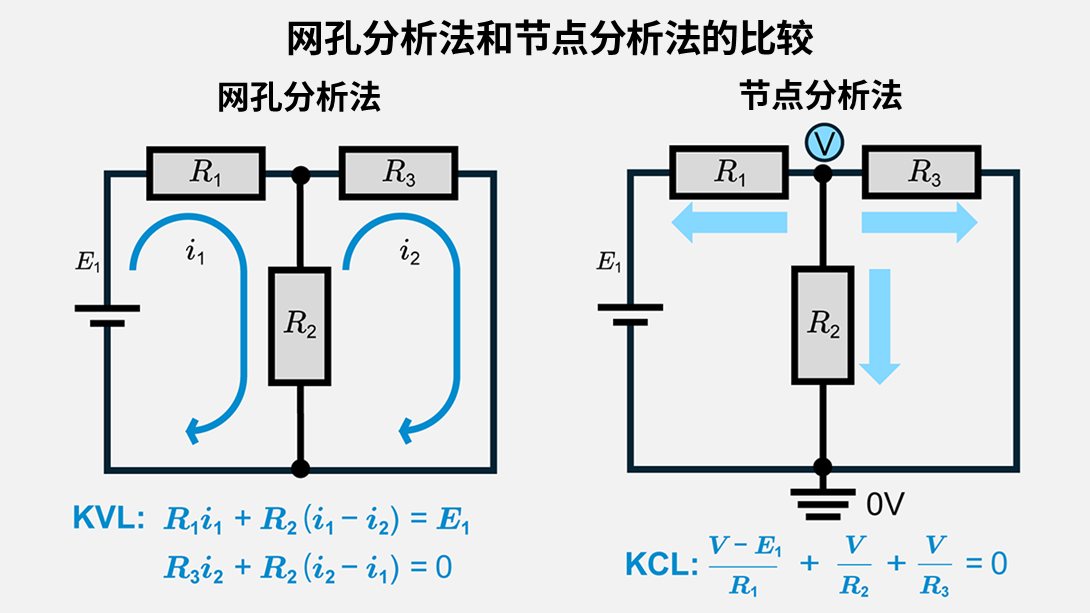
电源的类型、分布情况和判断标准

视角	网孔分析法	节点分析法
基础定律	KVL	KCL
未知变量变少的典型情况	含多个电压源的平面电路	含多个电流源的电路、非平面电路
难以应用的情况	非平面电路、含多个分布电流源	电压源串联连接较复杂的电路

• 电压源较多且为平面电路 → 宜采用网孔分析法
• 电流源分布广泛或非平面电路 → 宜采用节点分析法

这些指导原则并不是绝对的，选择网孔分析法还是节点分析法时，需要比较两种方法各自需要求解的未知量数量、电压源和电流源的分布情况以及电路是否为平面电路，从而确定更优方法。

总结

网孔分析法特别适用于导线互不交叉的平面电路，在以电压源为主的电路中，往往能够减少未知量的数量。采用矩阵形式后，即使是规模庞大或结构复杂的电路也能进行系统性地求解。另一方面，对于含多个电流源的电路或非平面电路，采用节点分析法等其他方法更为合适。通过同时掌握网孔分析法和节点分析法，可以大大拓宽从基础理论的学习到实际设计与仿真中电路分析的选择范围。