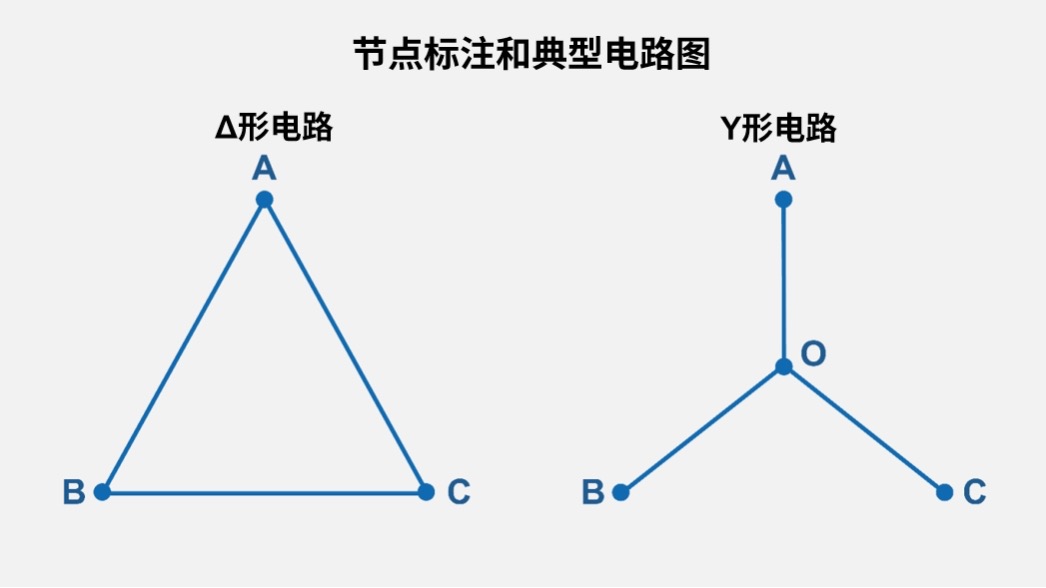
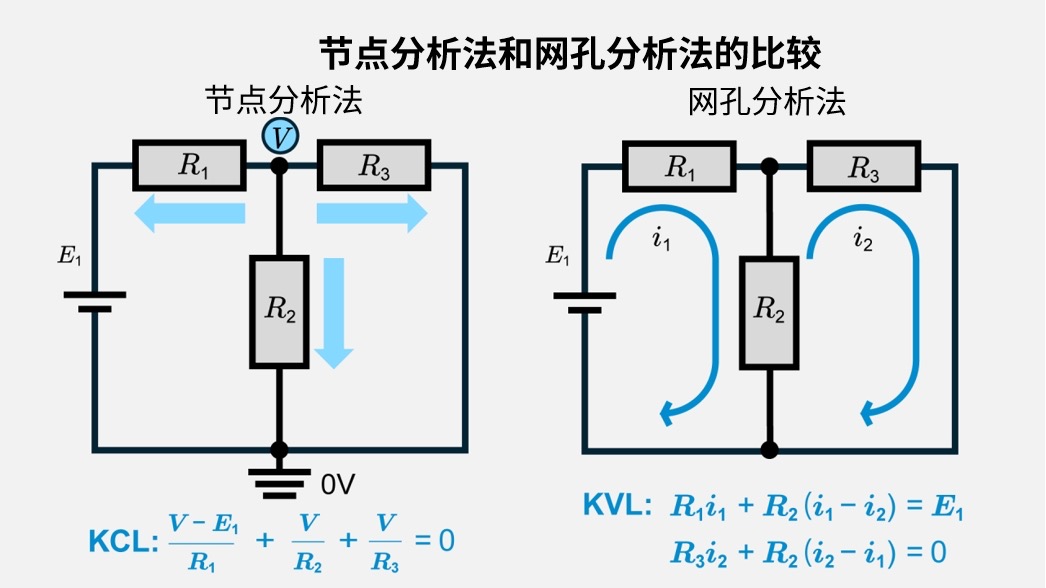
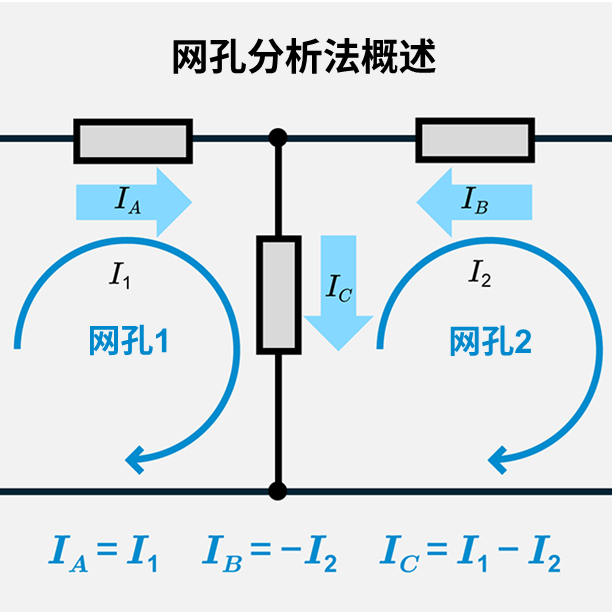
\(\)

诺顿定理：等效电路分析

诺顿定理是一种通过将复杂二端网络等效替换为电流源与并联电阻的组合来简化电路分析的方法。借助这种方法，即便在电路中包含电压源或受控电源的情况下，也能准确计算负载上的电流与电压，进而减少复杂电路设计的工作量。例如，诺顿定理的特点在于：在电路设计与学习场景中，不仅常用于对放大器输出特性的评估，还易于应用于滤波器及放大电路的优化工作。

本文将从诺顿定理的基本原理、具体求解方法，到与其他分析方法的区别，进行通俗易懂的介绍。同时，也将对诺顿定理的使用要点进行整理归纳。

诺顿定理的基本原理

诺顿定理指出：“从两个端子看进去的任意复杂线性电路，均可等效替换为一个电流源（\(I_N\)）与一个电阻（\(R_N\)）相并联的电路。”此外，诺顿定理的证明与戴维南定理呈表里一体的关系，二者可相互转换，这是其显著特征。

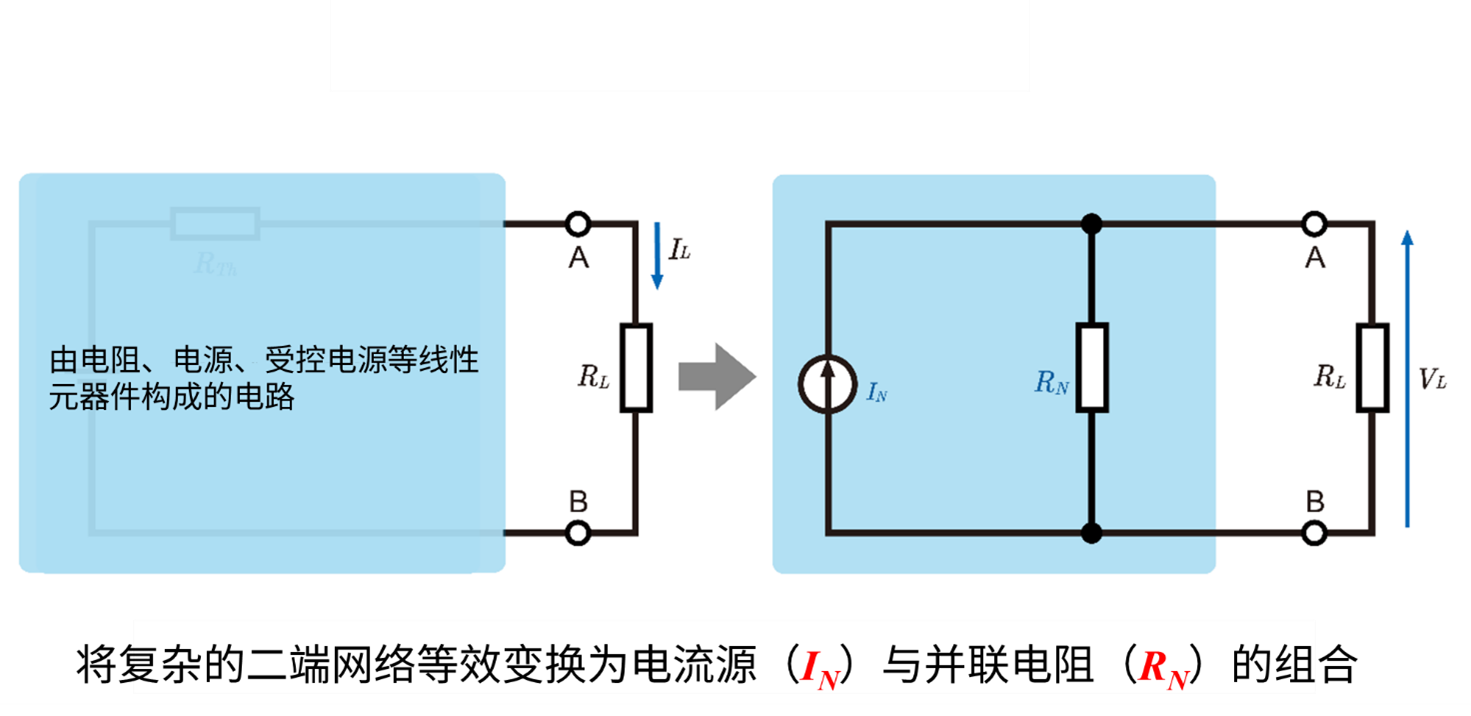
所谓“线性电路”，是指电压与电流的关系保持线性的电路，通常指包含电阻、线性独立电源、受控电源等元器件的电路。即使电路中包含二极管、晶体管等非线性元件，在特定工作点附近，有时也可通过采用线性化等效电路来应用，但本文将主要聚焦于线性元器件展开论述。

诺顿定理的优势之一在于，只需聚焦于连接负载的端子，即可将复杂的整个电路仅用两个元器件替换。最终，流过负载电阻的电流及端子间施加的电压的计算过程得以简化，为设计人员及学习者带来了便利。

构成诺顿等效电路的要素

要有效运用诺顿定理，必须准确理解构成其等效电路的要素。诺顿等效电路仅由两个元器件构成，即电流源与并联电阻（\(R_N\)）。掌握这一结构后，即便面对看似复杂的电路，也能快速把握其核心本质。下文将对诺顿定理中的核心要素——诺顿电流与诺顿电阻，以及它们之间的相互作用进行说明。

诺顿电流

应用诺顿定理时，最终可得到一个名为\(I_N\)的理想电流源。根据定义，\(I_N\)是将两个目标端子短接（直接连接）时流过的电流。

具体而言，需将负载电阻替换为理想导体，再通过计算或测量得出流入该导体的电流大小。

理想电流源的特性是无论端子电压如何变化，都会持续提供恒定的电流IN。实际电路元器件并不具备无限大的内阻，但通过这种理想化处理，不仅能简化电路计算过程，还能更清晰地把握电流源与负载之间的相互作用关系。

诺顿电阻

在诺顿定理的等效电路中，与电流源并联的元件是一个被称作\(R_N\)的电阻，即诺顿电阻。

求解\(R_N\)时，需先将电路中的所有独立电源进行置零处理（电压源短路、电流源开路），随后通过测量或计算，得出此时两个目标端子间的等效电阻值。若电路中存在受控电源，则需将其保留在电路中。这是因为受控电源的工作状态依赖于电路中其他部分的信号，无法像独立电源一样直接置零。

\(R_N\)是决定电流源与负载相互作用方式的重要要素。值得注意的是，可将\(R_N\)的倒数视为导纳（\(Y_N\) = 1/\(R_N\)），这种表述在进行并联电路变换时更为便捷。此外，部分文献还将\(R_N\)的倒数\(G_N\) = 1/\(R_N\)称为“诺顿电导”。在计算并联电路时，有时从电导角度分析会更方便，但从理论层面而言，无论是用\(R_N\)还是\(G_N\)，本质逻辑一致。从并联连接的角度来看，负载电阻与\(R_N\)呈并联关系，这一结构直接影响着负载电压与负载电流的计算结果。

诺顿等效电路概述

诺顿等效电路是由一个电流源（\(I_N\)）与一个电阻（\(R_N\)）并联构成，且这两个元器件的端子以与原电路的负载连接端子相对应的形式来呈现。

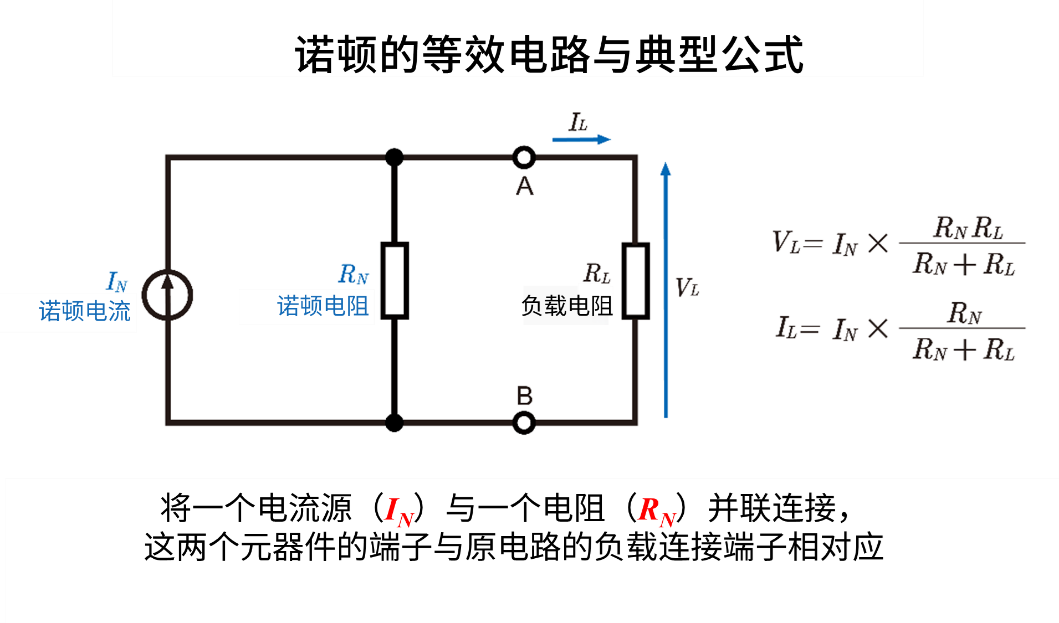
这一点与采用电压源\(V_{Th}\)和串联电阻\(R_{Th}\)的戴维南等效电路（结构上为串联形式）不同，但二者可相互转换。

诺顿定理的应用：诺顿电流与诺顿电阻的求解步骤

应用诺顿定理时，最重要的是掌握诺顿电流（\(I_N\)）与诺顿电阻（\(R_N\)）的计算方法。只要理解短路电流的求解方法，以及将电源置零后求解电阻的步骤，就能分析各类线性电路。下文将逐一说明这些步骤，并结合实例演示具体的计算方法。

诺顿电流的求解方法

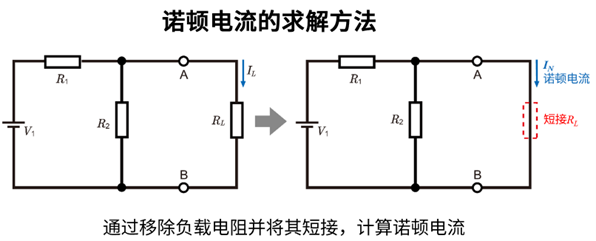
1. 将待分析电路的两个端子短接。
   即，将负载电阻\(R_L\)进行短接处理。
2. 通过电路方程或电路分析方法，求解该短接电路中流过的电流。
   可使用基尔霍夫定律（KCL、KVL）、欧姆定律、叠加定理等工具。
3. 该短接电流即为\(I_N\)。
   这一电流值将作为诺顿等效电路中理想电流源的参数值。若电路中存在多个电源，需将各电源向短接节点输送的电流相加，其总和即为诺顿电流。

・示例公式（单一电压源的场景）

假设有一个仅含电压源\(V_S\)、串联电阻\(R_S\)，并连接负载电阻\(R_L\)的简单电路。将\(R_L\)两端的端子短接时，产生的短接电流\(I_{SC}\)为：

\(I_{SC} = \displaystyle \frac{V_S}{R_S}\)

因此，

\(I_N=I_{SC}=\displaystyle \frac{V_S}{R_S}\)

可见，在“电路中仅含一个电压源和一个串联电阻”的场景下，短接电流可直接表示为\(V_S\)/\(R_S\)。但是，对于含多个电源或复杂电阻网络的电路，即便同样进行短接操作，分析步骤也会增加，此时需使用叠加定理求解最终的短接电流。

诺顿电阻的求解方法

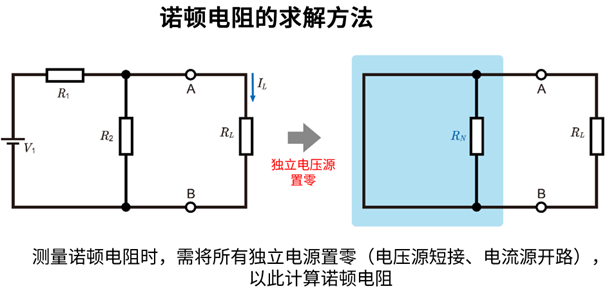
1. 将电路中的所有独立电源置零。
   电压源做短接处理，电流源做开路处理。
   若电路中存在受控电源，则需保留其在电路中。这是因为受控电源需根据电路的其他信号来工作。
2. 求解从这两个端子看进去的等效电阻。
   可通过对电阻进行串并联组合计算，或采用节点分析法来求解。
3. 求得的电阻即为\(R_N\)。
   该电阻便是诺顿等效电路中的并联电阻。

・示例公式

在前面提到的简单示例中，将电压源\(V_S\)短接后（此时电路中仅能看到\(R_S\)），从这两个端子间看到的电阻为：

\(R_N=R_S\)

即便面对更复杂的电阻网络，只要遵循上述步骤，通过进行电阻串并联等效计算及相关分析，即可求得最终的等效电阻值。

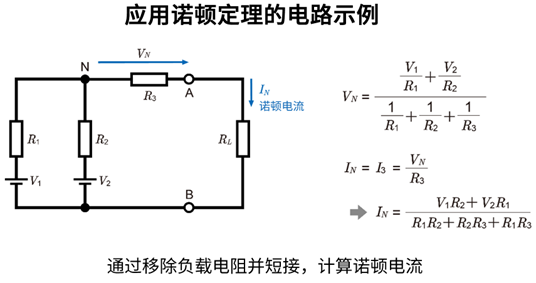
使用诺顿定理的电路解析例题

不仅要从概念上理解诺顿定理，了解其在实际计算与仿真中的应用方式也同样重要。本节将以包含多个电源与电阻的电路为例，逐步说明求解诺顿等效电路的步骤。通过这样的说明，大家在解析不同电压源、电流源及负载条件下的负载电阻电压时，思路将更加清晰。

电路解析例题

• 电源与内阻
  • 电压源\(V_1\)与电阻\(R_1\)串联连接，其负极连接至节点B
  • 电压源\(V_2\)与电阻\(R_2\)串联连接，其负极同样连接至节点B
• 节点N（上部连接点）
  • \(V_1\)・\(R_1\)与\(V_2\)・\(R_2\)的正极在节点N处汇合。
• 电阻\(R_3\)
  • 电阻\(R_3\)的一端连接节点N，另一端连接至节点A。
• 负载电阻\(R_L\)
  • \(R_L\)连接于节点A与节点B之间。
• 诺顿等效电路
  • 分析时，需先移除\(R_L\)，再针对移除后的A-B两个端子，求解其诺顿等效电路。

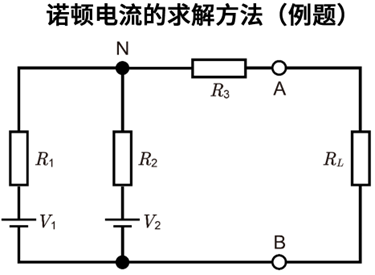
求解诺顿电流

1. 诺顿短接条件的设定

移除负载电阻\(R_L\)，将端子A–B完全短接。

此时端子A与基准节点B处于等电位状态，

电阻\(R_3\)成为连接节点N与基准节点B的独立电阻。

2. 求解诺顿电压\(V_N\)

设节点N的电位为\(V_N\)（V），并定义电流的正方向为“从N指向对应节点”，则各支路电流可表示为：

\(I_1=\displaystyle \frac{V_N-V_1}{R_1}, I_2=\displaystyle \frac{V_N-V_2}{R_2}, I_3=\displaystyle \frac{V_N-0}{R_3} =\displaystyle \frac{V_N}{R_3}\)

根据KCL（若电流正方向定义为“从N指向对应节点”，则\(∑\)流出=0），可得：

\(I_1+I_2+I_3=0\)

\(\displaystyle \frac{V_N-V_1}{R_1} + \displaystyle \frac{V_N-V_2}{R_2} + \displaystyle \frac{V_N}{R_3} = 0\)

整理后可得：

\(V_N \left(\displaystyle \frac{1}{R_1} + \displaystyle \frac{1}{R_2} + \displaystyle \frac{1}{R_3} \right) = \displaystyle \frac{V_1}{R_1} + \displaystyle \frac{V_2}{R_2}\)

\(V_N=\displaystyle \frac{ \displaystyle \frac{V_1}{R_1} + \displaystyle \frac{V_2}{R_2}}{\displaystyle \frac{1}{R_1} + \displaystyle \frac{1}{R_2} + \displaystyle \frac{1}{R_3}}\)

3. 求解诺顿电流\(I_N\)

短接电流\(I_N\)与流过电阻\(R_3\)的电流相等，即：

\(I_N=I_3=\displaystyle \frac{V_N}{R_3} = \displaystyle \frac{\displaystyle \frac{V_1}{R_1} + \displaystyle \frac{V_2}{R_2}}{R_3 \left(\displaystyle \frac{1}{R_1} + \displaystyle \frac{1}{R_2} + \displaystyle \frac{1}{R_3} \right)}\)

对分母进行整理后可得：

\(I_N=\displaystyle \frac{V_1 R_2+V_2 R_1}{R_1 R_2+R_2 R_3+R_1 R_3}\)

・电流的正方向为从节点N指向端子B。

・若带有负号，则表明实际电流方向与正方向相反（即从 B指向A的方向）。

4. 使用注意事项

当接入任意负载电阻\(R_L\)时，可利用诺顿电流\(I_N\)及从端子A–B看进去的等效电阻\(R_N\)(= \(R_{Th}\)) = \(R_3\) + (\(R_1\)‖\(R_2\))进行计算（计算时需将独立电源置零，即电压源短接、电流源开路）。通过诺顿-戴维南转换，可便捷计算出电流与电压的分配关系。

求解诺顿电阻

求解\(R_N\)时，需先将独立电源\(V_1\)与\(V_2\)置零（电压源做短接处理，电流源做开路处理）。再求解从连接负载电阻\(R_L\)的端子看进去的等效电阻。

• 当\(V_1\)短接后，\(R_1\)的一端将接地。
• 当\(V_2\)短接后，\(R_2\)的一端将接地。
• 确认\(R_3\)是如何接地的。

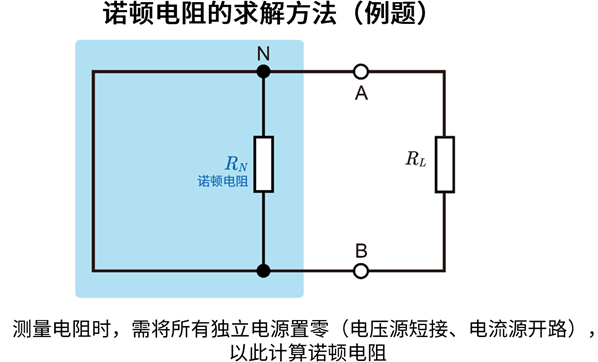
仔细梳理电路的连接状态，就能判断出\(R_1\)与\(R_2\)是否为并联关系，或是\(R_3\)与它们以串并联的方式组合。最终合成的电阻值即为\(R_N\)。若求得\(I_N\)与\(R_N\)，诺顿等效电路可直接表示为

\(I_N || R_N\)

的形式。

诺顿定理与戴维南定理的比较

与诺顿定理并列，戴维南定理是电路简化的主要方法。直观上二者呈现出不同的形式，实则存在密切关联。本节将明确诺顿等效电路与戴维南等效电路的对应关系，并探讨不同场景下哪种定理的应用更便捷。

诺顿定理与戴维南定理的关系

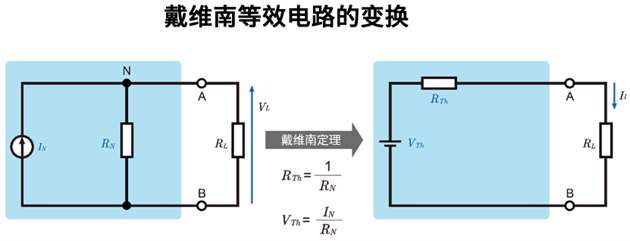
戴维南定理指出：“任何线性二端网络，都可通过一个电压源\(V_{Th}\)与串联电阻\(R_{Th}\)进行等效替换”。而诺顿定理则是将同一网络用电流源\(I_N\)与并联电阻\(R_N\)来表示。两者的关系可表示为：

\(I_N=\displaystyle \frac{V_{Th}}{R_{Th}} , R_N=R_{Th}\)

理论上，\(R_{Th}\) ＝ \(R_N\)。无论电阻的具体合成形式是并联、串联还是其他复杂组合，诺顿电阻与戴维南电阻在最终数值上都是相等的。

定理选择的判断要点

两种定理均有助于简化电路，但根据电路的具体情况，其中一种可能更直观易用。

• 戴维南形式：电流源（\(V_{Th}\)）+ 串联电阻（\(R_{Th}\)）
  • 适用于关注电压或功率的场景。
  • 便于观察负载变化时电压的变化规律。
• 诺顿形式：电流源（\(I_N\)） + 并联电阻（\(R_N\)）
  • 适合分析电流的分流情况。
  • 可简化含多个并联连接的电路分析。

电路的布局不同，哪种形式更易于自然处理也会有所不同。

含受控电源或交流元件的电路中的诺顿定理

在实际设计及研究级别的电路中，往往包含受控电源或交流元件。即便如此，只要电路保持线性，诺顿定理仍然适用。以下将说明在含受控电源或受频率影响的元器件的电路中，应用诺顿定理时的注意事项。

含受控电源的场景

受控电源（又称受控源）是一种电压源或电流源，其数值由电路中其他电气量决定。只要整个电路保持线性，诺顿定理即可适用，但即使在将独立电源置零时，也需保留受控电源。

受控电源无法从电路中完全移除。需在保留控制方程的前提下，计算\(I_N\)和\(R_N\)。

频率成分

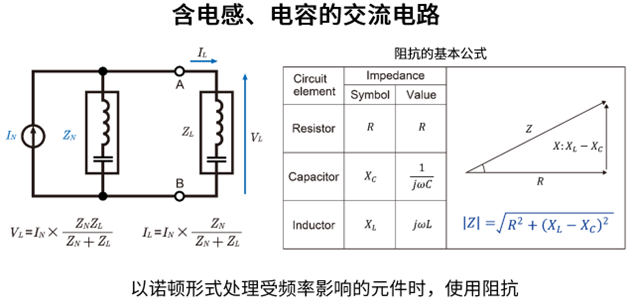
当电路中包含电容或电感时，其阻抗特性会随频率变化而不同。要将诺顿定理扩展应用于交流分析，需将每个电容和电感表示为复阻抗形式。

例如，

\(Z_C=\displaystyle \frac{1}{jωC} , Z_L=jωL\)

如此表示后，即可在复数域中对电路进行分析。求解短接电流的步骤以及电源置零的操作，除需采用复数进行计算外，本质上相同。

诺顿定理的应用：最大功率传输与负载调整

诺顿定理不仅能简化电路形式，还可用于评估负载条件变化时的功率传输、负载电流计算等场景。特别是众所周知的最大功率传输问题，借助诺顿等效有时能直观理解。本节将说明诺顿形式在优化负载条件、计算功率时的作用机制。

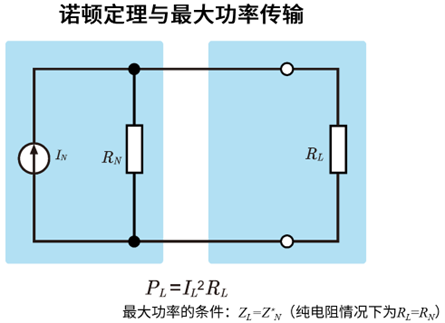
最大功率传输的条件

最大功率向负载传输的条件是：在交流（复阻抗）的一般情况下，负载阻抗需等于等效输出阻抗的复共轭，即\(Z_L\)=\(Z^{*}\)\(_N\)（同时满足\(R_L\)=\(R_N\), \(X_L\)=−\(X_N\)）。若限定为直流（纯电阻），该条件可简化为\(R_L\)=\(R_N\) 。

设计中若能选择或调整\(R_L\)=，使用诺顿等效有时能简化分析。例如放大器的输出级等场景，通过匹配负载与输出阻抗以追求最大效率的情况，就是典型应用。

快速评估负载电流的变化

若已知\(I_N\)和\(R_N\)，就能轻松掌握负载电阻\(R_L\)变化时负载电流的变化规律。

\(I_L=\displaystyle \frac{I_N×R_N}{R_N+R_L}\)

这相当于并联电路中的电流分流规律，而负载电压可通过以下公式计算：

\(V_L =I_L ×R_L\)

使用戴维南形式也能完成相同计算，但当分析重点放在电流分流时，诺顿形式往往更简便快捷。

与诺顿定理相关的拓展主题

掌握诺顿定理后，在实际应用中，将其与其他原理或定理结合使用十分重要。尤其对于包含多个电源或复杂连接的电路，利用弥尔曼定理或叠加定理，可逐步分解问题。本节将介绍几个与诺顿定理密切相关的拓展主题，以进一步深化理解。

诺顿定理与弥尔曼定理的关系

弥尔曼定理是用于求解多个带内部电阻的电压源并联时合成电压的定理。在应用诺顿定理的过程中，也会频繁出现对并联连接的电流源及内部电阻进行合成的计算。这与弥尔曼定理所采用的形式化分析方法非常相似。

诺顿定理与叠加定理的结合

如前所述，求解诺顿电流（\(I_N\)）时，若电路中存在多个独立电源，通常会用到叠加定理。单独考虑每个电源并求解短接电流，再将这些电流相加即可得到IN。这种方法在小规模电路中虽略显繁琐，但步骤明确，且与诺顿定理的兼容性良好。

非线性元件的近似分析

本文此前均以线性电路为前提，但实际的半导体电路中通常包含非线性元件。即便如此，若在工作点附近对电路进行线性化处理，仍可利用诺顿等效进行近似分析。例如，可将晶体管的基极-发射极结视为二极管求解小信号阻抗，并将集电极电流作为受控电源处理，诸如此类的方法均适用。

但如果处理的是跨越工作点、涉及多个工作区域的大振幅信号，直接应用诺顿定理会比较困难。这种情况下，仿真或数值分析是主流方法。

总结

截至目前，本文已介绍了诺顿定理的基本概念、等效电路的推导方法、与戴维南定理的关系，以及在更复杂场景下的应用等内容。最后，我们将聚焦诺顿定理的实用公式，整理其核心要点如下：

• 诺顿定理的公式
  • \(I_N\)：将端子短接时的短接电流（\(I_N\) = \(I_{SC}\)）
  • \(R_N\)：将独立电源置零时，从端子间看到的电阻
    负载电流：\(I_L\) = \(I_N\)×\(R_N\) / (\(R_N\)+ \(R_L\))
    负载电压：\(V_L\) = \(I_N\)×(\(R_N\)×\(R_L\)) / (\(R_N\)+\(R_L\))
• 最大功率传输与负载调整
  • 最大功率传输条件（直流电阻场景）：
    当\(R_L\) = \(R_N\)时，负载可获得最大功率（交流电路中条件为\(Z_L\) = \(Z^{*}\)\(_N\)）
• 与戴维南定理的关系
  • 换算公式：\(V_{Th}\) = \(I_N\)×\(R_N\) , \(R_{Th}\)= \(R_N\)
• 与叠加定理、节点分析的结合应用
  • 电路中存在多个电源时，利用叠加定理可更便捷地求解短接电流
• 可应用于含受控电源或交流元件的电路（前提是保持线性）
  • 分析时需保留受控电源，不可移除
  • 交流元件需以复阻抗形式处理

诺顿定理是与戴维南定理并列的电路分析基础方法。

即便对于包含多个电源或负载的复杂电路，只要掌握诺顿定理的应用方法，就能更清晰地掌握电路中的电压和电流规律。希望大家能在今后的电路设计与学习中灵活运用。