无刷电机：正弦波驱动的转矩脉动

我们目前正在探讨正弦波驱动，之所以谈这个主题，是因为当初谈及正弦波驱动是不会产生像120度驱动时的那种转矩脉动的驱动方式之一。在本主题中，我们来了解与120度驱动相同过程中的正弦波驱动时的转矩脉动。转矩的计算公式与120度驱动相同，见下图：

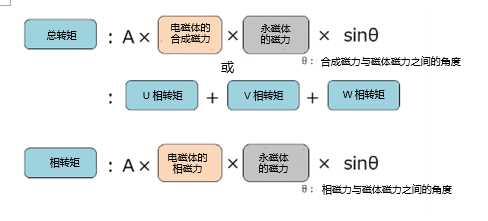
先来了解一下相转矩。由于流经U相绕组的电流呈正弦波状，因此U相电磁体的磁力也随之发生变化。根据其与转子（永磁体）的位置关系θ求出sinθ，计算U相的转矩，得到下图所示的正弦波形状。这个正弦波是周期为1/2、整体升高的波形（中点不是零，最低点接近零）。

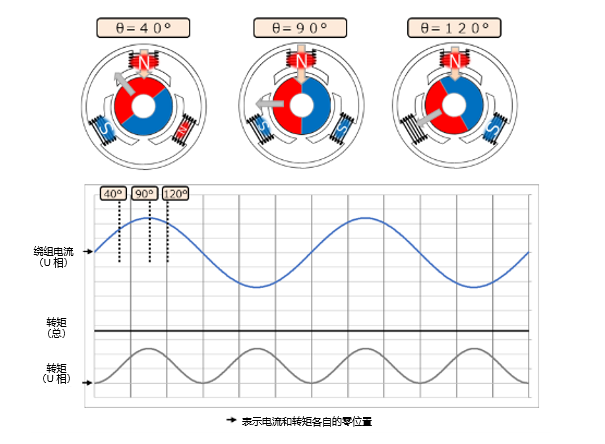
在正弦波驱动中，如果只看某一相的转矩，也会呈现这样的脉动。但是，如果将三相加在一起，总转矩就是恒定的。通过“角度互差120度的三个正弦波相加等于零”这一点即可理解。变为正弦波状的部分变为零，只有各相提升的部分相加，成为恒定转矩。

相转矩 = A•磁力(=电流)•sin(θ)
=A•sin(θ)•sin(θ)
=A•(−12(cos(θ+θ)–cos(θ−θ)))
=−A2(cos(2θ)+A2
→sin(2θ)+B

*关于“→”行

・由于cos和sin的区分并不重要，所以用sin2θ代替。
・-A/2在这里也不重要，所以删除
・用B替换A/2

总转矩：总转矩=U转矩+V转矩+W转矩
=(sin(2θ)+B)+(sin(2(θ+120))+B)+(sin(2(θ+240))+B)
=sin(2θ)+sin(2(θ+120))+sin(2(θ+240))+3B
=sin(2θ)+sin(2θ+240)+sin(2θ+480)+3B
=sin(2θ)+(−12sin(2θ))+(−3√2cos(2θ))+(−12sin(2θ))+3√2cos(2θ)+3B
=3B

在“正弦波驱动（正弦波激励）”一文中，我们提到过只要三相绕组合成磁场与转子保持一定大小的角度旋转，转矩脉动就会消失。可见，该转矩脉动变为零这一情况，通过上述过程也可以实现。

还有，这里关于绕组电流的相位，按照在绕组电流的峰值位置与转子间的相对角度θ为90度、当电流为零时θ为0度或180度来计算转矩。这是因为与120度驱动时相同，前提是假设在绕组引脚上施加了能够使转子磁体所在位置产生这样电流的电压。那么，如果角度偏离该位置会怎样呢？

无刷电机：正弦电流的时序

前文提到的正弦电流的相位是与磁体间角度为90度时正弦电流峰值所在位置的相位。当角度偏离该位置时，转矩会如何变化呢？下面我们来确认一下变化情况。

前提条件是U、V、W相的绕组电流的相位都统一变化。这样，各相之间就会保持120度的角度偏差。

接下来，我们用与前文一样的方法来计算相转矩。假设电流相位偏移C度，那么通过下列公式可以看出转矩提升量会变化（A/2→AcosC/2）。此时cosC为1以下的值。也就是说，当相位偏移时，转矩提升量将减少。

相转矩：τ=A•磁力(=电流)•sin(θ)
τ=A•sin(θ(θ–C))•sin(θ)
τ=A•(−12(cos(θ–C+θ)–cos(θ–C–θ)))
τ=−A2(cos(2θ–C)+A•cos(C)/2)
τ=sin(2θ)+D

用图来表示的话，则是下图所示的波形。如果角度偏差30度，则上述公式中的D相对于上次的B将是cos 30°，是0.866倍。因此，总转矩也减少了0.866倍。

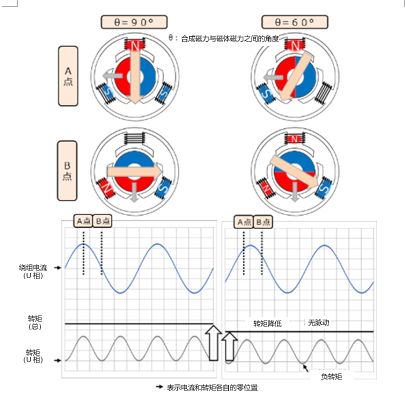
这也可以通过由合成磁力计算总转矩来证实。假设电流向滞后方向偏移30度，那么上述公式中的θ将为60度。θ为90度时sin90°=1，相应地，sin60°为0.866倍。

对图中θ为90度和60度时的两个总转矩进行比较，可以看出虽然电流大小几乎没变，但60度时的输出转矩较小。换句话说，可以说电机的效率变差了。另外，I-T特性乃至S-T特性也会受到这种电流相位变化的影响。

所以，对于总转矩变化的原因，从不同的角度有不同的表达方式。例如，可以说“由于合成磁力与磁体磁力的角度差θ不是90度，所以sinθ小于1”。也可以表述为“因为相转矩中出现了负值部分”。

正弦电流的时序偏差会导致效率发生变化，这是电机性能中的一个重要现象，但另一个需要注意的要点是，转矩脉动可能不会改变。

接下来，我们来了解一下，在具有正弦波状电流的正弦波驱动中，电流的相位与要施加的正弦电压本质上有所不同。这对于正弦波驱动而言是非常重要的要点。

无刷电机：正弦电流的相位变化

关于正弦波驱动中正弦电流的相位，如果所施加电压的相位直接成为电流相位，那么控制会相对简单。然而，受各种因素的影响，实际上电流相位相对于所施加电压的相位会发生变化。前面也提到过，电压和电流可以用下列公式表示：

V–Vbemf=R•I+LdIdt

从这个公式可以看出，电流的相位受电感和感应电压的影响。这使得电机电流的控制难度增加。

以下是相位变化的一些示例：
＜电感分量引起的相位延迟＞
由于绕组具有电感特性，因此正弦电流相对于差分电压（施加电压-感应电压）会向滞后方向变化。该延迟的相位量会受电压的频率（即电机的转速）影响而变化，无法控制为恒定值，因此是个难点。这种延迟会导致电机效率下降。

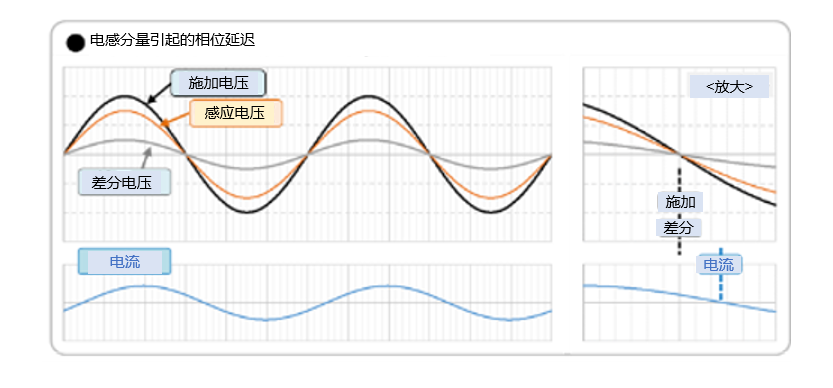
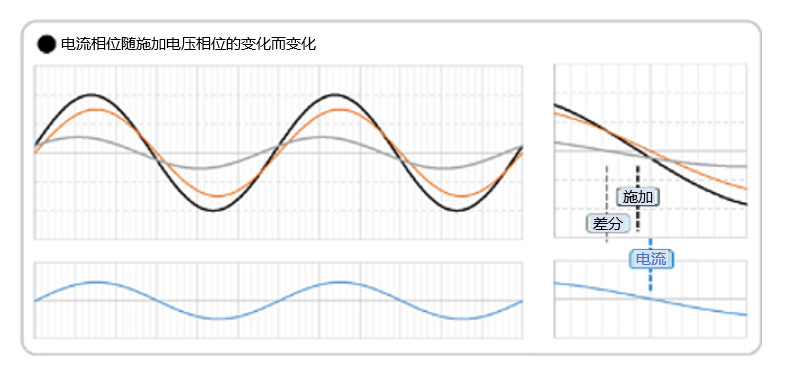
＜电流相位随施加电压相位的变化而变化＞
施加电压的相位是相对于感应电压的相位差。当施加电压相位超前时（下图左侧），差分电压也会超前，所以电流相位会超前。利用该特性，可以使受上述电感分量影响而延迟的电流相位恢复，从而避免电机效率下降。在电机驱动器中，这种使施加电压相位超前的操作称为“超前角控制”。

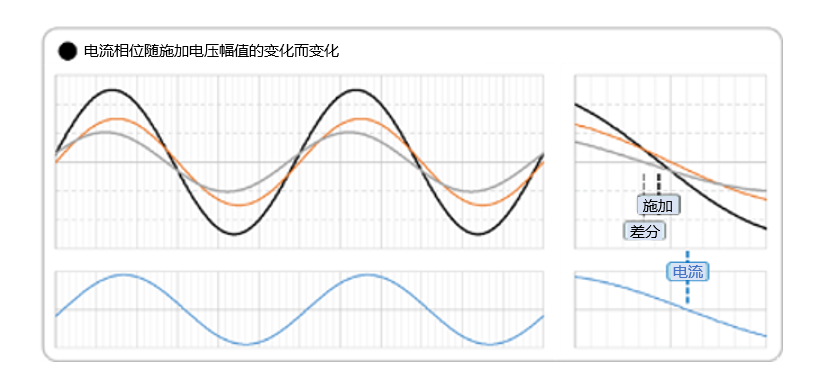
＜电流相位随施加电压幅值的变化而变化＞
通过上述超前角控制，可以使电流相位超前，但被称为“超前角量（超前角值）”的相位调整量，要想保持电机效率的最佳状态，不能是恒定值。这是因为不仅电流相位的延迟量随频率变化而变化，而且例如当施加电压的幅值变化时，差分电压的相位也会变化，并导致电流相位变化。当感应电压的大小发生变化时，也是一样的道理。

电流相位对电机的转矩和效率影响非常大，从上述调整控制的复杂性来看，也可以看出电流相位是一个非常重要的特性。（*这省略对电枢反应相关内容的介绍）

无刷电机的超前角控制（超前角调整）

再重复一个知识点：电机驱动器是通过检测转子的位置并根据检测结果施加相应的电压来使电机旋转的。另外，关于施加电压的时间点，最终必须考虑绕组电流产生的绕组磁场（电磁体磁场）的大小和方向。这种时间点的调整方法之一就是“超前角控制”。

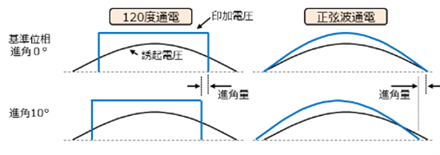
在介绍超前角的概念之前，我们先来了解一下电压施加时间点的标准。如果是正弦波驱动，标准时间点是与感应电压相位相同的位置。如果是120度驱动，则标准时间点位于感应电压的中心与120度驱动波形的中心一致的位置。

超前角控制是指使施加电压的相位相对于该基准相位（位置）超前并输出的控制。因此，以零超前角的位置为基准相位，从那里超前的量称为“超前角量（超前角值）”。这种超前角控制不仅可以适用于正弦波驱动，还适用于120度驱动。

下图为调整超前角时的电机转矩变化示例。图的上半部分是120度驱动时超前角0度与超前角15度的比较；下半部分是正弦波驱动时超前角0度与超前角13度的比较。

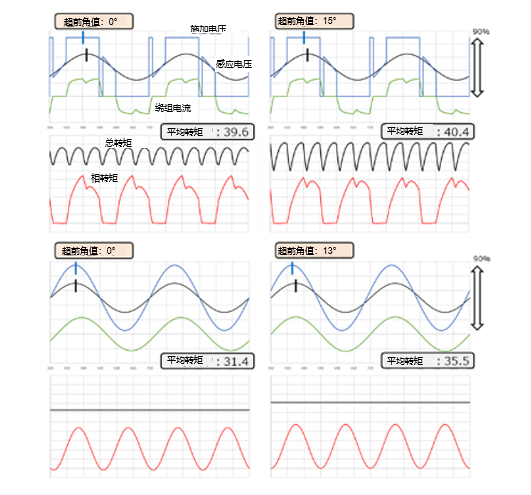
首先可以看出，在正弦波驱动中，13度超前角时的平均转矩比0度超前角时要高。这是因为当超前角为0度时，电流趋于滞后，通过超前角调整后又恢复了。

另外，在120度驱动中，通过超前角调整，总转矩上升。但是问题在于脉动也同时变大。

另外，该数据还体现出以下两点：

1. 与正弦波时相比，120度驱动时因超前角调整带来的转矩变化较小。换言之，可以说120度驱动时不易受电流相位偏移的影响（效率恶化较少）。这可以认为是由于120度驱动时在绕组中有未流过电流的部分。
2. 虽然是与超前角控制没有直接关系的内容，不过在这里还是稍微讲一下：尽管施加了同等幅值的电压，正弦波中表示转矩的数值还是较低（在上图示例中，120度驱动：40左右。正弦波驱动：30出头）。这是因为120度驱动时与正弦波驱动时相比，施加在绕组间的电压（线间电压）最大值不同。

无刷电机：正弦波驱动的各种波形

绕组间施加的电压大小是电机控制中的关键点之一。电机需要以预期的转速和转矩旋转，因此电机的磁体磁力和绕组规格等设计旨在产生所需的输出（转速和转矩）。因此，需要尽可能地避免前述的因驱动波形（在这里是120度驱动和正弦波驱动）的不同而造成的输出范围变化，这一点非常重要。在这里，将为大家介绍最大输出变化的原因以及输出上升的几个正弦波驱动波形。

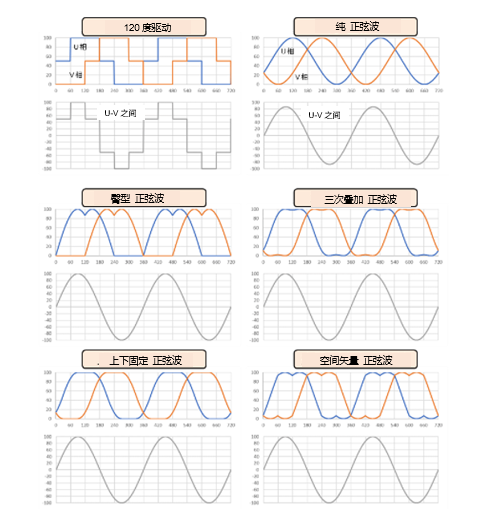
首先，我们来看一下目前一直在探讨的正弦波驱动的波形（下图第一行右侧）。这种方式是在电源电压范围内（图中为0～100）直接创建正弦波形状，在这里我们称之为“纯正弦波”。如图所示，这种形状的话，最大的是下限为0、上限为100的正弦波，乍一看好像与120度驱动时一样（120度驱动也是下限为0，上限为100）。

现在我们来看一下决定绕组电流的电压。绕组电流取决于各相的电位差，因此，是线间电压决定电流的大小，也就是电机的输出。

通过对纯正弦波和120度驱动时的线间电压进行比较，可以看出电压宽度是有所不同的。120度驱动是从-100到100，宽度为200；而纯正弦波则是从-86.6到86.6，宽度为173.2。因此，可以说与120度驱动相比，纯正弦波驱动时的输出范围较窄，电压利用率较低。这就前述的正弦波驱动转矩低的原因。

正弦波驱动比120度驱动更安静，但其缺点是电压利用率较低。出于这个原因，目前已经设计出很多电压利用率更高的正弦波驱动波形。上图中的第2行和第3行这4个波形是主要波形。其中相电压看起来不像“正弦波”的波形较多，但线间电压都是没有失真的正弦波。这4个波形的最大线间电压都与120度驱动时相同。

在电机驱动器中，图中“臀型正弦波”波形应用广泛。这种正弦波也叫“双相调制正弦波”、“底部固定方式”等。用示波器观察波形时，还需要同时确认驱动波形的变化情况。

至此，我们已经了解了使用电机驱动器驱动无刷电机时可以看到的现象和电路行为。还了解了示波器波形、感应电压、电机转速调整工作、电源电流、输出特性、转矩脉动、电流波形等内容，这些都是在驱动电机时需要了解的基础知识。

使用电机时，毋庸置疑需要获得预期的输出特性（转速、转矩），而这就对效率、静音和可靠性提出了要求。电机驱动器的开发人员也是为了实现这些要求和目标而进行开发和改进研究的。这里介绍的内容是实现目标所需要最低限度的基础知识，因此请务必扎扎实实地了解清楚。