交流电路是电子工学的基本概念之一，是指电流和电压随时间变化的电路。这种变化通常具有类似正弦波的周期性波形。交流电路主要由电阻器、电容器、电感器和晶体管等电子元器件组成。在实际应用中，通过这些元器件的不同组合，可以设计出具有各种功能的电路。要想驾驭交流电路，就需要掌握波形和特性分析、计算以及设计技能，以便能够预测电路行为、锁定问题点并实现最佳设计。

本文将介绍交流电路的工作原理和基本要素等基础知识。

交流电路基础知识

交流电源和波形

交流电路的起点是交流电源。交流电源通常为正弦波形。正弦波会随时间的变化而呈周期性变化，其周期和幅度是很重要的参数。通过波形周期性变化，可实现供电和信号传输。

周期

周期是交流波形形成一个完整周期所需的时间。周期通常用“T”表示，单位为秒（s）。例如，正弦波形形成一个周期所需的时间就是一个周期。

频率

频率是表示单位时间内波形振荡次数的指标。频率通常用“f”表示，单位为赫兹（Hz）。

振幅

振幅表示波形峰值（最大值或最小值）的大小。振幅通常用“A”表示，表示电压或电流的最大值，即波形的强度或能量大小。

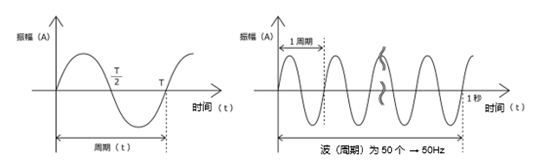
频率是波形周期的倒数，表示每秒的周期数。频率以用“Hz（赫兹）”表示，频率高的波形周期短。例如，50Hz的交流电源每秒周期性变化50次。

交流电路是电流和电压随时间变化的电路。其典型特性之一是“交流波形”。交流波形通常具有类似正弦波的周期性波形。

交流波形有多种类型，每种类型都有不同的特性。

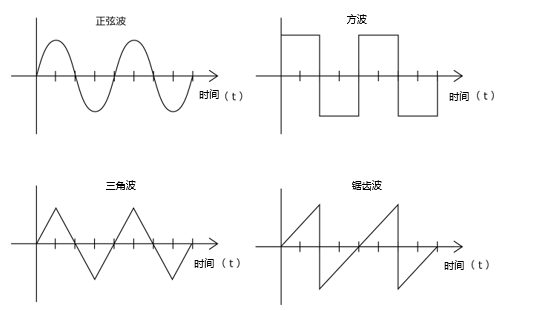
常见的周期波形

正弦波：连续且平滑的波形。这种波形是周期性的，重要参数包括振幅、频率和相位角。
方波：电压主要在高电压和低电压两个不同的电平之间交替、且变化急剧的波形。
三角波：其形状与正弦波相似，但增减更急剧。三角波的角频率比正弦波更高。
锯齿波：一种连续上升的波形，主要是线性增加的坡度，表示急剧的变化。

平均值和有效值（RMS值）

在交流电路中，波形的平均值和有效值是基本指标。平均值是波形的时间平均值，是整个波形的面积除以时间得到的值。而有效值与波形的振幅有关，表示与平均值具有相同功率效应的直流电压值。

相位差

在交流电路中，多个波形之间可能会产生相位差。相位差表示波形周期内的时间偏移，相位差会影响到波形的形态等一些特性。另外，波形延迟表示电路内产生的时间延迟，在信号处理和控制系统中该参数尤为重要，在波形合成和电路设计中都是必不可缺的要素。

复数

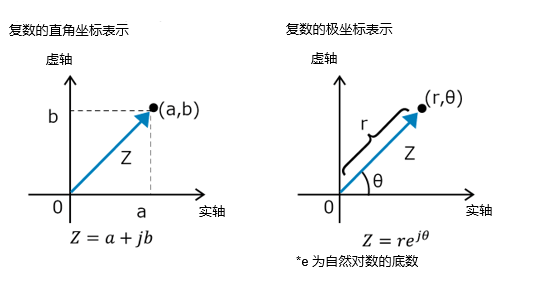
复数表示和极坐标系是交流电路分析中非常有用的数学工具。复数表示由实部和虚部组成，可以简洁地表示波形振幅和相位信息。极坐标系提供了一种将复数表示转换为极坐标形式的方法，有助于直观地了解波形的振幅和相位。

阻抗

在交流电路中，“阻抗”是相当于“电阻”的概念，不仅需要与电阻结合在一起考虑，还需要与线圈和电容器等一起考虑。阻抗以复数表示，其大小和相位可以表征波形的性质。

串联电路与并联电路

在串联电路中，元器件串联连接。要计算串联电路的特性，需要使用欧姆定律或相量符号来求合成阻抗和电流。

在并联电路中，元器件并联连接。要计算并联电路的特性，需要使用倒数定理或相量符号来求合成阻抗和电流。

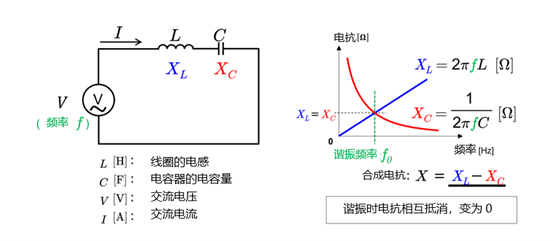
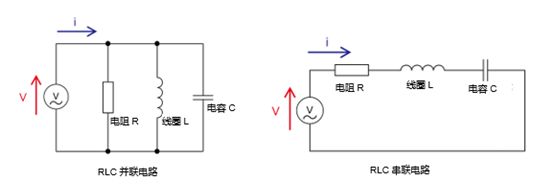
如下图所示，连接电阻器（R）、线圈（L）、电容器（C）的电路分别称为“RLC串联电路”和“RLC并联电路”，它们的共同特点是阻抗随频率的变化而变化。在串联电路中，阻抗会受到各元素的综合影响；而在并联电路中，各元素的阻抗同时存在并产生影响。

交流电路的波形和特性

在交流波形中，频率和周期时间是基本特性。频率表示单位时间内波形重复的次数，周期时间表示一个周期所需的时间。

频率

频率是表示波形在单位时间内重复次数的指标。通常，频率用“赫兹（Hz）”表示，1赫兹表示每秒一个周期。可以使用以下公式计算频率（f）：

\(\text{频率(f)} = \frac{1}{\text{周期 (T)}}\)

其中，f是频率，T是周期时间。频率表示波形的振荡速度或重复率，较高的频率表示周期时间较短，较低的频率表示周期时间较长。

周期时间

周期时间表示波形完成一个周期所需的时间。周期时间通常用“秒（s）”来表示。周期时间（T）和频率（f）之间的关系式如下：

\(\text{周期（T）} = \frac{1}{\text{频率（f）}}\)

周期时间定义了波形的周期性；周期时间越短，波形振荡速度越快，周期时间越长，波形振荡速度越慢。

平均值

平均值是表示波形振幅平均值的指标。平均值通常用“Ave”或“μ”表示，通过下面的公式计算：

\(V_{\text{Ave}} = \frac{V_1 + V_2 + V_3 + \ldots + V_N}{N} = \frac{1}{T} \int_0^T V(t) \, dt\)

其中，Ave是平均值，T是周期时间，x(t)是时间t中的波形值。

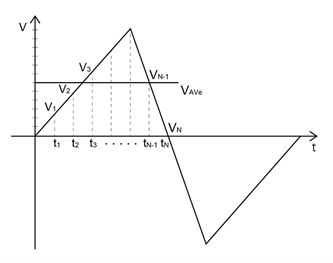
平均值表示整个波形的振幅平均值，计算时需要考虑到波形的正负区域。平均值表示波形的中心，当波形对称时，平均值为零。在纯正弦波的情况下，该平均值等于0.637×Vmax。这种关系也适用于电流的平均值。

平均值在下面列出的电源供给、信号处理和电流控制等应用中很重要：

电源供给：当供给交流电时，功率的平均值是电源效率的指标
信号处理：直流分量电平的降噪等
电流控制：电机驱动、控制系统等中的电流控制

交流电路的计算

复数的基础知识和应用

复数由实部和虚部组成，通常表示为“a+bj”。其中a是实部，b是虚部。复数j是虚数单位，具有“ｊ²=-1”的性质。

复数也可以通过极坐标形式来表示。在极坐标形式中，复数由振幅和相位角表示。极坐标形式以如下公式表示：

\(z = A \cdot e^{j\theta}\)

其中，A表示幅值，θ表示相位角，j表示虚数单位。

在交流电路中，阻抗是确定电流和电压关系的关键要素。阻抗的计算涉及到电阻、电感和电容的组合，可以认为阻抗是用来确定交流电路中电流和电压关系的复杂电阻。

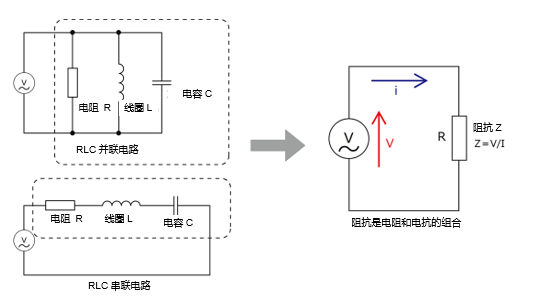
阻抗的计算

阻抗通常用复数表示，由实部（电阻）和虚部（电抗）组成，公式如下：

\(Z = R + jX\)

其中，Z是阻抗，R是实部（电阻），X是虚部（电抗），j是虚数单位。

电阻

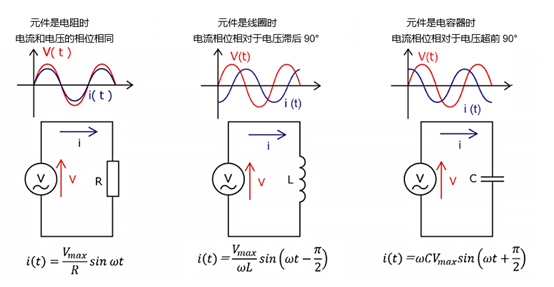
电阻是直接控制电流和电压关系的元件。电阻值（R）用电压（V）和电流（I）之比来表示，适用欧姆定律。

\(V = I \times R\)

电阻会影响功率损耗和信号的衰减，表示交流电路中的能量损耗。

电阻的阻抗是电阻本身，取决于电阻值。阻抗与电阻的单位相同。

\(Z_R = R\)

电感

电感取决于线圈和绕组的形状，是导致交流电路中电流延迟的因素。电感值表示电流变化时会感应到电压。因此，电流急剧变化时电压上升，电流缓慢变化时电压下降。

线圈的阻抗由线圈的电感值（L）和角频率（ω）表示，公式如下：

\(Z_L = j\omega L\)

其中j是虚数单位。

电容（Capacitance）

电容（Capacitance）也称为“电容器（Condenser）”，具有存储电荷的能力。电容值（C）表示电压变化时存储的电荷量。当电压急剧变化时释放电荷，当电压缓慢变化时提供电荷。

电容器既可用于直流电路，也可用于交流电路。在直流电路中，电容器负责存储电荷并提供能量，在电路的稳定性和信号整流方面发挥着重要作用。而在交流电路中，电容表示取决于频率的电抗，在改变信号相位差方面发挥着重要作用。

其基本结构是在两个导体（通常是金属板）之间夹着电介质（绝缘体）。电介质积蓄电荷，积蓄的电荷被作为电场能存储起来。电容器的电容量（电容值，C）表示可以存储的电荷量，用“法拉（F）”表示。

电容器的阻抗由电容器的电容量（C）和角频率（ω）表示，公式如下：

\(Z_C = \frac{1}{j\omega C}\)

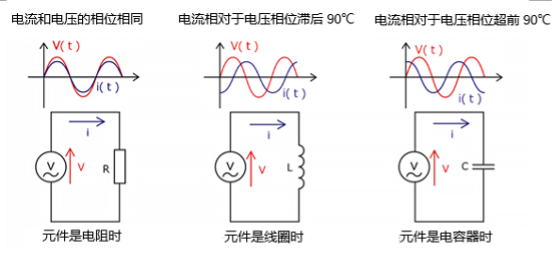
在交流电路分析中，相位差和电抗是很重要的概念。相位差表示波形的时间偏移量，电抗表示线圈、电容器等组件的阻抗。

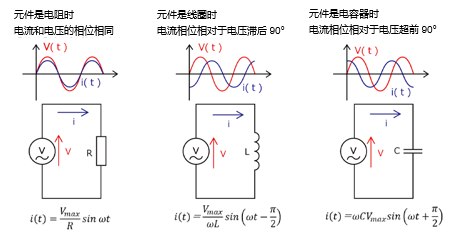
相位差产生的原因及其影响

相位差是因为线圈（Inductor）和电容器（Capacitor）对交流信号的响应不同，并具有取决于频率的电抗而产生的。

这种相位差对电路工作具有以下的影响，因此在交流电路的设计和分析过程中，管理和调整相位差是很重要的工作。

功率传输和损耗：

如果没有相位差（相位为零），电流和电压将同时达到峰值。这可以最大程度地传输功率并最大程度地减少损耗。而当产生相位差时，电流和电压的峰值会有偏移，这可能会降低功率传输效率。当存在相位差时，电流和电压波形会发生偏移，从而会产生不必要的能量损失——无功功率（Reactive Power）。

电路稳定性：

当产生相位差时，就会发生谐振，即在特定频率处振动最大的现象。当谐振与相位差结合时，电路的响应就会发生变化。另外，电路的特性在不同频段可能会有波动。

在反馈电路等相位是重要因素的电路中，相位差的变化有助于电路的稳定性。

相位差的计算

相位差表示在交流电路中电流和电压的波形随时间偏移的程度。通过弧度来计算相位差是广为使用的方法。

1. 角频率的计算：
   通常使用频率f来求角频率ω。
   \(\omega = 2\pi f\)
2. 相位差的计算：
   相位差 ϕ 是通过时间t和角频率ω的乘积求得的。
   \(\phi = \omega t\)
   例如，当频率f=50Hz时，对应的角频率ω＝2π×50。
   如果t=0.01秒，则相位差ϕ＝(2π×50)×0.01。

电抗的计算

电抗是表示线圈和电容器等组件的交流阻抗的指标。电抗通常用“X”来表示。电容器的电抗取决于角频率ω。电容器具有存储电场能和积蓄电荷的特性。当交流信号施加给电容器时，先是电流流动，积蓄电荷；然后电流反向流动，释放电荷。电流的这种延迟是由电容器的电抗造成的，最终会产生电流相对于电压超前的现象。这种超前被视为相位差。

电容器的电抗按下面的公式计算：

\(X_C = \frac{1}{2\pi fc}\)

其中，X_C是电容器的电抗，f是频率，C是电容器的电容量。

线圈的电抗也与角频率ω成正比。因此，当频率变化时，线圈的电抗也会发生变化。当交流信号施加给线圈时，线圈内会产生磁场，从而影响线圈的电感值。该磁场的产生和崩溃需要时间，最终会导致电流相对于电压滞后的现象。这种滞后也被视为相位差。

同样，线圈的电抗计算公式如下：

\(X_L = 2\pi fL\)

其中，X_L表示线圈的电抗，f表示频率，L表示线圈的电感。

在交流电路中的应用

线圈的电抗X_L=jωL和电容器的电抗会因角频率而产生相位差。当这些元器件安装到电路中后，相位差会影响到整个电路。

例如，在RC电路（电阻器和电容器的组合电路）中，会因电容器的电抗和电阻的影响而产生相位差。当改变频率时，相位差会随电抗的改变而变化。利用这一特性，可通过频率来控制RC电路的特性。

交流电路的实际使用和设计

1. 1. 明确目标
   电路设计的第一步是要明确设计目标。需要确认需要实现哪些功能以及有哪些限制条件。
2. 2. 选择组件
   设定目标后，需要选择适当的组件。电阻器、电容器、线圈、晶体管和二极管等元器件的选择对于设计能否成功具有很大的影响。
3. 3. 创建电路图
   使用选定的组件创建电路图。需要考虑组件的布置和连接，以确保它们在电路图上得到准确表示。
4. 4. 计算阻抗
   计算组件的阻抗并了解电路的响应情况。使用综合阻抗来评估整个电路的特性。
5. 5. 制作原型
   设计进行到一定阶段后，就可以制作实际的电路原型了。需要使用原型来验证设计妥当与否，并根据验证结果进行调整。

选择合适的电源是提高电路性能、可靠性和效率以及实现设计目标的关键。所以需要好好规划并选择符合规格要求的电源。

1. 电压和电流条件
   明确电路正常工作所需的电压和电流必要条件。这些条件规格对于确保电路稳定运行并实现设计目标而言至关重要。电压条件是指电源提供的电压情况，而电流条件是指电路消耗的电流。这些条件规格对电路性能和特性有着很大的影响。
2. 稳定性和可靠性
   所选的电源需要确保电路的稳定性，并确保运行的可靠性。所以需要考虑电源在电压和电流波动时的稳定性，以及是否需要能够保护电路免受过电压和过电流影响的机制。可靠性高的电源有助于延长使用寿命并提高安全性。
3. 效率和功耗
   高效率的电源有助于节能，可以更大程度地减少功耗。尤其是在电池供电的设备和看重能效的应用中，电源效率是非常重要的。高效率的电源可减少发热量，并降低能源成本。
4. 电源噪声和纹波
   电源的噪声和纹波可能会对电路的正常工作产生不利影响。选择电源时，需要考虑尽可能抑制电源的噪声和纹波。稳定的电源有助于提高信号质量并避免噪声引起的问题。
5. 保护功能
   需要确保所选的电源具有保护电路的功能。过电压保护、过电流保护、短路保护等保护功能，可以提高电路的安全性，确保设备的耐久性。
6. 供应链和成本
   还需要考虑电源的成本和是否容易购买。比如确认特定电源是否可以长期供货，成本是否符合预算。另外还应考虑供应链的可靠性。

电路图是电子工程学和电气工程学领域不可或缺的交流工具，可以一目了然地体现出各种组件和连接情况，有助于理解电子电路的结构和工作。

电路图的要素

组件符号

在电路图中，用符号来表示各种电子组件（元器件）。常见的组件符号包括电阻器、电容器、线圈、晶体管、二极管等。每种组件都有相应的符号来表示其功能。

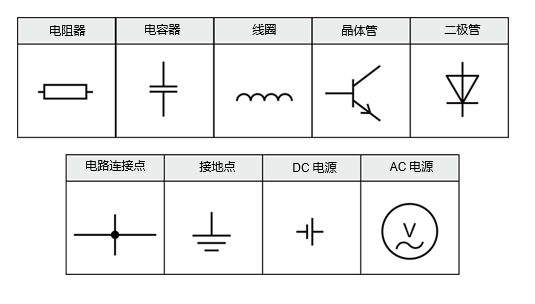
连接线

连接线表示组件之间的电气连接。连接线通常被绘制为直线或曲线，用来连接组件符号和连接点。连接线相交时，可以用点来表示。

电源

电源表示为电子电路提供电力的要素。电源通常用电压源或电流源符号表示，表示由电路的哪个部分供电。

电源地

电源和接地是电路图中的重要要素。通常，电源配置在电路的顶部或左侧，接地配置在电路的底部或右侧。这样更容易看清电路中的电流路径。

在交流电路中，LED（Light Emitting Diode，发光二极管）也应用广泛。下面将介绍LED在交流电路中是如何工作的，以及其主要应用示例。

将LED嵌入交流电路

LED通常用直流电源驱动，因此需要通过电路将LED嵌入交流电路中。以下是在交流电路中使用LED的主要方法。

1. 全波整流

全波整流是将交流电转换为直流电的常用方法。使用整流二极管对正半周和负半周进行整流，获得直流电源。该直流电源被供给LED，使其点亮。

桥式整流是全波整流的另一种形式，是使用4个整流二极管对交流电源进行整流。该方法的效率高，稳定性好，被广泛用于LED点亮。

2. 半波整流

半波整流是一种仅对交流电源的半个周期进行整流来使LED点亮的方法。与全波整流相比，这种方法的效率较低，这限制了其在某些应用中的使用。

LED在交流电路中有着广泛的应用，并且因其高效率和耐久性而被用于众多领域。在高效照明、信息显示、通信和控制系统中，LED已成为不可或缺的技术。

补充

前面我们详细探讨了交流电路的基本概念、阻抗、电容器、欧姆定律以及电流和电压的基础知识。掌握这些基础知识可以为进入更高级的计算和电路设计做好准备。

拉普拉斯变换

拉普拉斯变换是一种将时域信号和响应变换为复频域的数学方法。利用这种变换，可将微分方程转换为代数方程，使分析更容易。进行拉普拉斯变换后，可使用逆变换来恢复原始信号和响应。

谐振

谐振是交流电路中在特定频率下振动被放大的现象。谐振频率下的振动使电流和电压达到最大值，这在某些特定应用中可以带来所需的效果。

在谐振电路的设计中，谐振频率的计算和带宽的调整都是非常重要的。我们将聚焦于谐振电路中各元素的选型方法和设计手法，介绍实现所需谐振特性的方法。

在分析和设计复杂的交流电路时，使用拉普拉斯变换和谐振特性等的高级计算技术，有助于实现实际项目并解决问题。通过学习高级计算技术，可以获得交流电路设计和分析相关的更高级的技能，有助于锁定和解决问题并实现富有成效的设计。

在交流电路的设计中，了解功率因数和功耗是非常重要的。功率因数可评估电源的效率，功耗会影响能效和成本。

功率因数的定义

功率因数（Power Factor）表示交流电路中的有功功率（执行实际有用功的功率）与视在功率（从电源到用电设备的电力传输功率）之比。功率因数通常在0到1的范围内表示，功率因数高表示电力利用效率高，功率因数低意味着有额外的功耗。

功率因数的重要性

功率因数是供电系统的重要指标，功率因数低会给电源和电力传输线路增加负荷，造成能量浪费。保持高功率因数可以提高供电效率，降低供电成本。

功率因数的计算方法

功率因数使用有功功率（W）和视在功率（VA）通过下面的公式进行计算。

\(\text{功率因数} = \frac{\text{有功功率 (W)}}{\text{视在功率 (VA)}}\)

实例

例如，如果某设备的有功功率为100W，视在功率为120VA，则功率因数计算如下：

功率因数 (PF) = 0.833

改善功率因数的重要性

改善低功率因数可以提高供电效率并降低成本。下面是改善功率因数的一些方法。

添加串联电容器

可以通过在电路中添加串联电容器来提高功率因数。电容器具有相位滞后作用，可补偿错误的功率因数。

有源功率因数校正装置

将有源功率因数校正装置插入电源和用电设备之间，可以改善功率因数。这类装置可监测功率因数并进行适当的校正。