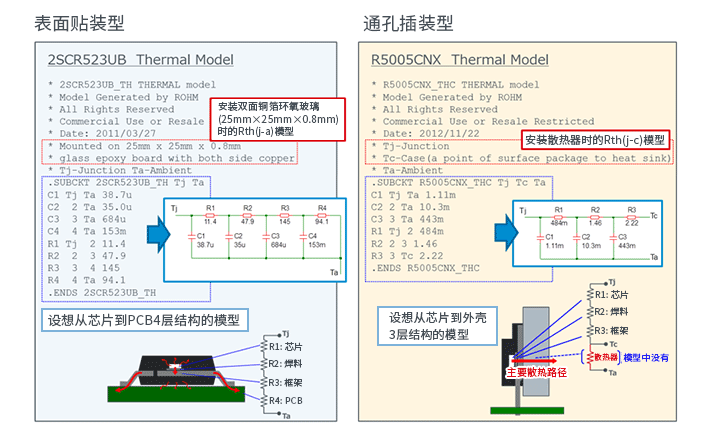
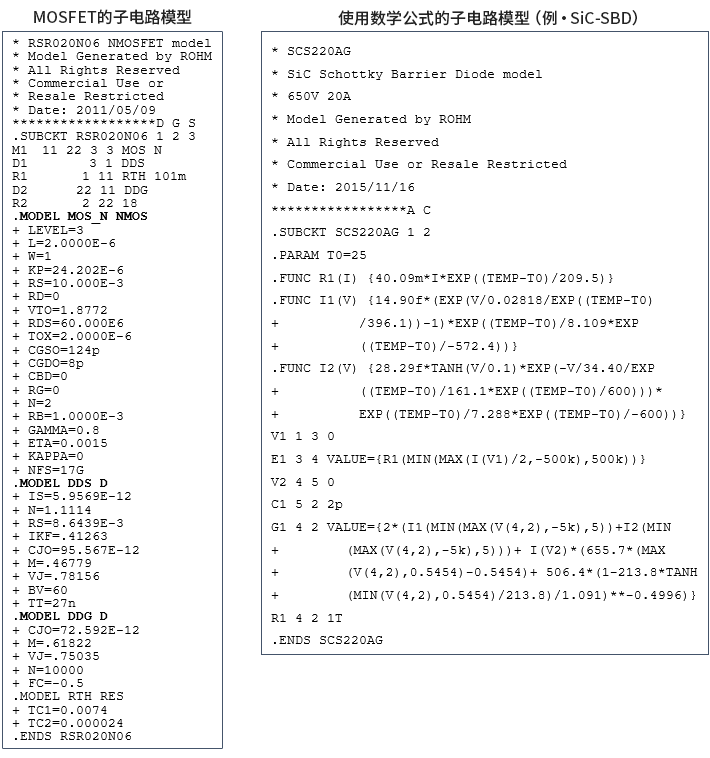
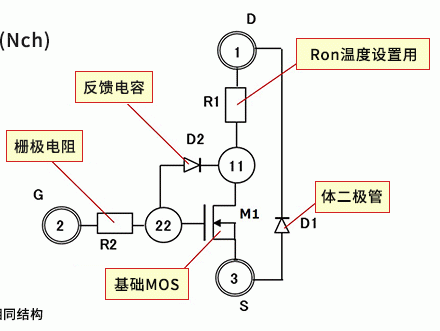
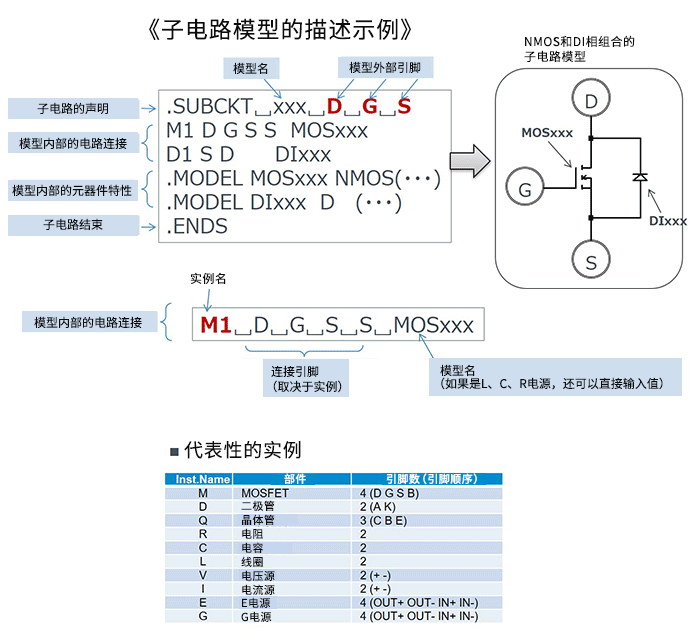
近年来,基于SPICE的模拟器的仿真结果已经非常接近于实际特性。在某些情况下,将其作为一种现实的理想特性,调整实际的电路特性并使之接近这种理想特性,是非常“好用”的工具。然而,某些分析算法、条件设置、器件模型,并非没有收敛性或稳定性方面的课题。更好地了解仿真的收敛性和稳定性课题,有助于更有效地利用仿真这个工具。
SPICE仿真的收敛性与稳定性
所谓仿真中的收敛性问题,是指即使执行了程序也不开始计算、中途停止等问题,导致即使微小的条件变更也能引发结果很大的变化、出现不应该出现的结果等。简而言之,就是分析错误和结果不稳定。
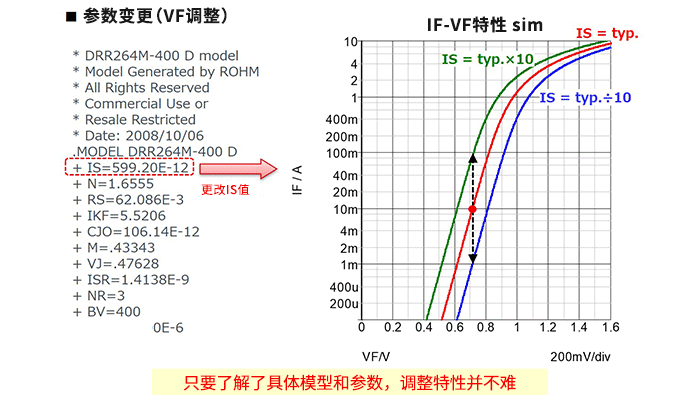
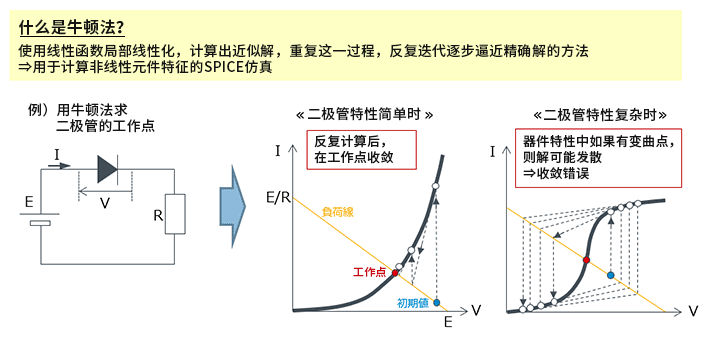
其原因有几种,在这里以“器件模型”这种原因为例来说明。下面是串联连接的电阻和二极管的I-V(电流-电压)特性,与电阻这样的电流和电压简单成正比的线性器件相比,二极管这样的非线性器件的仿真会更复杂。可能任何人都可以轻松地创建电阻I-V特性的计算公式,而二极管正向特性的公式恐怕就没有那么简单了。在下面的示例中,使用SPICE仿真中众所周知的牛顿法,介绍一种通过不断迭代来获得负载线和非线性负载(在这里为二极管)的交点—工作点的近似解的方法。这种器件模型的特性有时是不连续的,在具有变曲点等较复杂的特性情况下,有时会出现如右图所示的“不应该出现的”不收敛的结果。
收敛性和稳定性较差时的处理方法
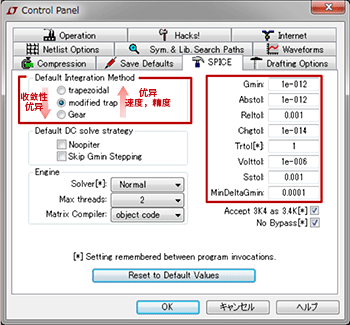
收敛性和稳定性较差时,有几种处理方法。不同的模拟器其处理方法也不同,下面的方法请理解为其中一个示例。模拟器的设置项目中,有收敛性和稳定性相关的项目,试着更改这些项目。在本例中,算法有三个选项,我们将尝试更改现有的选项。另外,也将尝试更改精度和误差等收敛条件。
①尝试将算法更改为Gear
・trapezoidal(梯形法):计算速度和精度高,但收敛性方面表现较差。
・modified trap(梯形法改进版):改善了梯形法的收敛性。
・Gear(预测校正法):容易收敛,但在计算速度和精度方面表现较差。
上述方法是可以在用户处通过更改模拟器的设置等,来规避收敛和稳定性问题时的方法。但其中也有可能是器件模型本身具有缺陷,在这种情况下,是很难在用户处解决仿真错误的。
如果需要创建一个器件模型,最重要的是要创建一个比起精度更重视收敛性和稳定性的、能运行的器件模型。