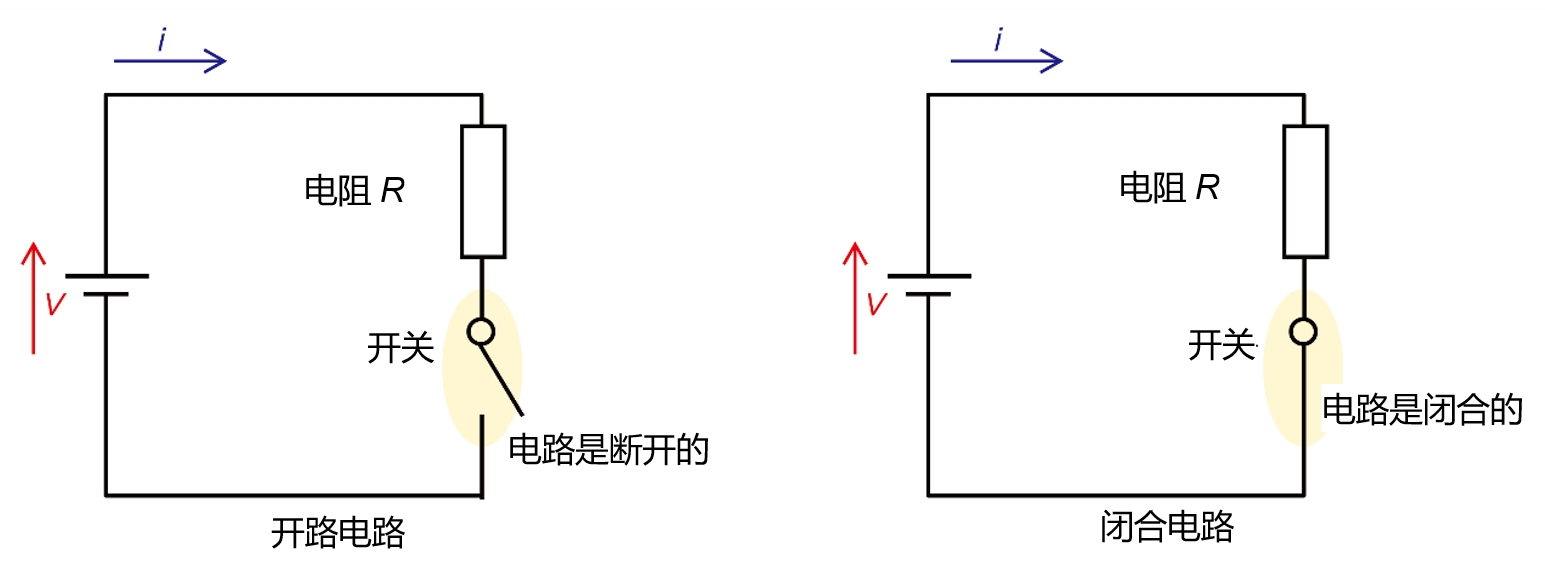
叠加定理(又称“叠加原理”)是一种用于分析包含多个独立电源的线性电路的电路解析方法。运用这一定理,可以分别分析每个电源(无论是DC电源还是AC电源),然后通过代数和将各结果(电压或电流)进行叠加,从而掌握整个电路的工作状态。这种方法的优点是在分析含多个电源的复杂电路时,可以让电路分析更加清晰易懂。例如,在试制阶段的电路板上增加额外电压源,或者遇到多个独立电源并存而需要排查原因的异常工作时,理解叠加定理的使用方法,将会非常方便。本文将从叠加定理的基础知识开始,详细介绍如何分别计算每个电源并最终进行叠加求解的方法及其应用实例。若您希望拓宽电路分析的思路,敬请继续阅读下去。
叠加定理概述
本节将介绍叠加定理所依据的背景和理论基础。在处理包含多个独立电源的电路时,电路是否为线性是一个重要的考量因素。如果具有线性特性,就可以单独考虑每个电源产生的电压和电流响应,然后进行叠加获得最终结果。虽然严格的证明需要从数学角度论证欧姆定律和基尔霍夫定律等线性方程组的叠加特性,但本文将以便于在工程实践中应用的形式进行讲解。
线性电路和叠加定理
线性电路是指输入与输出呈比例关系(线性量),遵循欧姆定律、基尔霍夫电压定律和基尔霍夫电流定律,且不包含非线性元件的电路。典型的线性元件包括电阻器、电容器和电感器等。在仅由这些元件组成的电路中,即使存在多个电压源或电流源,也可以先独立计算每个电源的响应,再进行叠加。
应用叠加定理时,需将多个独立电源逐一“开启”,而将其他电源视为零(电压源短路,电流源开路),并计算在此状态下得到的电压和电流,最后将它们进行代数相加,即可确定整个电路的工作状态。
叠加定理的适用条件
本节将介绍叠加定理的适用条件及应用限制,并结合电路分析中的常见场景,整理线性电路范围内的处理方法。同时,也会探讨与功率计算等相关的注意事项。
适用条件及其理由
只要电路是线性的,就可以应用叠加定理。具体来说,适用条件为输入变为2倍时输出也变为2倍,并且同时施加两个输入时的输出等于分别施加各个输入时的输出之和。这里,我们将尽量避免使用略显抽象的“齐次性”和“可加性”等术语,而是尽可能用通俗易懂的方式进行说明。
- 输入增加,输出也会同比例增加
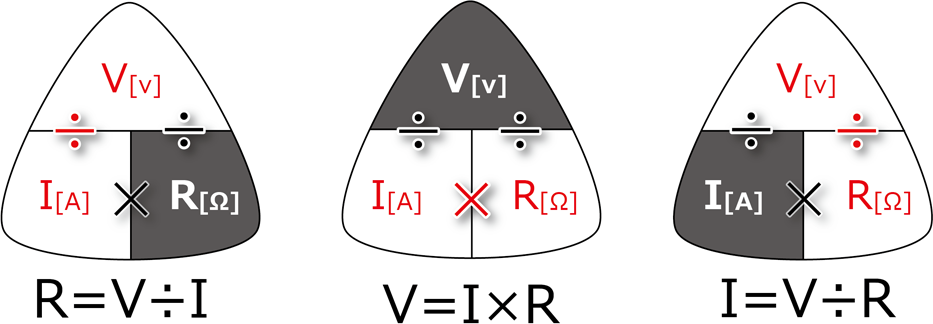
例如,在遵循欧姆定律的电阻电路中,如果将电源电压设为2倍,则由此产生的电流和电阻器上的电压降也会变为2倍。但是,当存在二极管和晶体管等非线性特性时,这种简单的比例关系可能会被破坏。 - 即使同时施加多个输入,其结果也应等于“单独施加每个输入时的结果之和”
例如,当5V电压源和10V电压源接入同一电路时,通过将各自单独施加时的结果相加,是否等于同时施加两个电源时的结果。对于不含二极管等的简单电阻电路,可以认为电阻器的电压降和流过的电流等于每个电源响应的总和。
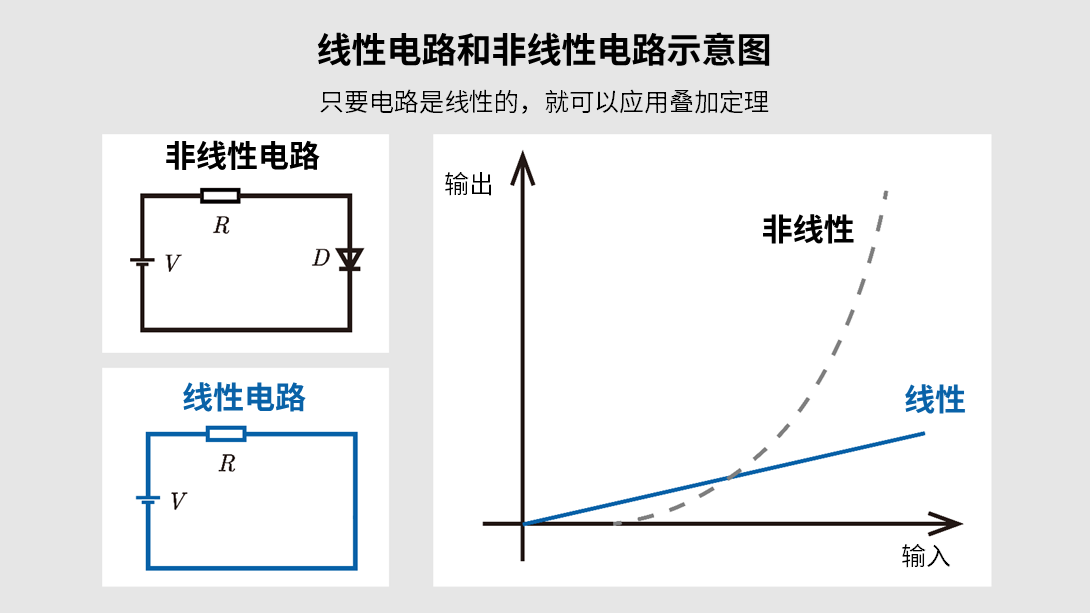
若满足上述条件,则只需单独分析每个电源,再将计算结果相加,就能掌握整个电路的特性。当存在二极管或晶体管的大信号工作区等非线性特性时,可能会出现无法进行简单叠加的情况,但对于纯粹的线性网络,叠加定理是非常有效的。
简单的计算示例
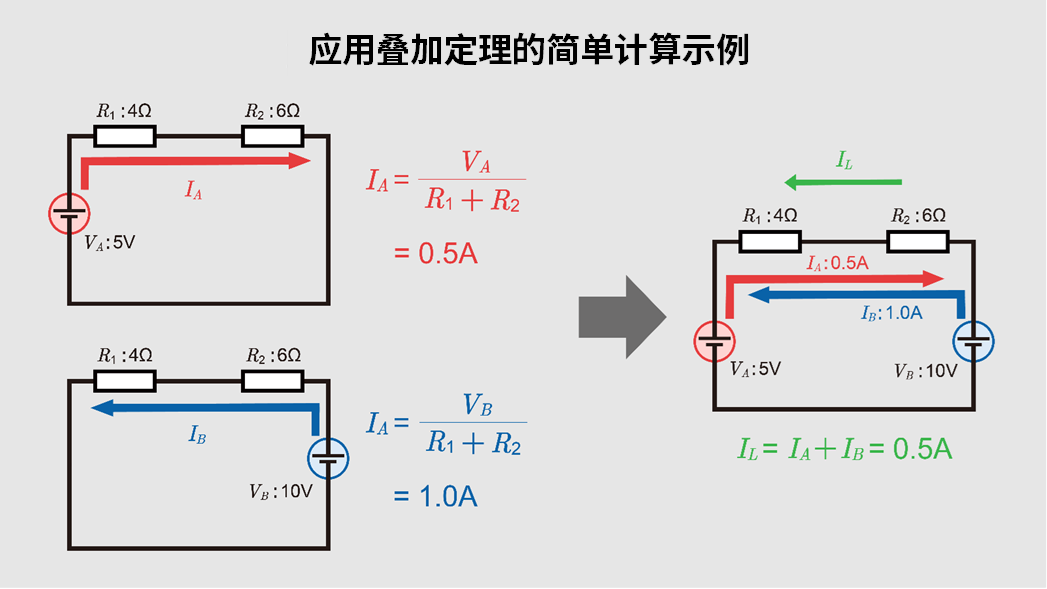
让我们按照先求出串联电阻的总等效电阻,再确认电流和电压降的流程,来体验一下叠加定理。
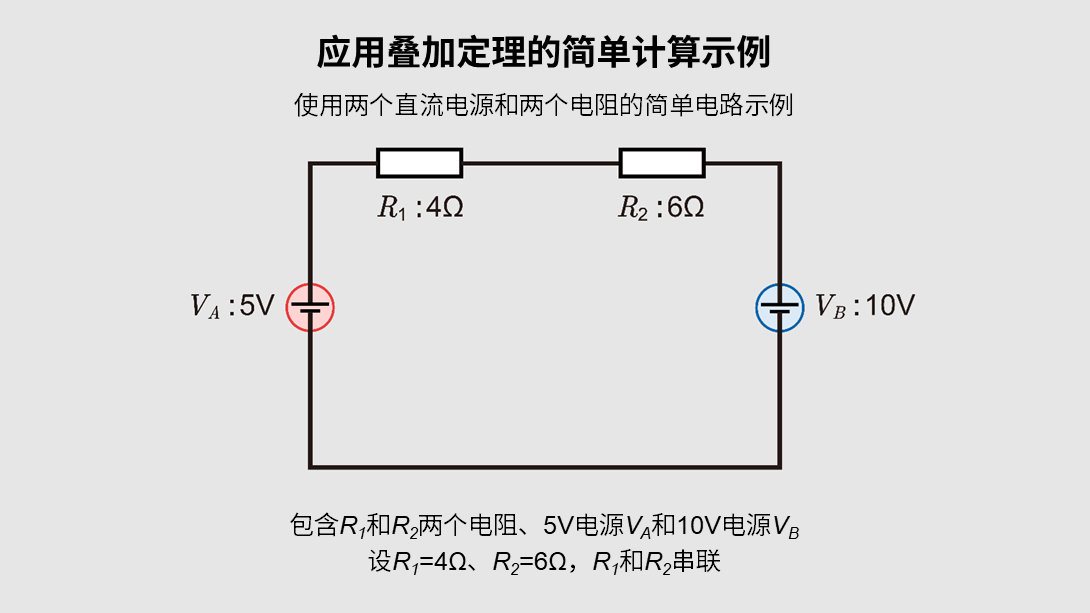
这里我们分析一个具体示例:电阻\(R_1\)和\(R_2\)串联连接,并且存在5V和10V两个直流电源。设\(R_1\)=4Ω、\(R_2\)=6Ω。
- 仅接入5V电源总电阻为4+6=10Ω,所以
\(I_A=\displaystyle \frac{5}{10}=0.5 A\)
\(R_1\)的电压降为0.5A×4Ω=2V,\(R_2\)的电压降为0.5A×6Ω=3V。
- 仅接入10V电源电阻同样为10Ω,所以
\(I_B=\displaystyle \frac{10}{10}=1.0 A\)
\(R_1\)的电压降为1.0A×4Ω=4V,\(R_2\)的电压降为1.0A×6Ω=6V。
- 同时接入两个电源根据叠加定理,每个电阻上的最终电压降等于各个电源单独接入时的电压降数值之和。电流则是方向相反的\(I_A\)0.5A和\(I_B\)1.0A叠加得到的0.5A。实际上需要注意电源是串联还是并联等连接方式,但只要电路是线性的,就可以简单地将各部分的求解结果相加得到最终结果。
叠加定理的基本步骤
接下来将介绍应用叠加定理进行电路分析的具体步骤。为便于初学者理解,我们按步骤进行了梳理。
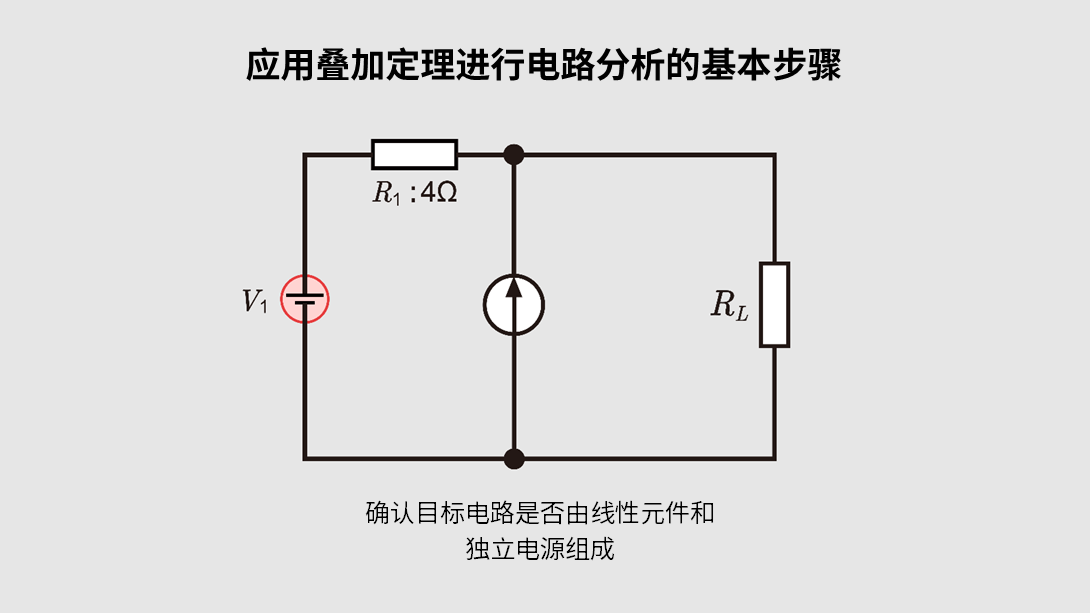
步骤1:确认电路
首先,确认目标电路是否由电阻器、理想电容器和理想电感器等线性元件及独立电源组成,同时检查是否含有受控源或非线性元件(二极管等),以及是否涉及串联、并联、桥式结构或多个网孔等情况。
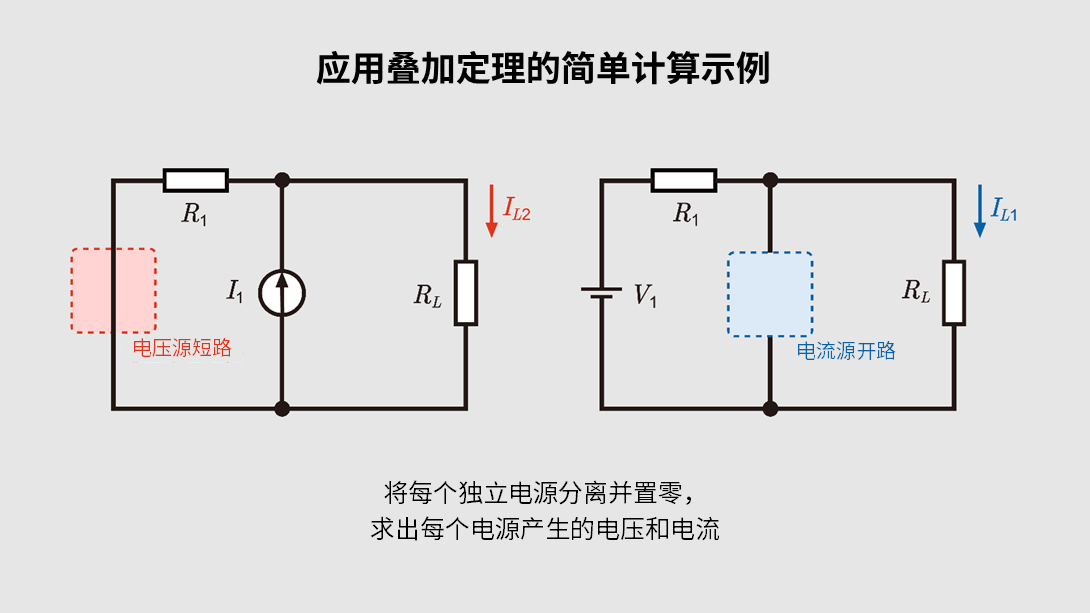
步骤2:仅保留一个电源,其他置零
当电路中含有多个独立电源时,只将其中一个处于“开启”状态,其他均设为关闭。具体操作如下:
- 将电压源置零(视为短路)
- 将电流源置零(视为开路)
以此将每个独立电源分离开来进行分析。通过这种方式,可以区分出每个电源单独对电路产生的影响。
步骤3:计算每个电源产生的电压和电流
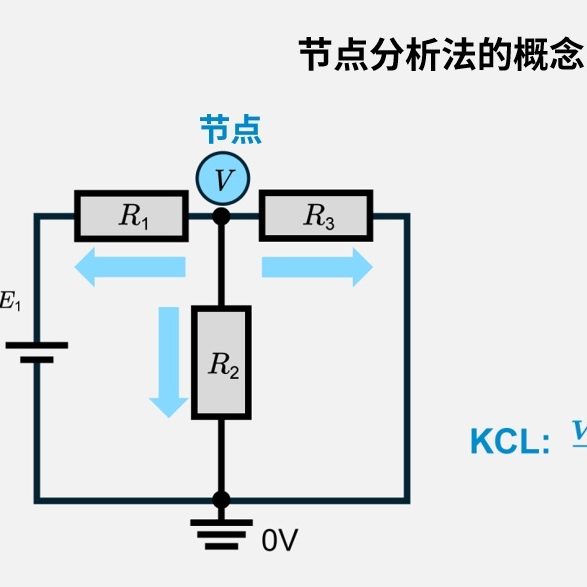
在只保留一个电源的状态下,运用欧姆定律、基尔霍夫定律、网孔分析法或节点分析法等方法,求出各节点的电压和支路的电流,并对所有独立电源重复此步骤。
步骤4:叠加响应得到最终解
最后,将步骤3中得到的各响应以代数和的方式叠加。当出现电流方向相反等情况时,只要在叠加时注意符号,就能求出准确的最终响应。
具体计算示例
例如,当含有独立电源\(V_{S1}\)和\(V_{S2}\)时,首先将\(V_{S2}\)短路(置零),计算仅从\(V_{S1}\)得到的电阻器电压和电流。接着将\(V_{S1}\)短路,仅使\(V_{S2}\)处于激活状态,并进行同样的计算。最后,将每次计算的结果进行叠加(代数和),即可得出各电阻的电压降和流过的电流。
\(I_L=I_{L1}+I_{L2}\)
应用叠加定理的具体示例
本节我们将使用实际数值对电路进行分析,并展示中间计算过程。通过以含多个独立电源的简单电阻电路为例,应该可以更容易理解将各步骤的计算结果进行最终叠加的流程,并且尽量不省略中间的算式,完整地展示出来。
使用两个直流电源和三个电阻的简单电路
电路概要
假设电路中有三个电阻\(R_1\)、\(R_2\)、\(R_3\),一个12V电源\(V_A\)和一个5V电源\(V_B\)。设\(R_1\)=4Ω、\(R_2\)=6Ω、\(R_3\)=12Ω,并假设\(R_1\)串联,\(R_2\)和\(R_3\)并联等连接方式。
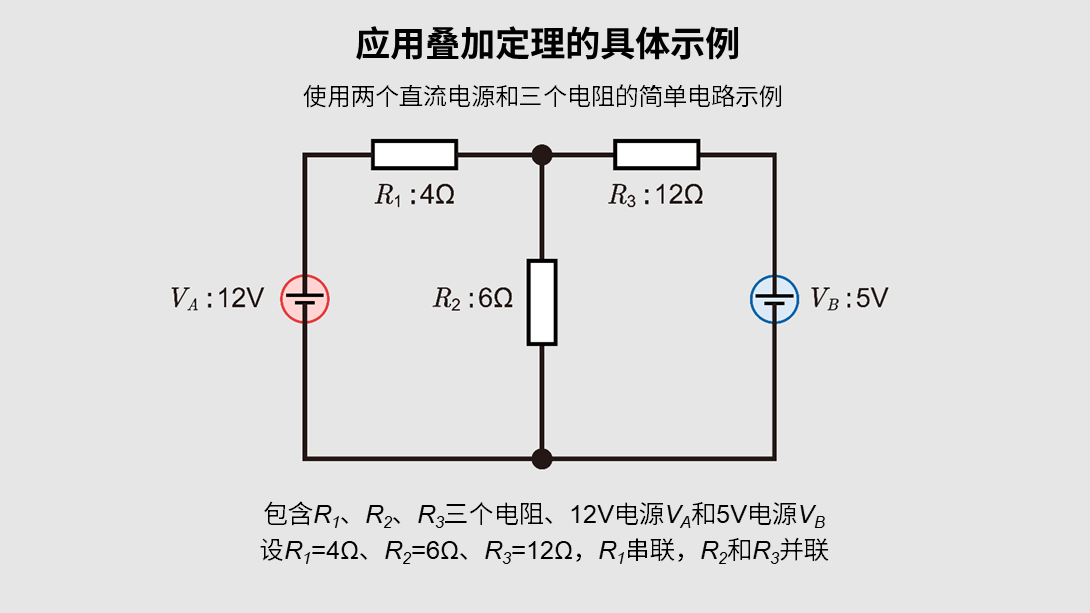
步骤1:确认电路
电路仅由电阻器和独立电源组成,不包含非线性元件,因此可以应用叠加定理。
步骤2:仅激活\(V_A\),将\(V_B\)短路
- 将\(V_B\)短路后,\(V_B\)端子间的电压为0V。
- 由此,电路就变成了由\(V_A\)和三个电阻组成的单电源电路。
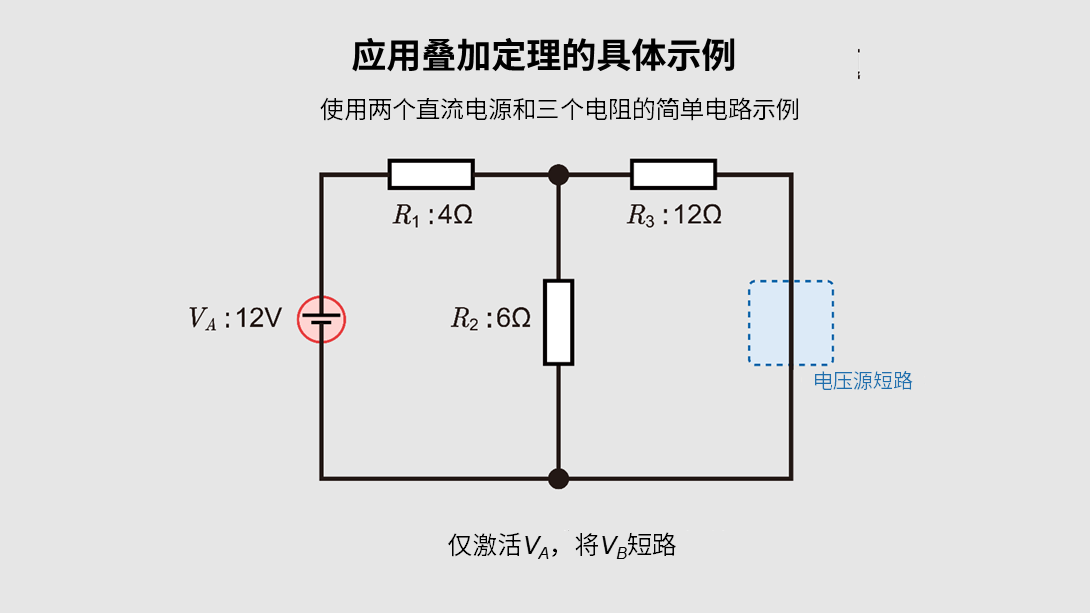
- 运用基尔霍夫定律等方法计算电流及各电阻的电压降。
\(R_{total}^A=R_1+(R_2 || R_3)=R_1+\displaystyle \frac{R_2×R_3}{R_2+R_3}=8\)
\(I_A=\displaystyle \frac{12}{8}=1.5 A\)
按照同样的方法,可以计算出施加在每个电阻上的电压降等。
步骤3:仅激活\(V_B\),将\(V_A\)短路
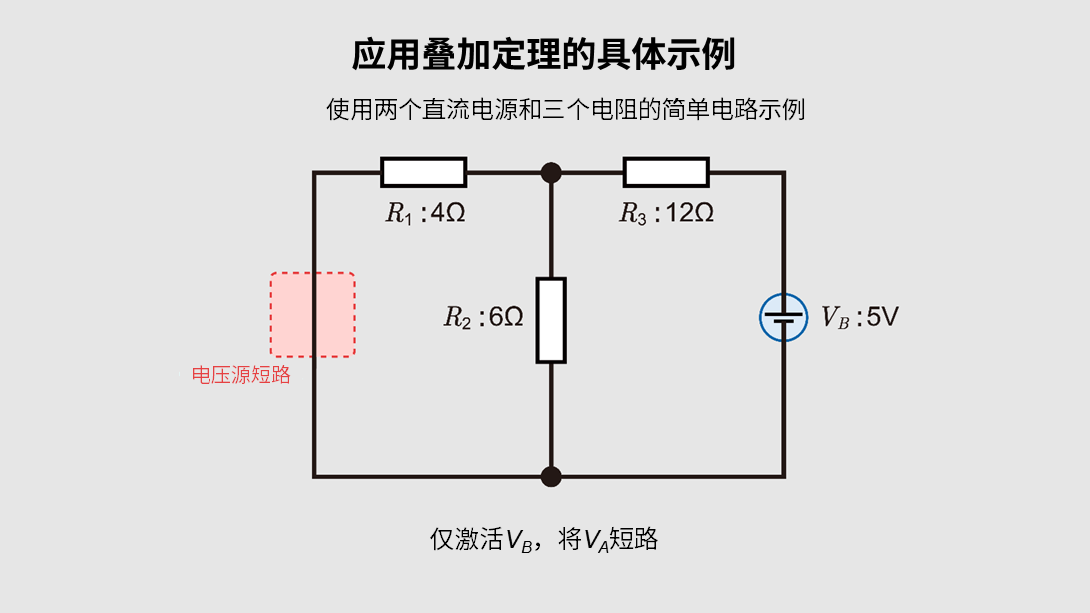
按照同样的步骤,这次将\(V_A\)短路,仅在电路中保留\(V_B\)=5V。总电阻为14.4Ω,所以得出:
\(R_{total}^B=R_3+(R_1 || R_2)=R_3+\displaystyle \frac{R_1×R_2}{R_1+R_2}=14.4\)
\(I_B=\displaystyle \frac{5}{14.4}≈0.347 A\)
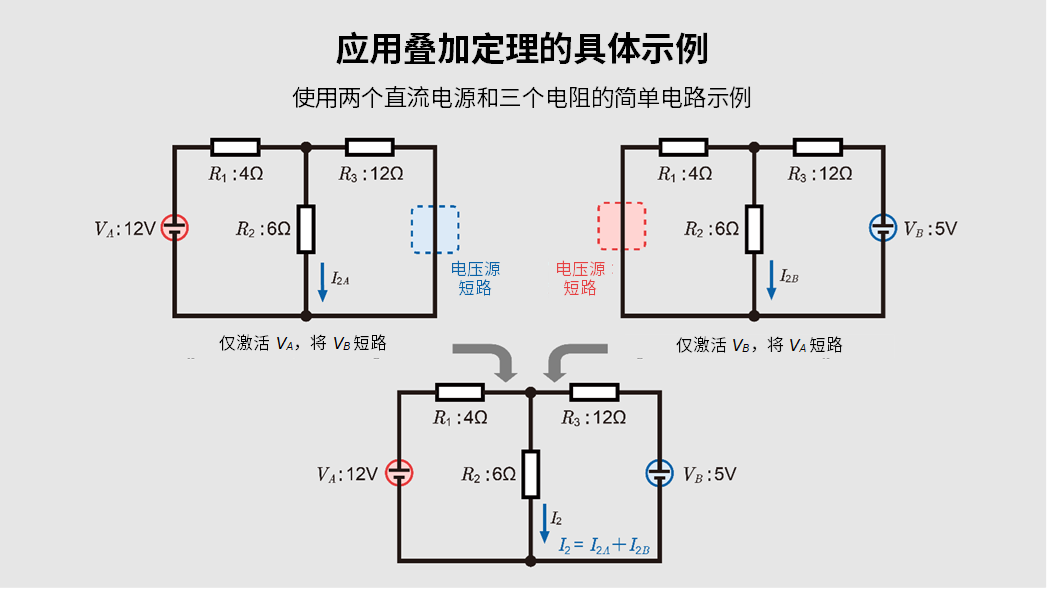
步骤4:对各响应进行叠加
例如,流经\(R_2\)的总电流可以运用分流定律进行计算。\(I_{2A}\)=\(I_A\)(1.5A)×(\(R_3\)/(\(R_2\)+\(R_3\)))=1.0A、\(I_{2B}\)=\(I_B\)(0.347A)×(\(R_1\)/(\(R_1\)+\(R_2\)))≈0.138A,\(I_2\)由\(I_{2A}\)+\(I_{2B}\)计算得出,即\(I_2\)=1.0A+0.138A=1.138A,通过同样的方法,即可求出流经各电阻和各支路的最终电流和电压。
叠加定理与其他分析方法的联合运用
本节我们将介绍叠加定理如何与网孔分析法、节点分析法和戴维南定理等其他方法结合使用。
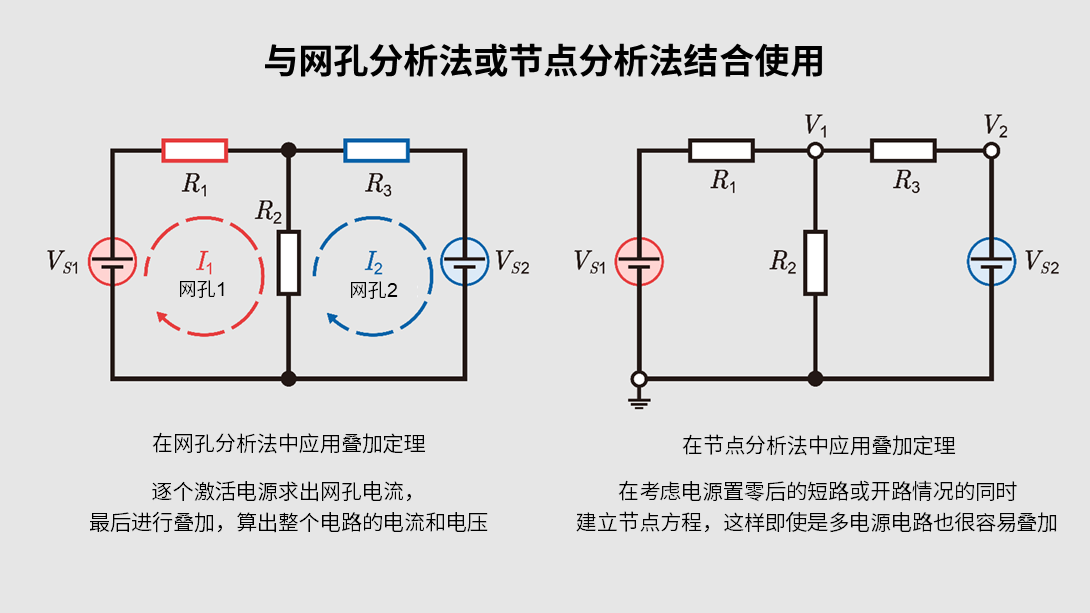
与网孔分析法或节点分析法结合使用
网孔分析法是一种应用基尔霍夫电压定律,为每个回路建立方程组的方法。应用叠加定理时,需逐个激活电路中的电源,并同步建立网孔方程。最后将每个电源求得的网孔电流进行叠加,即可得到整个电路的电流和电压。
节点分析法是先选定一个参考节点(接地点),然后以其他节点电位作为变量,再运用基尔霍夫电流定律来建立方程组的方法。同样地,若应用叠加定理,在考虑置零后的电源变为短路或开路的同时建立节点方程,那么即使是含多个电源的电路也更容易进行叠加。
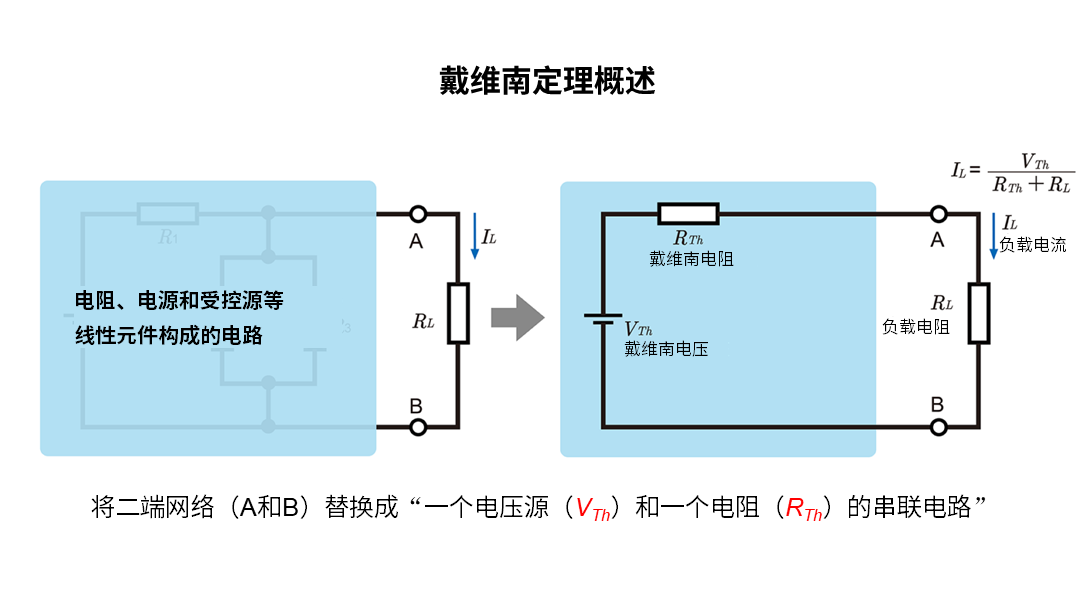
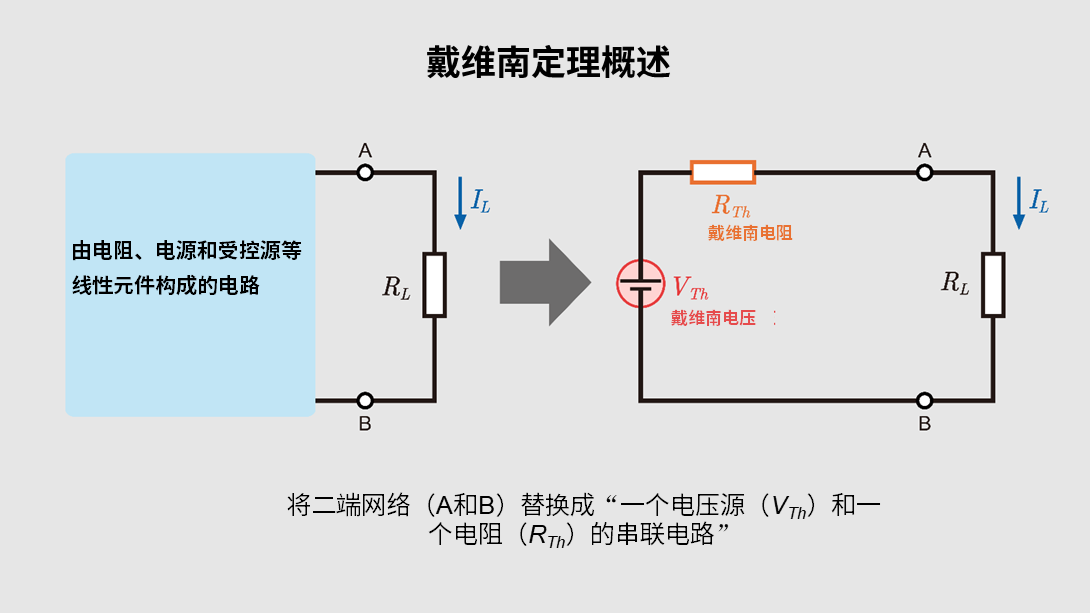
与戴维南等效电路的互补运用
戴维南定理是一种通过将电路的一部分替换为一个电压源和一个串联电阻,从而使从外部观察时的电路状态得以简化的方法。将其与叠加定理结合使用,可以更高效地进行电路分析。例如,当电路中含有多个独立电源时,通过分别考虑每个电源,并将其整合成戴维南等效电路后再进行叠加,可以简单地预测各种负载变化时的电压和电流特性。
叠加定理在电路设计中发挥作用的原因
叠加定理虽然常被认为是教科书里的基础理论,但在实际的电路设计工作中也有广泛的应用场景。
将多电源引发的复杂影响可视化
在AC电路、高频电路、以及包含多个DC电源的控制电路等场景中,每个电源对电路元件的影响各不相同。运用叠加定理可以分别确定每个独立电源流过的电流和产生的电压,因此非常有助于进行布局设计和故障分析。
设计阶段的验证和调试
在SPICE等电路分析工具内部,也利用了线性叠加定理。当试制电路板出现意外问题时,通过逐个启动电源进行测量,并与通过叠加定理预测的计算结果进行比较,可以更快地定位是由哪个电源引起的故障。
叠加定理的优势和局限性
叠加定理虽然非常有用,但并非是万能的。本节将对其优点、缺点和注意事项进行梳理。
| 优势 | 局限性 |
|---|---|
|
|
叠加定理在交流电路和相位分析中的应用
以上我们主要以直流电路为中心进行了说明,但只要电路是线性的,叠加定理也可以应用于交流电路。不过需要额外注意相位和频率的处理。
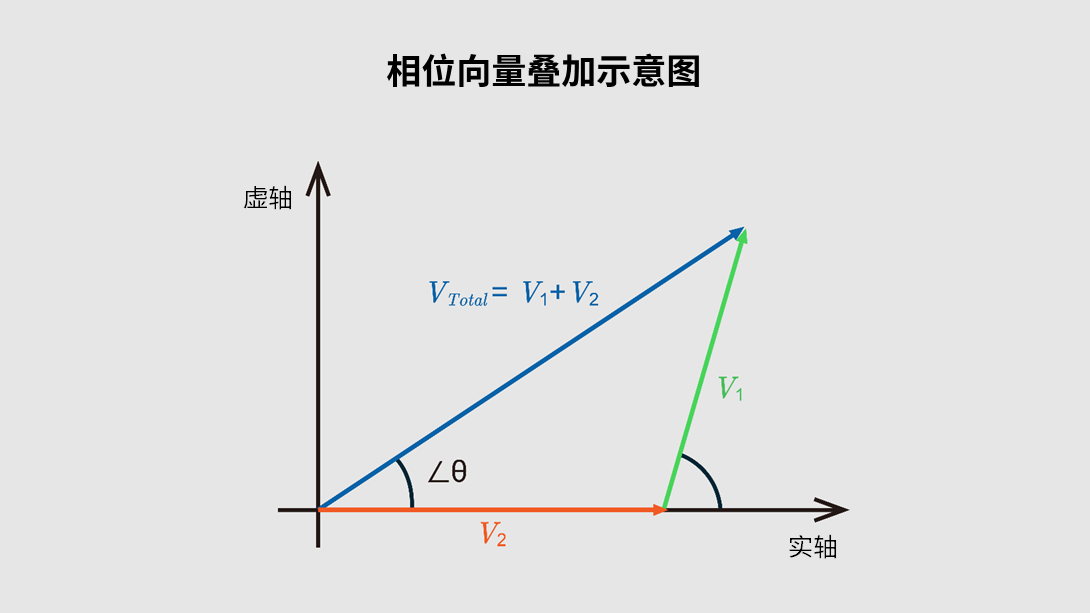
频率相同时的相位
当多个AC电源的频率相同仅相位不同时,采用复数表示法将其作为向量进行叠加,即可求得振幅和相位。应用叠加定理时,同样只保留一个电源,将其他电源视为0V,计算此时的相量,最后进行向量叠加即可。
频率不同时
当同时处理频率不同的电源时,不能简单地将向量的相位进行叠加。需要先按频率进行分离,然后转换回时域,或进行频谱分析。只要具有线性特性,叠加定理便依然适用,但在实际设计中,由于需要考虑滤波器和频率特性,因此通常只能部分应用该原理。
非线性元件及特殊电路中的注意事项
叠加定理基于线性特性,因此在实际电路中需要注意不可避免的非线性元件和特殊结构。
二极管和晶体管的大信号工作区
二极管具有正向电压近乎恒定的特性,而晶体管在大信号工作区也呈非线性工作。这样一来,在仅开启单一电源与开启多个电源的不同状态下,元件的工作点会发生很大变化,导致简单的叠加不再适用。此时,需要使用SPICE仿真或直接求解微分方程等方法。
含受控源的线性电路
受控源的输出会随某个电压或电流成比例变化,因此乍看之下似乎是非线性的,但只要其控制方程是线性的,就可以应用叠加定理。不过需要注意的是即使将独立电源关闭,也不能消除受控源本身。受控源会根据控制变量而动作,因此其处理方式与“短路”和“开路”不同。
电路分析中的代表性公式和中间计算
本节将对应用叠加定理时的常见公式和计算过程进行总结。串并联电阻的合成以及网孔分析法和节点分析法中的方程建立等都是典型示例。此处所列的公式不应死记硬背,更重要的是在正确理解电路结构的基础上加以运用。
串并联电阻的整合方法
在仅激活一个电源后,电路中剩余的电阻网络可以通过以下公式简化。
\(R_{series}=R_a+R_b+⋯\)
\(R_{parallel}=\displaystyle \frac{1}{\displaystyle \frac{1}{R_a}+\displaystyle \frac{1}{R_b}+⋯}\)
例如,若电路结构为\(R_2\)和\(R_3\)并联,其整体再与\(R_1\)串联,则可以先计算\(R_2\)‖\(R_3\),再叠加\(R_1\)得出总电阻。
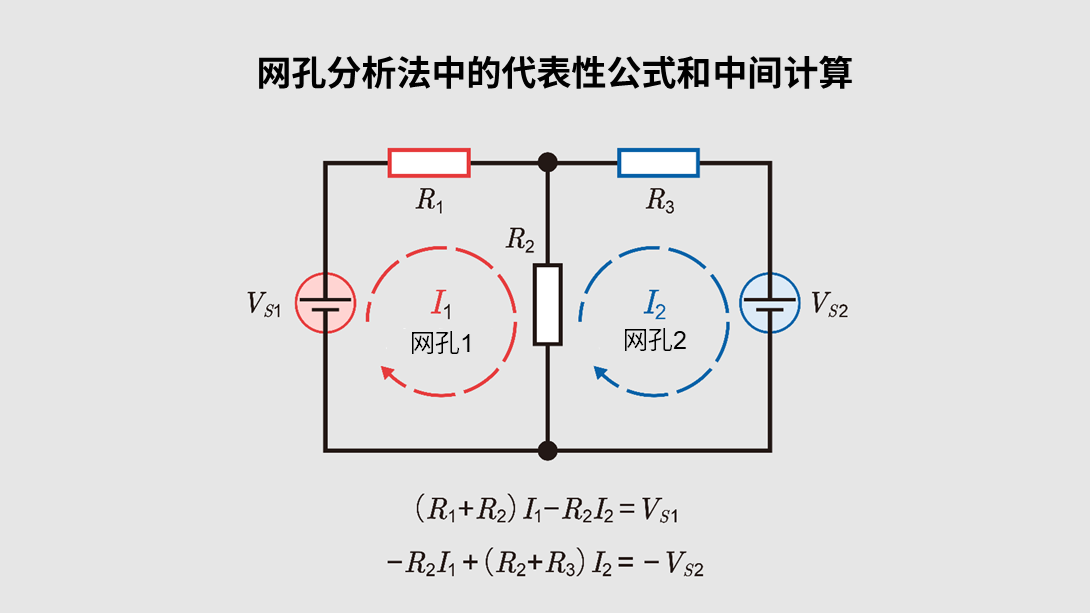
网孔分析法(回路分析法)示例
在网孔分析法中,需设定流经每个回路的电流\(I_1\), \(I_2\),……,再应用基尔霍夫电压定律建立方程组。当有两个网孔时,方程可能如下所示:
\((R_1+R_2 ) I_1-R_2 I_2=V_{s1}\)
\(- R_2 I_1+(R_2+R_3) I_2=-V_{s2}\)
要应用叠加定理,可以例如仅保留\(V_{S1}\),将\(V_{S2}\)视为0求解,再反过来进行求解,最后将两次的解叠加即可得到最终的\(I_1\)和\(I_2\)。
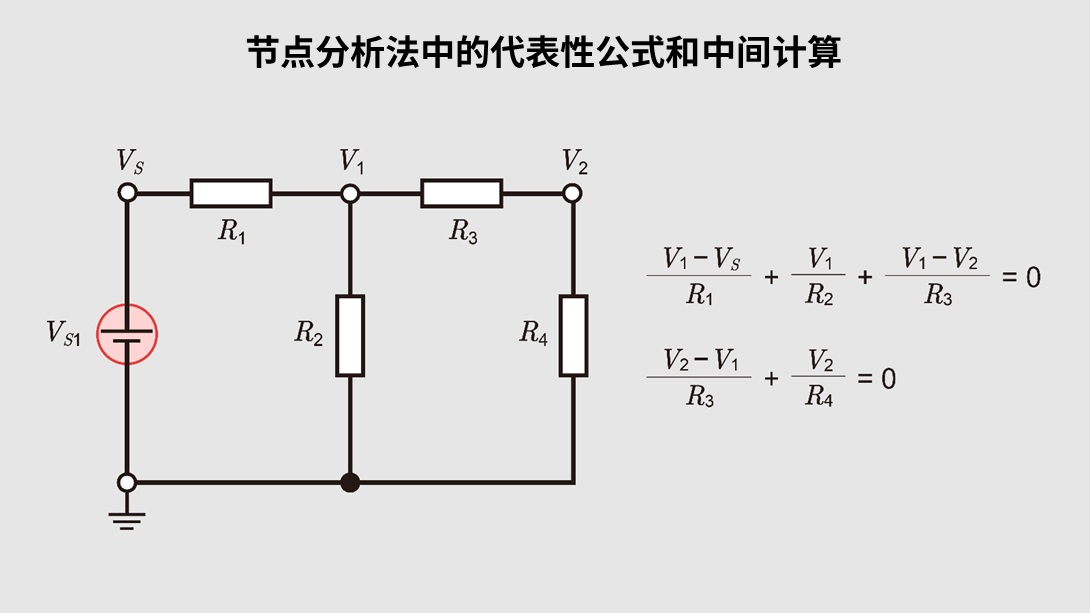
节点分析法(结点分析法)示例
在节点分析法中,将接地点设为0V,其余节点设为\(V_1\), \(V_2\),……,并应用基尔霍夫电流定律。例如,以含有\(V_1\)和\(V_2\)两个节点的简单电路为例:
\(\displaystyle \frac{V_1-V_s}{R_1}+\displaystyle \frac{V_1}{R_2}+\displaystyle \frac{V_1-V_2}{R_3} =0\)
\(\displaystyle \frac{V_2-V_1}{R_3}+\displaystyle \frac{V_2}{R_4}=0\)
此时,同样仅激活一个电源,将其他电源替换为短路或开路来建立方程,最后进行叠加。
对于电路设计人员的实际优势
叠加定理并不局限于教科书中的练习题,在实际的设计场景中往往也很方便实用。本节将从实际业务角度出发,对其具体优势进行梳理。
工作模式的分离和调试
在多个电源具有不同功能的系统(例如数字电路的5V电源和模拟电路的12V电源等)中,可以更轻松地分离每个电源的影响。特别是在调查具体是哪个电源引发的问题时,将叠加定理作为理论依据,故障排查会变得更加顺畅。
局部电路和试制评估中的应用
在大规模LSI或复杂系统中,若同时开启所有电源,可能会导致过电流或振荡。如果分阶段上电,并在确认各模块的工作状态时,将利用叠加定理算出的理论值与实际设备的测量值进行比较,可以大大提高快速定位故障点的可能性。
历史与发明者
最后,我们简要介绍一下叠加定理是在何时以及何种背景下确立的。电路理论的基础研究大约在19世纪开始蓬勃发展,欧姆定律和基尔霍夫电压定律也是在同一时期得以确立的。叠加定理本身是基于线性特性的数学思想,据说是在19世纪后半叶才逐渐传播开来的。关于具体是谁最先提出这个定理的,有许多说法,但随着电磁学和电路理论的发展,众多学者参与其中,逐步形成了如今的理论框架。
总结
本文从叠加定理的概述开始,详细介绍了其步骤、在电路设计中的应用示例以及与网孔分析法、节点分析法和戴维南等效电路等方法的结合使用等内容。文章的核心要点归纳如下:
- 在线性电路中,只要分别计算每个独立电源的响应,并将其进行叠加,就能求出整个电路的电压和电流
- 叠加定理很难直接应用于非线性元件和功率计算
- 在实际设计中,有助于将多个电源相互干扰的位置进行分离与定位,对调试和高精度设计也有很大帮助
- 若与网孔分析法、节点分析法和戴维南等效电路等其他方法结合使用,可以轻松地处理更复杂的电路问题
对于初学者来说,有助于理解含多个电源的电路特性,同时对于经验丰富的工程师而言,将每个电源分开来分析也往往比同时考虑所有电源更清晰易懂。希望本文能为您在应用叠加定理进行高效电路分析以及设计优化方面提供一些帮助。