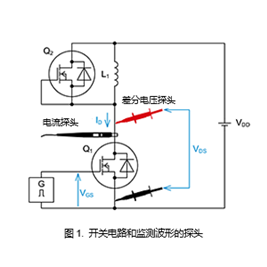
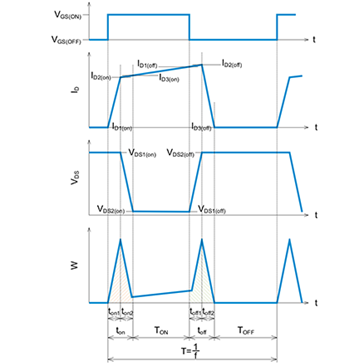
开关波形的测量方法
首先是开关波形的测量方法。近年来,一些示波器已经具备可以自动计算并显示所观测波形的功率损耗的功能,但如果没有该功能,就需要通过测得的波形来计算损耗了。为此,需要了解具体的测量方法和波形。
图1是开关电路、监测波形的探头以及测量示意图。我们使用差分探头来测量MOSFET的漏-源电压。另外,使用电流探头来测量漏极电流。
图2为各部分的波形和功率损耗(阴影区域)示意图。
\(t_{on}\)表示开通时间,\(t_{off}\)表示关断时间,在该区间的\(V_{DS}\)和\(I_D\)重叠部分产生了开关损耗。由于该电路是感性负载,因此在开通时,\(I_D\)会先开始变化,电流变化结束后\(V_{DS}\)开始变化。关断时则相反,\(V_{DS}\)先开始变化,电压变化结束后\(I_D\)才开始变化。
\(t_{on}\)是MOSFET的导通区间,在该区间中,会因\(I_D\)和MOSFET的导通电阻而产生导通损耗。
在进行测量时有一些注意事项。第一个是示波器的采样率。如果采样率过低,就会漏掉波形的细节部分,从而导致测量结果出现误差。因此需要显示采样点并确认是否是准确跟踪而获得的波形。
第二个是在电压探头和电流探头之间,由于延迟时间特性不同,所以测得的波形会因这种延迟差而存在误差。如果不进行任何校正,电压和电流之间就会在时间轴方向上出现偏差,图2阴影区域的面积就会不准确,从而导致损耗计算出现误差。要消除测量过程中的延迟差,就需要实施偏差校准(de-skew)。具体方法请参阅测量设备的使用说明书和测量设备制造商提供的技术资料。
除此之外,在处理测量点和探头操作等方面,请遵循对高电压和大电流进行高速开关的MOSFET的波形观测基本要求进行。
通过波形的线性近似法计算损耗的方法
下面将介绍根据前面测得的开关波形,使用线性近似法来计算功率损耗的方法。通过在线性近似有效范围内对所测得的波形进行分割,可以计算出功率损耗。
开通和关断区间的开关损耗
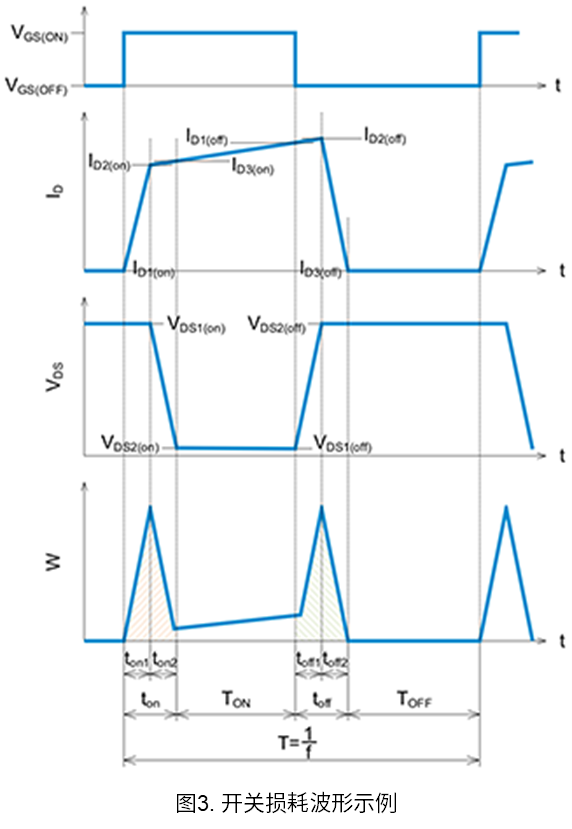
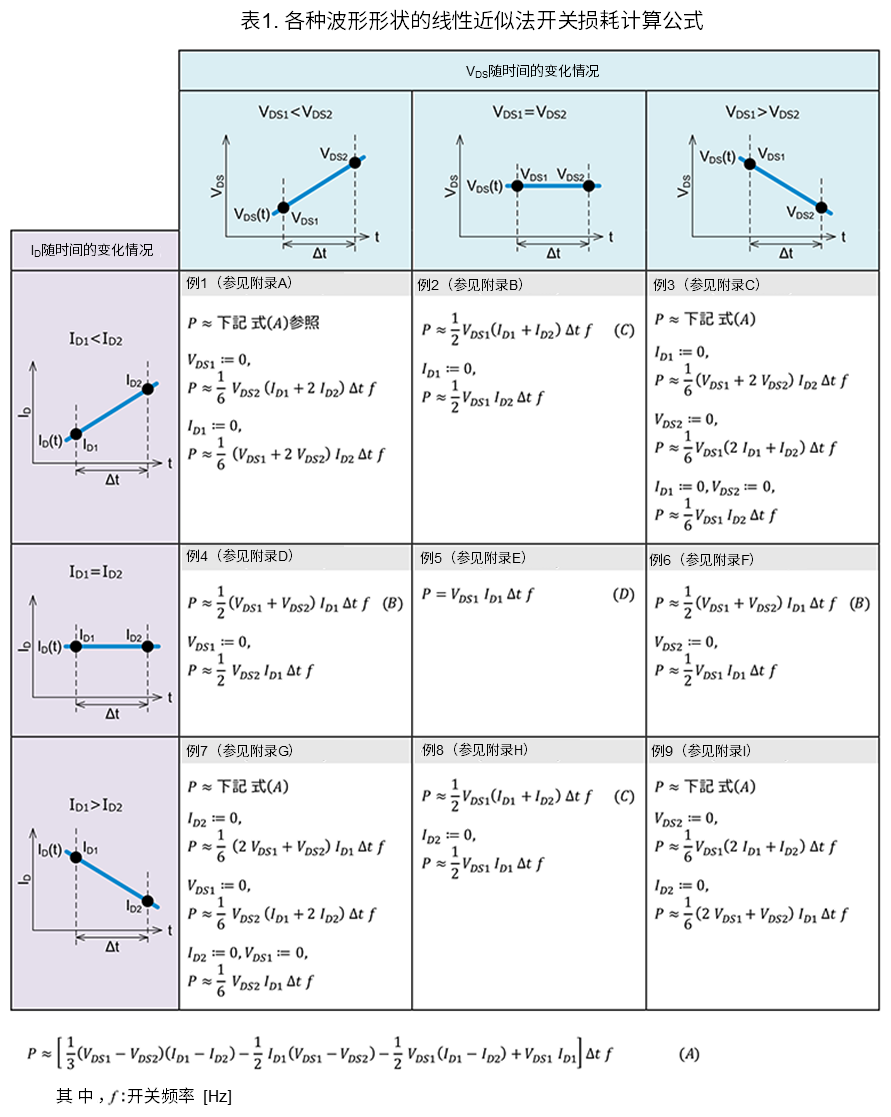
首先,计算开通和关断时间内消耗的功率损耗\(Pt_{on}\)和\(Pt_{off}\)。波形使用图3中的示例波形。功率损耗使用表1中的近似公式来计算。由于计算公式会因波形的形状而有所不同,因此请选择接近测得波形的近似公式。
在图3的波形示例中,开通时的波形被分割为两部分,前半部分(\(t_{on1}\))使用表1中的例2。另外,使用公式\(I_{D1}≔0\)作为条件。后半部分(\(t_{on2}\))使用例3中的公式\(V_{DS2}≔0\)。
在图3中,会因MOSFET的导通电阻和ID而产生电压\(V_{\mathrm{DS2(on)}}\),但如果该电压远低于、\(V_{DS}\)的High电压,就可以视其为零。综上所述,可以使用下面的公式(1)来近似计算开通时的功率损耗。
\(P_{\mathrm{ton}}\approx\displaystyle \frac{1}{2}V_{\mathrm{DS1(on)}}I_{\mathrm{D2(on)}}t_{\mathrm{on1}}f\)
\(+ \displaystyle \frac{1}{6} V_{DS1(\text{on})} \left( 2I_{D2(\text{on})} + I_{D3(\text{on})} \right) t_{\text{on2}} f\) (1)
同样,将关断时的波形也分为两部分,前半部分(\(t_{\mathrm{off1}}\))使用表1的例1中的公式\(V_{DS1}≔0\),后半部分(\(t_{\mathrm{off2}}\))使用例8中的公式\(I_{D2}≔0\)。在图3中,由于前述的原因,会产生电压\(V_{\mathrm{DS1(off)}}\),但如果该电压远低于\(V_{DS}\)的High电压,则将其按“零”处理。这样,就可以使用下面的公式(2)来近似计算关断时的功率损耗。
\(P_{\mathrm{toff}}\approx\displaystyle \frac{1}{6}V_{\mathrm{DS2(off)}}\left(I_{\mathrm{D1(off)}}+2I_{\mathrm{D2(off)}}\right)t_{\mathrm{off1}}f\)
\(+\displaystyle \frac{1}{2}V_{\mathrm{DS2(off)}}I_{\mathrm{D2(off)}}t_{\mathrm{off2}}f\) (2)
导通期间的功率损耗
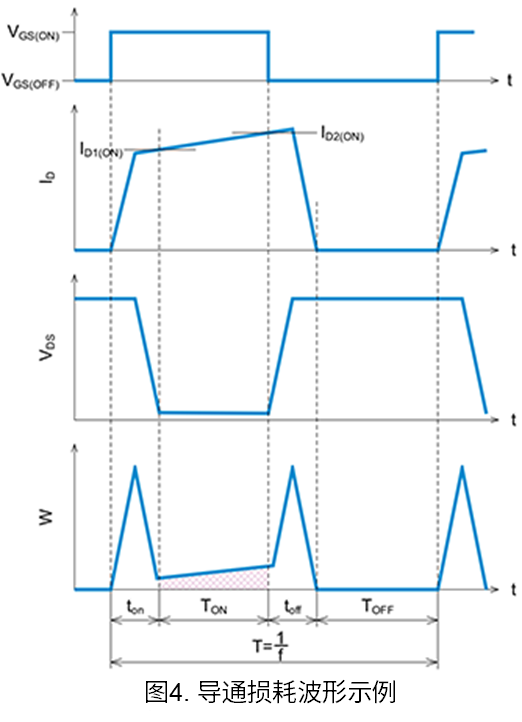
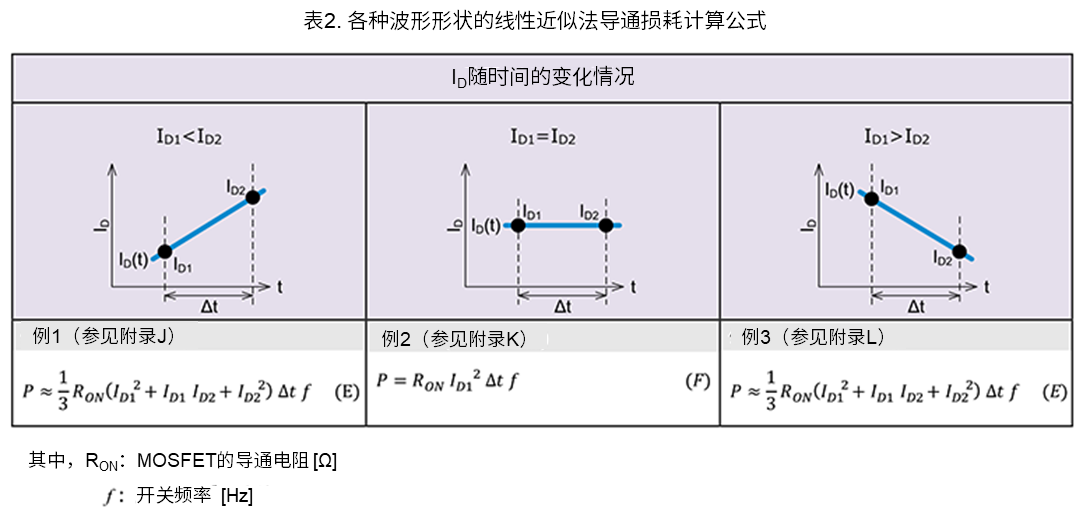
接下来,我们来计算导通期间消耗的功率损耗。图4是用来计算导通损耗的波形示例。由于在\(T_{ON}\)区间MOSFET是导通的,因此、\(V_{DS}\)是MOSFET导通电阻和\(I_D\)的乘积。有关导通电阻的值,请参阅技术规格书。需要从表2中选择接近该波形形状的例子并使用其近似公式来计算功率损耗。
在本示例中,我们使用表2中的例1。MOSFET导通期间的导通损耗可以用下面的公式(3)来计算。
\(P_{\mathrm{ON}}\approx\displaystyle \frac{1}{3}R_{\mathrm{ON}}\left(I_{\mathrm{D1(ON)}}^2+I_{\mathrm{D1(ON)}}I_{\mathrm{D2(ON)}}+I_{\mathrm{D2(ON)}}^2\right)T_{\mathrm{ON}}f\) (3)
MOSFET关断时的功率损耗在图4中位于\(T_{OFF}\)区间,由于MOSFET关断时的\(I_D\)足够小,因此将功率损耗视为零。
总损耗
如公式(4)所示,MOSFET开关工作时的总功率损耗为此前计算出的开关损耗和导通损耗之和。
\(P_D = P_{ton} + P_{toff} + P_{ON} \, [\mathrm{W}] \) (4)
需要注意的是,表1和表2中的每个例子都有“参见附录”的注释,在附录中有每个例子的详细计算示例。各计算示例将会在后续的“各种波形的开关损耗计算示例”和“各种波形的导通损耗计算示例”中出现。
根据测得波形计算功率损耗示例
接下来,我们将使用“通过波形的线性近似分割来计算损耗的方法”,根据所测得的波形来计算功率损耗(示例)。
下面我们通过示例,来根据实际测得的开关波形计算功率损耗。图5是实测的开关波形,显示了反复进行ON/OFF时的整体情况。波形图中上方是\(I_D\)的波形,下方是\(V_{DS}\)的波形。下面我们根据该波形,来分别计算开通(开关接通)时、导通时(导通状态)和关断(开关关闭)时的损耗。
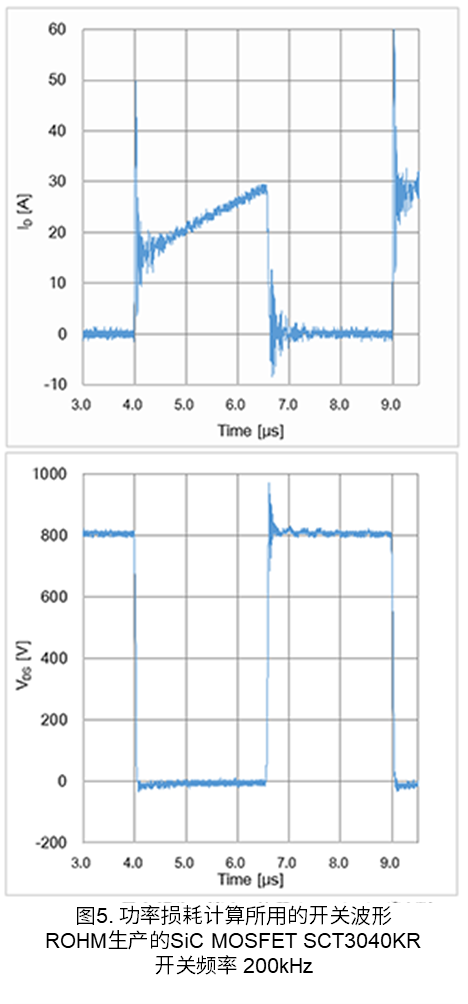
开通时的损耗计算
图6是图5中开通时的波形放大图,需要使用\(I_D\)(上)和\(V_{DS}\)(下)来计算损耗。由于在波形过程中的斜率发生了变化,因此需要按相同的斜率来分割区间,但由于波形很复杂,因此区间分割是主观的。读取每个区间的起始电压和电流、终止电压和电流以及时间。
将值代入“通过波形的线性近似分割来计算损耗的方法”中的表1中列出的公式(A),求出功率损耗。在这之后我们都将按照表1中给出的公式进行计算,所以请您参考表1阅读下面的内容。图6右侧是开关开通时的功率损耗计算示例。在这里将分割的区间命名为t1~t5。
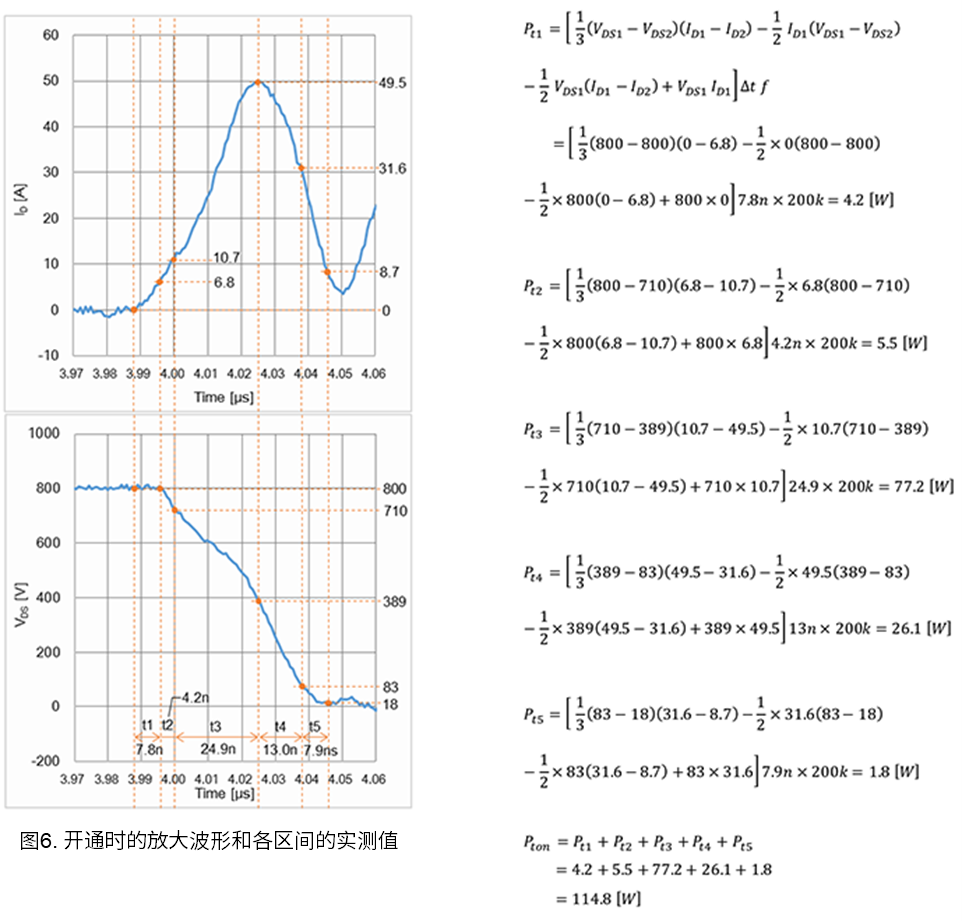
如最后一个公式\(Pt_{on}\)所示,开通时的损耗是分割区间t1~t5损耗的总和。
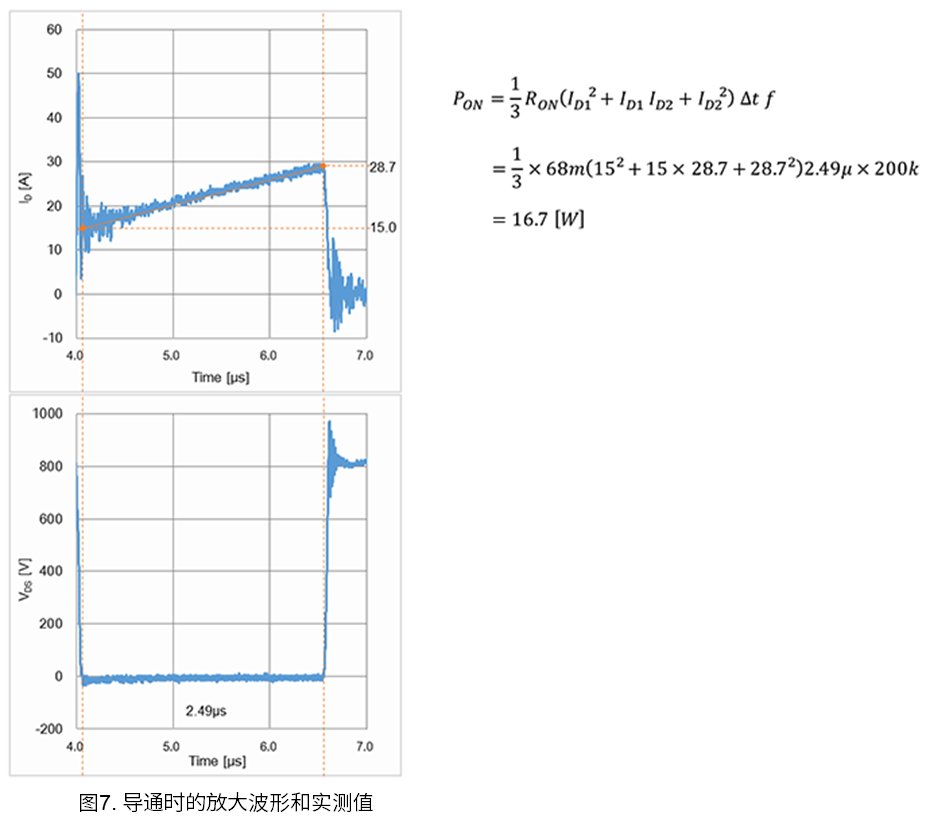
导通时的损耗计算
图7是导通时的放大波形。导通时的损耗计算也是一样,通过将值带入“通过波形的线性近似分割来计算损耗的方法”中的表2中的公式(E)来计算。关于SiC MOSFET的导通电阻,需要使用技术规格书中给出的最大值。
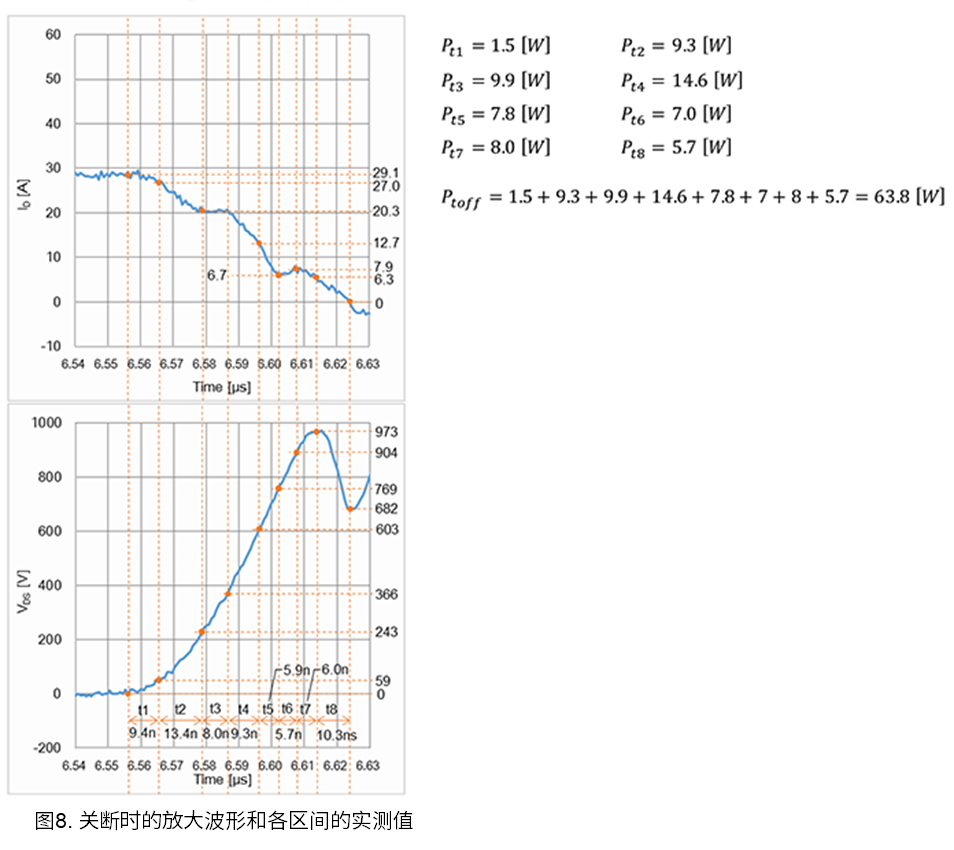
关断时的损耗计算
图8是关断时的波形放大图。关断时的损耗计算方法与开通时的相同,将值代入表1中的公式(A)来计算。在这里将分割的区间命名为t1~t8。图中给出了关断时每个区间的损耗计算结果以及关断时的损耗(\(Pt_{off}\)=各区间的损耗之和)。
总功率损耗的计算
总功率损耗可以通过下面的公式计算。如公式所示,总功率损耗是上面求得的开通损耗、导通损耗和关断损耗之和。
\(P = P_{\mathrm{ton}} + P_{\mathrm{ON}} + P_{\mathrm{toff}} \\
= 114.8 + 16.7 + 63.8 \\
= 195.3 \, \left[\mathrm{W}\right]\)
各种波形的开关损耗计算示例
在“根据测得波形计算功率损耗示例”中,作为示例,我们将实测波形在线性近似有效范围内进行分割,并使用“通过波形的线性近似分割来计算损耗的方法”中相应的公式,计算了开关损耗和导通损耗,并计算了总损耗。
从本文开始,我们将利用“通过波形的线性近似分割来计算损耗的方法”的表1中给出的所有基于线性近似分割来计算开关损耗的公式,计算1~9种情况(附录A~I)下的开关损耗(示例)。对于使用“根据测得波形计算功率损耗示例”中没有的公式计算开关损耗的情况,请参考下面的链接。另外,使用表2所示的线性近似分割方法来计算导通损耗的公式进行计算的示例,会另行发布,届时请一并参阅。
各种波形的开关损耗计算示例
- 例1:\(I_D\)上升、\(V_{DS}\)上升波形(附录A)
- 例2:\(I_D\)上升、\(V_{DS}\)恒定波形(附录B)
- 例3:\(I_D\)上升、\(V_{DS}\)下降波形(附录C)
- 例4:\(I_D\)恒定、\(V_{DS}\)上升波形(附录D)
- 例5:\(I_D\)恒定、\(V_{DS}\)恒定波形(附录E)
- 例6:\(I_D\)恒定、\(V_{DS}\)下降波形(附录F)
- 例7:\(I_D\)下降、\(V_{DS}\)上升波形(附录G)
- 例8:\(I_D\)下降、\(V_{DS}\)恒定波形(附录H)
- 例9:\(I_D\)下降、\(V_{DS}\)下降波形(附录I)
各种波形的开关损耗计算示例:例1:\(I_D\)上升、\(V_{DS}\)上升波形(附录A)
下面我们根据开关波形的漏-源电压\(V_{DS}\)和漏极电流\(I_D\),使用线性近似方式计算开通时和关断时的功率损耗(开关损耗)。图A-1是用于损耗计算的波形。
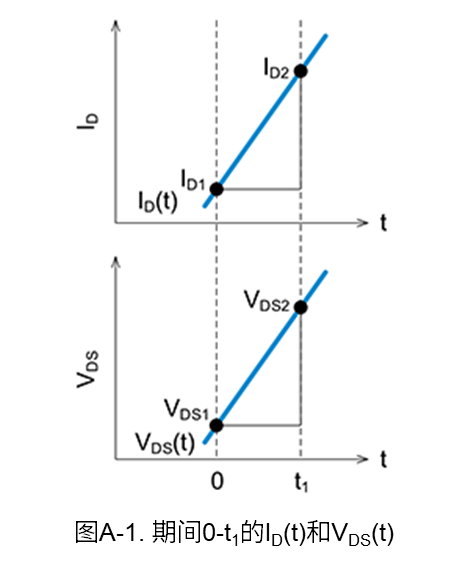
图A-1中0-t1期间的功率损耗\(P\),通常可以通过对公式(A-1)中的电流和电压之积进行积分来计算。
\(P = f \int_{0}^{t_1} I_D(t) V_{\mathrm{DS}}(t) \, dt\) (A-1)
其中,\(f\):开关频率[Hz]
另外,\(I_{D(t)}\)和\(V_{DS(t)}\)可根据图A-1中的斜率,用公式(A-2)和公式(A-3)来表示。
\(I_D\left(t\right)=I_{D1}+\displaystyle \frac{I_{D2}-I_{D1}}{t_1}t=I_{D1}-\displaystyle \frac{I_{D1}-I_{D2}}{t_1}t\) (A-2)
\(V_{\mathrm{DS}}\left(t\right)=V_{\mathrm{DS1}}+\displaystyle \frac{V_{\mathrm{DS2}}-V_{\mathrm{DS1}}}{t_1}t=V_{\mathrm{DS1}}-\displaystyle \frac{V_{\mathrm{DS1}}-V_{\mathrm{DS2}}}{t_1}t\) (A-3)
将公式(A-2)和公式(A-3)代入公式(A-1),
\(P=f\int_{0}^{t_1}\left(I_{D1}-\displaystyle \frac{I_{D1}-I_{D2}}{t_1}t\right)\left(V_{\mathrm{DS1}}-\displaystyle \frac{V_{\mathrm{DS1}}-V_{\mathrm{DS2}}}{t_1}t\right)dt\) (A-4)
\(=f\int_{0}^{t_1}\left(V_{\mathrm{DS1}}I_{D1}-\displaystyle \frac{I_{D1}\left(V_{\mathrm{DS1}}-V_{\mathrm{DS2}}\right)+V_{\mathrm{DS1}}\left(I_{D1}-I_{D2}\right)}{t_1}t+\displaystyle \frac{\left(V_{\mathrm{DS1}}-V_{\mathrm{DS2}}\right)\left(I_{D1}-I_{D2}\right)}{t_1^2}t^2\right)dt\) (A-5)
根据公式进行积分。
\(P=f\left[V_{\mathrm{DS1}}I_{D1}t-\displaystyle \frac{1}{2}\displaystyle \frac{I_{D1}\left(V_{\mathrm{DS1}}-V_{\mathrm{DS2}}\right){+V}_{\mathrm{DS1}}\left(I_{D1}-I_{D2}\right)}{t_1}t^2+\displaystyle \frac{1}{3}\displaystyle \frac{\left(V_{\mathrm{DS1}}-V_{\mathrm{DS2}}\right)\left(I_{D1}-I_{D2}\right)}{t_1^2}t^3\right]_0^{t_1}\) (A-6)
\(=f\left[V_{\mathrm{DS1}}I_{D1}t_1-\displaystyle \frac{1}{2}\displaystyle \frac{I_{D1}\left(V_{\mathrm{DS1}}-V_{\mathrm{DS2}}\right){+V}_{\mathrm{DS1}}\left(I_{D1}-I_{D2}\right)}{t_1}t_1^2+\displaystyle \frac{1}{3}\displaystyle \frac{\left(V_{\mathrm{DS1}}-V_{\mathrm{DS2}}\right)\left(I_{D1}-I_{D2}\right)}{t_1^2}t_1^3\right]\) (A-7)
\(=f\left[V_{\mathrm{DS1}}I_{D1}t_1-\displaystyle \frac{1}{2}\left(I_{D1}\left(V_{\mathrm{DS1}}-V_{\mathrm{DS2}}\right)+V_{\mathrm{DS1}}\left(I_{D1}-I_{D2}\right)\right)t_1+\displaystyle \frac{1}{3}\left(V_{\mathrm{DS1}}-V_{\mathrm{DS2}}\right)\left(I_{D1}-I_{D2}\right)t_1\right]\) (A-8)
\(= \left[ \displaystyle \frac{1}{3} (V_{DS1} – V_{DS2})(I_{D1} – I_{D2}) – \displaystyle \frac{1}{2} I_{D1} (V_{DS1} – V_{DS2}) – \displaystyle \frac{1}{2} V_{DS1} (I_{D1} – I_{D2}) + V_{DS1} I_{D1} \right] t_1 f\) (A-9)
其中,\(f\):开关频率[Hz]
求下列条件下的功率损耗。
・\(\underline{V_{DS1}≔0}\) (A-10)
将公式(A-10)代入公式(A-9)。
\(P=\left[\displaystyle \frac{1}{3}\left(0-V_{\mathrm{DS2}}\right)\left(I_{D1}-I_{D2}\right)-\displaystyle \frac{1}{2}I_{D1}\left(0-V_{\mathrm{DS2}}\right)-\displaystyle \frac{1}{2}\times0\left(I_{D1}-I_{D2}\right)+0\times I_{D1}\right]t_1f\) (A-11)
\(=\left[-\displaystyle \frac{1}{3}V_{\mathrm{DS2}}\left(I_{D1}-I_{D2}\right)+\displaystyle \frac{1}{2}I_{D1}V_{\mathrm{DS2}}\right]t_1f\) (A-12)
\(= \displaystyle \frac{1}{6} V_{DS2} (I_{D1} + 2I_{D2}) t_1 f \, [W]\) (A-13)
・\(\underline{I_{D1}≔0}\) (A-14)
将公式(A-14)代入公式(A-9)。
\(P=\left[\displaystyle \frac{1}{3}\left(V_{\mathrm{DS1}}-V_{\mathrm{DS2}}\right)\left(0-I_{D2}\right)-\displaystyle \frac{1}{2}\times0\left(V_{\mathrm{DS1}}-V_{\mathrm{DS2}}\right)-\displaystyle \frac{1}{2}V_{\mathrm{DS1}}\left(0-I_{D2}\right)+V_{\mathrm{DS1}}\times0\right]t_1f\) (A-15)
\(=\left[\displaystyle \frac{1}{3}\left(V_{\mathrm{DS1}}-V_{\mathrm{DS2}}\right)\left(-I_{D2}\right)+\displaystyle \frac{1}{2}V_{\mathrm{DS1}}I_{D2}\right]t_1f\) (A-16)
\(= \displaystyle \frac{1}{6} (V_{DS1} + 2V_{DS2}) I_{D2} t_1 f \, [W] \) (A-17)
各种波形的开关损耗计算示例:例2:ID上升、VDS恒定波形(附录B)
下面我们根据开关波形的漏-源电压\(V_{DS}\)和漏极电流\(I_D\),使用线性近似方式计算开通时和关断时的功率损耗(开关损耗)。图B-1是用于损耗计算的波形。
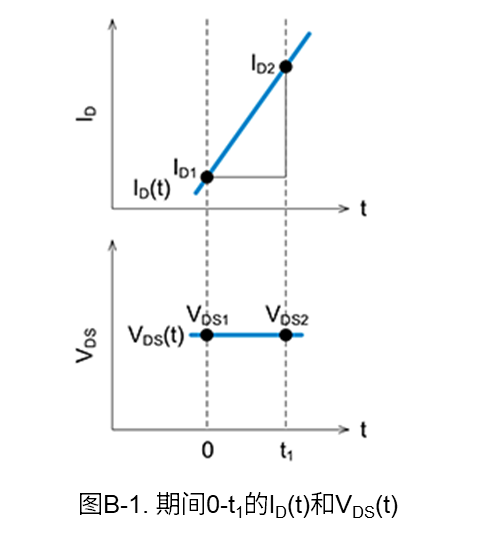
图B-1中0-t1期间的功率损耗\(P\),通常可以通过对公式(B-1)中的电流和电压之积进行积分来计算。
\(P = f \int_{0}^{t_1} I_D (t) V_{DS} (t) \, dt\) (B-1)
其中,\(f\):开关频率[Hz]
另外,\(I_{D(t)}\)和\(V_{DS(t)}\)可根据图B-1中的斜率,用公式(B-2)和公式(B-3)来表示。
\(I_D\left(t\right)=I_{D1}+\displaystyle \frac{I_{D2}-I_{D1}}{t_1}t=I_{D1}-\displaystyle \frac{I_{D1}-I_{D2}}{t_1}t\) (B-2)
\(V_{\mathrm{DS}}\left(t\right)=V_{\mathrm{DS1}}\) (B-3)
将公式(B-2)和公式(B-3)代入公式(B-1),
\(P = f \int_{0}^{t_1} \left( I_{D1} – \displaystyle \frac{I_{D1} – I_{D2}}{t_1} t \right) (V_{DS1}) \, dt\) (B-4)
\(= f \int_{0}^{t_1} \left( V_{DS1} I_{D1} – \displaystyle \frac{V_{DS1} (I_{D1} – I_{D2})}{t_1} t \right) dt\) (B-5)
根据公式进行积分。
\(P=f\left[V_{\mathrm{DS1}}I_{D1}t-\displaystyle \frac{1}{2}\displaystyle \frac{V_{\mathrm{DS1}}\left(I_{D1}-I_{D2}\right)}{t_1}t^2\right]_0^{t_1}\) (B-6)
\(=f\left[V_{\mathrm{DS1}}I_{D1}t_1-\displaystyle \frac{1}{2}\displaystyle \frac{V_{\mathrm{DS1}}\left(I_{D1}-I_{D2}\right)}{t_1}t_1^2\right]\) (B-7)
\(=f\left[V_{\mathrm{DS1}}I_{D1}t_1-\displaystyle \frac{1}{2}\left(V_{\mathrm{DS1}}\left(I_{D1}-I_{D2}\right)\right)t_1\right]\) (B-8)
\(= \displaystyle \frac{1}{2} V_{DS1} (I_{D1} + I_{D2}) t_1 f \, [W]\) (B-9)
求下列条件下的功率损耗。
・\(\underline{I_{D1}≔0}\) (B-10)
将公式(B-10)代入公式(B-9)。
\(P = \displaystyle \frac{1}{2} V_{DS1} I_{D2} t_1 f \, [W]\) (B-11)
各种波形的开关损耗计算示例:例3:\(I_D\)上升、\(V_{DS}\)下降波形(附录C)
下面我们根据开关波形的漏-源电压\(V_{DS}\)和漏极电流\(I_D\),使用线性近似方式计算开通时和关断时的功率损耗(开关损耗)。图C-1是用于损耗计算的波形。
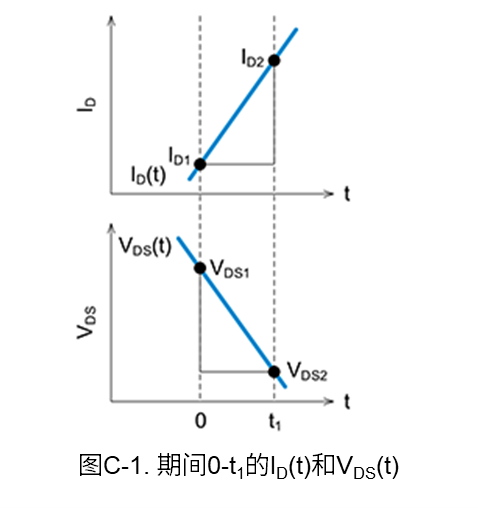
图C-1中0-t1期间的功率损耗\(P\),通常可以通过对公式(C-1)中的电流和电压之积进行积分来计算。
\(P = f \int_{0}^{t_1} I_D (t) V_{DS} (t) \, dt\) (C-1)
其中,\(f\):开关频率[Hz]
另外,\(I_{D(t)}\)和\(V_{DS(t)}\)可根据图C-1中的斜率,用公式(C-2)和公式(C-3)来表示。
\(I_D\left(t\right)=I_{D1}+\displaystyle \frac{I_{D2}-I_{D1}}{t_1}t=I_{D1}-\displaystyle \frac{I_{D1}-I_{D2}}{t_1}t\) (C-2)
\(V_{\mathrm{DS}}\left(t\right)=V_{\mathrm{DS1}}-\displaystyle \frac{V_{\mathrm{DS1}}-V_{\mathrm{DS2}}}{t_1}t\) (C-3)
将公式(C-2)和公式(C-3)代入公式(C-1),
\(P=f\int_{0}^{t_1}\left(I_{D1}-\displaystyle \frac{I_{D1}-I_{D2}}{t_1}t\right)\left(V_{\mathrm{DS1}}-\displaystyle \frac{V_{\mathrm{DS1}}-V_{\mathrm{DS2}}}{t_1}t\right)dt\) (C-4)
\(=f\int_{0}^{t_1}\left(V_{\mathrm{DS1}}I_{D1}-\displaystyle \frac{I_{D1}\left(V_{\mathrm{DS1}}-V_{\mathrm{DS2}}\right){+V}_{\mathrm{DS1}}\left(I_{D1}-I_{D2}\right)}{t_1}t+\displaystyle \frac{\left(V_{\mathrm{DS1}}-V_{\mathrm{DS2}}\right)\left(I_{D1}-I_{D2}\right)}{t_1^2}t^2\right)dt\) (C-5)
根据公式进行积分。
\(P=f\left[V_{\mathrm{DS1}}I_{D1}t-\displaystyle \frac{1}{2}\displaystyle \frac{I_{D1}\left(V_{\mathrm{DS1}}-V_{\mathrm{DS2}}\right){+V}_{\mathrm{DS1}}\left(I_{D1}-I_{D2}\right)}{t_1}t^2+\displaystyle \frac{1}{3}\displaystyle \frac{\left(V_{\mathrm{DS1}}-V_{\mathrm{DS2}}\right)\left(I_{D1}-I_{D2}\right)}{t_1^2}t^3\right]_0^{t_1}\) (C-6)
\(=f\left[V_{\mathrm{DS1}}I_{D1}t_1-\displaystyle \frac{1}{2}\displaystyle \frac{I_{D1}\left(V_{\mathrm{DS1}}-V_{\mathrm{DS2}}\right){+V}_{\mathrm{DS1}}\left(I_{D1}-I_{D2}\right)}{t_1}t_1^2+\displaystyle \frac{1}{3}\displaystyle \frac{\left(V_{\mathrm{DS1}}-V_{\mathrm{DS2}}\right)\left(I_{D1}-I_{D2}\right)}{t_1^2}t_1^3\right]\) (C-7)
\(=f\left[V_{\mathrm{DS1}}I_{D1}t_1-\displaystyle \frac{1}{2}\left(I_{D1}\left(V_{\mathrm{DS1}}-V_{\mathrm{DS2}}\right)+V_{\mathrm{DS1}}\left(I_{D1}-I_{D2}\right)\right)t_1+\displaystyle \frac{1}{3}\left(V_{\mathrm{DS1}}-V_{\mathrm{DS2}}\right)\left(I_{D1}-I_{D2}\right)t_1\right]\) (C-8)
\(= \left[ \displaystyle \frac{1}{3} (V_{DS1} – V_{DS2}) (I_{D1} – I_{D2}) – \displaystyle \frac{1}{2} I_{D1} (V_{DS1} – V_{DS2}) – \displaystyle \frac{1}{2} V_{DS1} (I_{D1} – I_{D2}) + V_{DS1} I_{D1} \right] t_1 f \, [W]\) (C-9)
求下列条件下的功率损耗。
・\(\underline{I_{D1}≔0}\) (C-10)
将公式(C-10)代入公式(C-9)。
\(P=\left[\displaystyle \frac{1}{3}\left(V_{\mathrm{DS1}}-V_{\mathrm{DS2}}\right)\left(0-I_{D2}\right)-\displaystyle \frac{1}{2}\times0\left(V_{\mathrm{DS1}}-V_{\mathrm{DS2}}\right)-\displaystyle \frac{1}{2}V_{\mathrm{DS1}}\left(0-I_{D2}\right)+V_{\mathrm{DS1}}\times0\right]t_1f\) (C-11)
\(=\left[\displaystyle \frac{1}{3}\left(V_{\mathrm{DS1}}-V_{\mathrm{DS2}}\right)\left(-I_{D2}\right)+\displaystyle \frac{1}{2}V_{\mathrm{DS1}}I_{D2}\right]t_1f\) (C-12)
\(= \displaystyle \frac{1}{6} (V_{DS1} + 2V_{DS2}) I_{D2} t_1 f \, [W]\) (C-13)
・\(\underline{V_{DS}2≔0}\) (C-14)
将公式(C-14)代入公式(C-9)。
\(P=\left[\displaystyle \frac{1}{3}\left(V_{\mathrm{DS1}}-0\right)\left(I_{D1}-I_{D2}\right)-\displaystyle \frac{1}{2}I_{D1}\left(V_{\mathrm{DS1}}-0\right)-\displaystyle \frac{1}{2}V_{\mathrm{DS1}}\left(I_{D1}-I_{D2}\right)+V_{\mathrm{DS1}}I_{D1}\right]t_1f\) (C-15)
\(=\left[\displaystyle \frac{1}{3}V_{\mathrm{DS1}}\left(I_{D1}-I_{D2}\right)-\displaystyle \frac{1}{2}I_{D1}V_{\mathrm{DS1}}-\displaystyle \frac{1}{2}V_{\mathrm{DS1}}\left(I_{D1}-I_{D2}\right)+V_{\mathrm{DS1}}I_{D1}\right]t_1f\) (C-16)
\(= \displaystyle \frac{1}{6} V_{DS1} (2I_{D1} + I_{D2}) t_1 f \, [W]\) (C-17)
・\(\underline{I_{D1}≔0,V_{DS2}≔0}\) (C-18)
将公式(C-18)代入公式(C-9)。
\(P=\left[\displaystyle \frac{1}{3}\left(V_{\mathrm{DS1}}-0\right)\left(0-I_{D2}\right)-\displaystyle \frac{1}{2}\times0\left(V_{\mathrm{DS1}}-0\right)-\displaystyle \frac{1}{2}V_{\mathrm{DS1}}\left(0-I_{D2}\right)+V_{\mathrm{DS1}}\times0\right]t_1f\) (C-19)
\(=\left[\displaystyle \frac{1}{3}V_{\mathrm{DS1}}\left(-I_{D2}\right)-\displaystyle \frac{1}{2}V_{\mathrm{DS1}}\left(-I_{D2}\right)\right]t_1f\) (C-20)
\(= \displaystyle \frac{1}{6} V_{DS1} I_{D2} t_1 f \, [W]\) (C-21)
各种波形的开关损耗计算示例:例4:\(I_D\)恒定、\(V_{DS}\)上升波形(附录D)
下面我们根据开关波形的漏-源电压\(V_{DS}\)和漏极电流\(I_D\),使用线性近似方式计算开通时和关断时的功率损耗(开关损耗)。图D-1是用于损耗计算的波形。
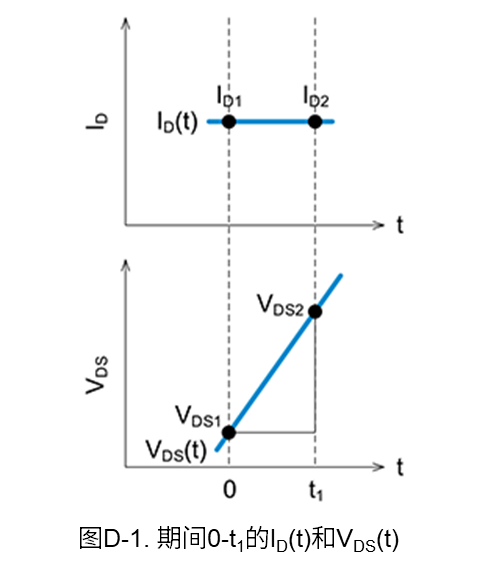
图D-1中0-t1期间的功率损耗\(P\),通常可以通过对公式(D-1)中的电流和电压之积进行积分来计算。
\(P = f \int_{0}^{t_1} I_D (t) V_{DS} (t) \, dt\) (D-1)
其中,\(f\):开关频率[Hz]
另外,\(I_{D(t)}\)和\(V_{DS(t)}\)可根据图D-1中的斜率,用公式(D-2)和公式(D-3)来表示。
\(I_D\left(t\right)=I_{D1}\) (D-2)
\(V_{\mathrm{DS}}\left(t\right)=V_{\mathrm{DS1}}+\displaystyle \frac{V_{\mathrm{DS2}}-V_{\mathrm{DS1}}}{t_1}t=V_{\mathrm{DS1}}-\displaystyle \frac{V_{\mathrm{DS1}}-V_{\mathrm{DS2}}}{t_1}t\) (D-3)
将公式(D-2)和公式(D-3)代入公式(D-1),
\(P=f\int_{0}^{t_1}{I_{D1}\left(V_{\mathrm{DS1}}-\displaystyle \frac{V_{\mathrm{DS1}}-V_{\mathrm{DS2}}}{t_1}t\right)dt}\) (D-4)
\(=f\int_{0}^{t_1}\left(V_{\mathrm{DS1}}I_{D1}-\displaystyle \frac{I_{D1}\left(V_{\mathrm{DS1}}-V_{\mathrm{DS2}}\right)}{t_1}t\right)dt\) (D-5)
根据公式进行积分。
\(P=f\left[V_{\mathrm{DS1}}I_{D1}t-\displaystyle \frac{1}{2}\displaystyle \frac{I_{D1}\left(V_{\mathrm{DS1}}-V_{\mathrm{DS2}}\right)}{t_1}t^2\right]_0^{t_1}\) (D-6)
\(=f\left[V_{\mathrm{DS1}}I_{D1}t_1-\displaystyle \frac{1}{2}\displaystyle \frac{I_{D1}\left(V_{\mathrm{DS1}}-V_{\mathrm{DS2}}\right)}{t_1}t_1^2\right]\) (D-7)
\(=f\left[V_{\mathrm{DS1}}I_{D1}t_1-\displaystyle \frac{1}{2}\left(I_{D1}\left(V_{\mathrm{DS1}}-V_{\mathrm{DS2}}\right)\right)t_1\right]\) (D-8)
\(=\displaystyle \frac{1}{2}\left(V_{\mathrm{DS1}}+V_{\mathrm{DS2}}\right)I_{D1}t_1f W\) (D-9)
求下列条件下的功率损耗。
・\(\underline{V_{DS1}≔0}\) (D-10)
将公式(D-10)代入公式(D-9)。
\(P=\displaystyle \frac{1}{2}\left(0+V_{\mathrm{DS2}}\right)I_{D1}t_1f\) (D-11)
\(= \displaystyle \frac{1}{2} V_{DS2} I_{D1} t_1 f \, [W]\) (D-12)
各种波形的开关损耗计算示例:例5:\(I_D\)恒定、\(V_{DS}\)恒定(附录E)
下面我们根据开关波形的漏-源电压\(V_{DS}\)和漏极电流\(I_D\),使用线性近似方式计算开通时和关断时的功率损耗(开关损耗)。图E-1是用于损耗计算的波形。
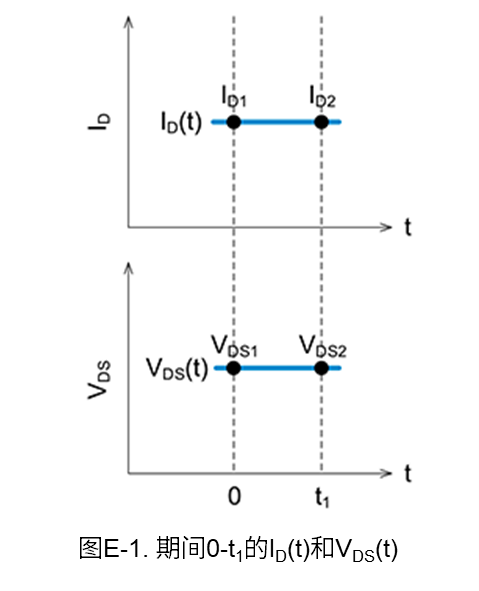
图E-1中0-t1期间的功率损耗\(P\),通常可以通过对公式(E-1)中的电流和电压之积进行积分来计算。
\(P = f \int_{0}^{t_1} I_D (t) V_{DS} (t) \, dt\) (E-1)
其中,\(f\):开关频率[Hz]
另外\(I_{D(t)}\)和\(V_{DS(t)}\)可根据图E-1中的斜率,用公式(E-2)和公式(E-3)来表示。
\(I_D\left(t\right)=I_{D1}\) (E-2)
\(V_{\mathrm{DS}}\left(t\right)=V_{\mathrm{DS1}}\) (E-3)
将公式(E-2)和公式(E-3)代入公式(E-1),
\(P = f \int_{0}^{t_1} I_{D1} V_{DS1} \, dt\) (E-4)
根据公式进行积分。
\(P=f\left[V_{\mathrm{DS1}}I_{D1}t\right]_0^{t_1}\) (E-5)
\(= V_{DS1} I_{D1} t_1 f \, [W]\) (E-6)
各种波形的开关损耗计算示例:例6:\(I_D\)恒定、\(V_{DS}\)下降波形(附录F)
下面我们根据开关波形的漏-源电压\(V_{DS}\)和漏极电流\(I_D\),使用线性近似方式计算开通时和关断时的功率损耗(开关损耗)。图F-1是用于损耗计算的波形。
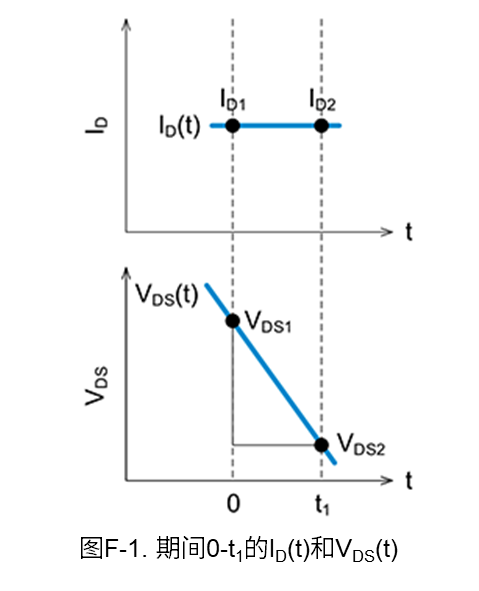
图F-1中0-t1期间的功率损耗\(P\),通常可以通过对公式(F-1)中的电流和电压之积进行积分来计算。
\(P = f \int_{0}^{t_1} I_D (t) V_{DS} (t) \, dt\) (F-1)
其中,\(f\):开关频率[Hz]
另外\(I_{D(t)}\)和\(V_{DS(t)}\)可根据图F-1中的斜率,用公式(F-2)和公式(F-3)来表示。
\(I_D\left(t\right)=I_{D1}\) (F-2)
\(V_{\mathrm{DS}}\left(t\right)=V_{\mathrm{DS1}}-\displaystyle \frac{V_{\mathrm{DS1}}-V_{\mathrm{DS2}}}{t_1}t\) (F-3)
将公式(F-2)和公式(F-3)代入公式(F-1),
\(P=f\int_{0}^{t_1}{I_{D1}\left(V_{\mathrm{DS1}}-\displaystyle \frac{V_{\mathrm{DS1}}-V_{\mathrm{DS2}}}{t_1}t\right)dt}\) (F-4)
\(=f\int_{0}^{t_1}\left(V_{\mathrm{DS1}}I_{D1}-\displaystyle \frac{I_{D1}\left(V_{\mathrm{DS1}}-V_{\mathrm{DS2}}\right)}{t_1}t\right)dt\) (F-5)
根据公式进行积分。
\(P=f\left[V_{\mathrm{DS1}}I_{D1}t-\displaystyle \frac{1}{2}\displaystyle \frac{I_{D1}\left(V_{\mathrm{DS1}}-V_{\mathrm{DS2}}\right)}{t_1}t^2\right]_0^{t_1}\) (F-6)
\(=f\left(V_{\mathrm{DS1}}I_{D1}t_1-\displaystyle \frac{1}{2}\displaystyle \frac{I_{D1}\left(V_{\mathrm{DS1}}-V_{\mathrm{DS2}}\right)}{t_1}t_1^2\right)\) (F-7)
\(=f\left(V_{\mathrm{DS1}}I_{D1}t_1-\displaystyle \frac{1}{2}\left(I_{D1}\left(V_{\mathrm{DS1}}-V_{\mathrm{DS2}}\right)\right)t_1\right)\) (F-8)
\(= \displaystyle \frac{1}{2} (V_{DS1} + V_{DS2}) I_{D1} t_1 f \, [W]\) (F-9)
求下列条件下的功率损耗。
・\(\underline{V_{DS2} ≔ 0}\) (F-10)
将公式(F-10)代入公式(F-9)。
\(P=\displaystyle \frac{1}{2}\left(V_{\mathrm{DS1}}+0\right)I_{D1}t_1f\) (F-11)
\(= \displaystyle \frac{1}{2} V_{DS1} I_{D1} t_1 f \, [W]\) (F-12)
各种波形的开关损耗计算示例:例7:\(I_D\)下降、\(V_{DS}\)上升波形(附录G)
下面我们根据开关波形的漏-源电压\(V_{DS}\)和漏极电流\(I_D\),使用线性近似方式计算开通时和关断时的功率损耗(开关损耗)。图G-1是用于损耗计算的波形。
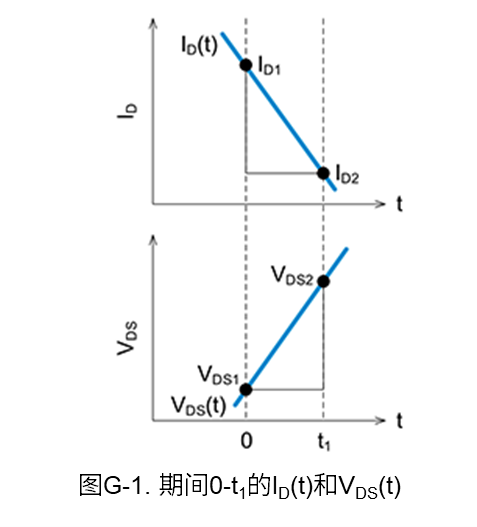
图G-1中0-t1期间的功率损耗\(P\),通常可以通过对公式(C-1)中的电流和电压之积进行积分来计算。
\(P = f \int_{0}^{t_1} I_D (t) V_{DS} (t) \, dt\) (G-1)
其中,\(f\):开关频率[Hz]
另外\(I_{D(t)}\)和\(V_{DS(t)}\)可根据图G-1中的斜率,用公式(G-2)和公式(G-3)来表示。
\(I_D\left(t\right)=I_{D1}-\displaystyle \frac{I_{D1}-I_{D2}}{t_1}\) (G-2)
\(V_{\mathrm{DS}}\left(t\right)=V_{\mathrm{DS1}}+\displaystyle \frac{V_{\mathrm{DS2}}-V_{\mathrm{DS1}}}{t_1}t=V_{\mathrm{DS1}}-\displaystyle \frac{V_{\mathrm{DS1}}-V_{\mathrm{DS2}}}{t_1}t\) (G-3)
将公式(G-2)和公式(G-3)代入公式(G-1),
\(P=f\int_{0}^{t_1}\left(I_{D1}-\displaystyle \frac{I_{D1}-I_{D2}}{t_1}t\right)\left(V_{\mathrm{DS1}}-\displaystyle \frac{V_{\mathrm{DS1}}-V_{\mathrm{DS2}}}{t_1}t\right)dt\) (G-4)
\(=f\int_{0}^{t_1}\left(V_{\mathrm{DS1}}I_{D1}-\displaystyle \frac{I_{D1}\left(V_{\mathrm{DS1}}-V_{\mathrm{DS2}}\right)}{t_1}t-\displaystyle \frac{V_{\mathrm{DS1}}\left(I_{D1}-I_{D2}\right)}{t_1}t+\displaystyle \frac{\left(V_{\mathrm{DS1}}-V_{\mathrm{DS2}}\right)\left(I_{D1}-I_{D2}\right)}{t_1^2}t^2\right)dt\) (G-5)
根据公式进行积分。
\(P=f\left[V_{\mathrm{DS1}}I_{D1}t-\displaystyle \frac{1}{2}\displaystyle \frac{I_{D1}\left(V_{\mathrm{DS1}}-V_{\mathrm{DS2}}\right)+V_{\mathrm{DS1}}\left(I_{D1}-I_{D2}\right)}{t_1}t^2+\displaystyle \frac{1}{3}\displaystyle \frac{\left(V_{\mathrm{DS1}}-V_{\mathrm{DS2}}\right)\left(I_{D1}-I_{D2}\right)}{t_1^2}t^3\right]_0^{t_1}\) (G-6)
\(=f\left[V_{\mathrm{DS1}}I_{D1}t_1-\displaystyle \frac{1}{2}\displaystyle \frac{I_{D1}\left(V_{\mathrm{DS1}}-V_{\mathrm{DS2}}\right)+V_{\mathrm{DS1}}\left(I_{D1}-I_{D2}\right)}{t_1}t_1^2+\displaystyle \frac{1}{3}\displaystyle \frac{\left(V_{\mathrm{DS1}}-V_{\mathrm{DS2}}\right)\left(I_{D1}-I_{D2}\right)}{t_1^2}t_1^3\right]\) (G-7)
\(=f\left[V_{\mathrm{DS1}}I_{D1}t_1-\displaystyle \frac{1}{2}\left(I_{D1}\left(V_{\mathrm{DS1}}-V_{\mathrm{DS2}}\right)+V_{\mathrm{DS1}}\left(I_{D1}-I_{D2}\right)\right)t_1+\displaystyle \frac{1}{3}\left(V_{\mathrm{DS1}}-V_{\mathrm{DS2}}\right)\left(I_{D1}-I_{D2}\right)t_1\right]\) (G-8)
\(= \left[ \displaystyle \frac{1}{3} (V_{DS1} – V_{DS2}) (I_{D1} – I_{D2}) – \displaystyle \frac{1}{2} I_{D1} (V_{DS1} – V_{DS2}) – \displaystyle \frac{1}{2} V_{DS1} (I_{D1} – I_{D2}) + V_{DS1} I_{D1} \right] t_1 f \, [W]\) (G-9)
求下列条件下的功率损耗。
・\(\underline{I_{DS2} ≔ 0}\) (G-10)
将公式(G-10)代入公式(G-9)。
\(P=\left[\displaystyle \frac{1}{3}\left(V_{\mathrm{DS1}}-V_{\mathrm{DS2}}\right)\left(I_{D1}-0\right)-\displaystyle \frac{1}{2}I_{D1}\left(V_{\mathrm{DS1}}-V_{\mathrm{DS2}}\right)-\displaystyle \frac{1}{2}V_{\mathrm{DS1}}\left(I_{D1}-0\right)+V_{\mathrm{DS1}}I_{D1}\right]t_1f\) (G-11)
\(=\left[\displaystyle \frac{1}{3}\left(V_{\mathrm{DS1}}-V_{\mathrm{DS2}}\right)I_{D1}-\displaystyle \frac{1}{2}I_{D1}\left(V_{\mathrm{DS1}}-V_{\mathrm{DS2}}\right)-\displaystyle \frac{1}{2}V_{\mathrm{DS1}}I_{D1}+V_{\mathrm{DS1}}I_{D1}\right]t_1f\) (G-12)
\(= \displaystyle \frac{1}{6} (2V_{DS1} + V_{DS2}) I_{D1} t_1 f \, [W]\) (G-13)
・\(\underline{V_{DS1}≔0}\) (G-14)
将公式(G-14)代入公式(G-9)。
\(P=\left[\displaystyle \frac{1}{3}\left(0-V_{\mathrm{DS2}}\right)\left(I_{D1}-I_{D2}\right)-\displaystyle \frac{1}{2}I_{D1}\left(0-V_{\mathrm{DS2}}\right)-\displaystyle \frac{1}{2}\times0\left(I_{D1}-I_{D2}\right)+0\times I_{D1}\right]t_1f\) (G-15)
\(=\left[-\displaystyle \frac{1}{3}V_{\mathrm{DS2}}\left(I_{D1}-I_{D2}\right)+\displaystyle \frac{1}{2}I_{D1}V_{\mathrm{DS2}}\right]t_1f\) (G-16)
\(= \displaystyle \frac{1}{6} V_{DS2} (I_{D1} + 2I_{D2}) t_1 f \, [W]\) (G-17)
・\(\underline{I_{D2} := 0, \quad V_{DS1} := 0}\) (G-18)
将公式(G-18)代入公式(G-9)。
\(P=\left[\displaystyle \frac{1}{3}\left(0-V_{\mathrm{DS2}}\right)\left(I_{D1}-0\right)-\displaystyle \frac{1}{2}I_{D1}\left(0-V_{\mathrm{DS2}}\right)-\displaystyle \frac{1}{2}\times0\left(I_{D1}-0\right)+0\times I_{D1}\right]t_1f\) (G-19)
\(=\left(-\displaystyle \frac{1}{3}V_{\mathrm{DS2}}I_{D1}+\displaystyle \frac{1}{2}I_{D1}V_{\mathrm{DS2}}\right)t_1f\) (G-20)
\(= \displaystyle \frac{1}{6} V_{DS2} I_{D1} t_1 f \, [W]\) (G-21)
各种波形的开关损耗计算示例:例8:\(I_D\)下降、\(V_{DS}\)恒定波形(附录H)
下面我们根据开关波形的漏-源电压\(V_{DS}\)和漏极电流\(I_D\),使用线性近似方式计算开通时和关断时的功率损耗(开关损耗)。图H-1是用于损耗计算的波形。
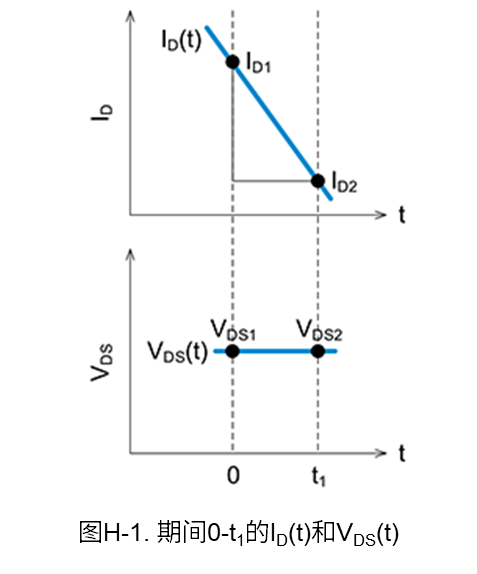
图H-1中0-t1期间的功率损耗\(P\),通常可以通过对公式(H-1)中的电流和电压之积进行积分来计算。
\(P = f \int_{0}^{t_1} I_D (t) V_{DS} (t) \, dt\) (H-1)
其中,\(f\):开关频率[Hz]
另外\(I_{D(t)}\)和\(V_{DS(t)}\)可根据图H-1中的斜率,用公式(H-2)和公式(H-3)来表示。
\(I_D\left(t\right)=I_{D1}-\displaystyle \frac{I_{D1}-I_{D2}}{t_1}t\) (H-2)
\(V_{DS}\left(t\right)=V_{DS1}\) (H-3)
将公式(H-2)和公式(H-3)代入公式(H-1),
\(P=f\int_{0}^{t_1}\left(I_{D1}-\displaystyle \frac{I_{D1}-I_{D2}}{t_1}t\right)\left(V_{DS1}\right)dt\) (H-4)
\(=f\int_{0}^{t_1}\left(V_{DS1}I_{D1}-\displaystyle \frac{V_{DS1}\left(I_{D1}-I_{D2}\right)}{t_1}t\right)dt\) (H-5)
根据公式进行积分。
\(P=f\left[V_{DS1}I_{D1}t-\displaystyle \frac{1}{2}\displaystyle \frac{V_{DS1}\left(I_{D1}-I_{D2}\right)}{t_1}t^2\right]_0^{t_1}\) (H-6)
\(=f\left[V_{DS1}I_{D1}t_1-\displaystyle \frac{1}{2}\displaystyle \frac{V_{DS1}\left(I_{D1}-I_{D2}\right)}{t_1}t_1^2\right]\) (H-7)
\(=f\left[V_{DS1}I_{D1}t_1-\displaystyle \frac{1}{2}\left(V_{DS1}\left(I_{D1}-I_{D2}\right)\right)t_1\right]\) (H-8)
\(= \displaystyle \frac{1}{2} V_{DS1} (I_{D1} + I_{D2}) t_1 f \, [W]\) (H-9)
求下列条件下的功率损耗。
・\(\underline{I_{D2} ≔ 0}\) (H-10)
将公式(H-10)代入公式(H-9)。
\(P = \displaystyle \frac{1}{2} V_{DS1} I_{D1} t_1 f \, [W]\) (H-11)
各种波形的开关损耗计算示例:例9:\(I_D\)下降、\(V_{DS}\)下降波形(附录I)
下面我们根据开关波形的漏-源电压\(V_{DS}\)和漏极电流\(I_D\),使用线性近似方式计算开通时和关断时的功率损耗(开关损耗)。图I-1是用于损耗计算的波形。
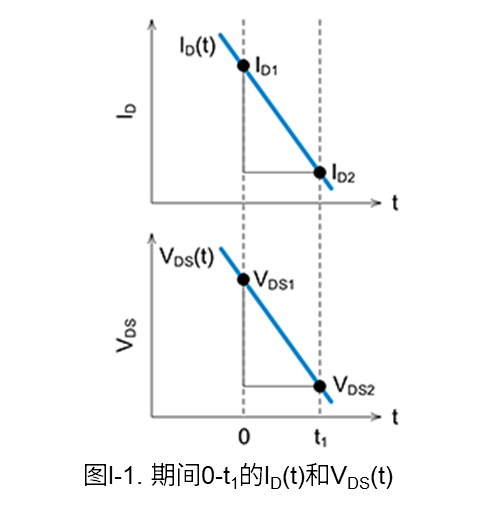
图I-1中0-t1期间的功率损耗\(P\),通常可以通过对公式(I-1)中的电流和电压之积进行积分来计算。
\(P = f \int_{0}^{t_1} I_D (t) V_{DS} (t) \, dt\) (I-1)
其中,\(f\):开关频率[Hz]
另外\(I_{D(t)}\)和\(V-{DS(t)}\)可根据图I-1中的斜率,用公式(I-2)和公式(I-3)来表示。
\(I_D\left(t\right)=I_{D1}-\displaystyle \frac{I_{D1}-I_{D2}}{t_1}t\) (I-2)
\(V_{DS}\left(t\right)=V_{DS1}-\displaystyle \frac{V_{DS1}-V_{DS2}}{t_1}t\) (I-3)
将公式(I-2)和公式(I-3)代入公式(I-1),
\(P=f\int_{0}^{t_1}\left(I_{D1}-\displaystyle \frac{I_{D1}-I_{D2}}{t_1}t\right)\left(V_{DS1}-\displaystyle \frac{V_{DS1}-V_{DS2}}{t_1}t\right)dt\) (I-4)
\(= f \int_{0}^{t_1} \left( V_{DS1} I_{D1} – \displaystyle \frac{I_{D1} (V_{DS1} – V_{DS2}) + V_{DS1} (I_{D1} – I_{D2})}{t_1} t + \displaystyle \frac{(V_{DS1} – V_{DS2}) (I_{D1} – I_{D2})}{t_1^2} t^2 \right) dt\) (I-5)
根据公式进行积分。
\(P=f\left[V_{DS1}I_{D1}t-\displaystyle \frac{1}{2}\displaystyle \frac{I_{D1}\left(V_{DS1}-V_{DS2}\right)+V_{DS1}\left(I_{D1}-I_{D2}\right)}{t_1}t^2+\displaystyle \frac{1}{3}\displaystyle \frac{\left(V_{DS1}-V_{DS2}\right)\left(I_{D1}-I_{D2}\right)}{t_1^2}t^3\right]_0^{t_1}\) (I-6)
\(=f\left[V_{DS1}I_{D1}t_1-\displaystyle \frac{1}{2}\displaystyle \frac{I_{D1}\left(V_{DS1}-V_{DS2}\right)+V_{DS1}\left(I_{D1}-I_{D2}\right)}{t_1}t_1^2+\displaystyle \frac{1}{3}\displaystyle \frac{\left(V_{DS1}-V_{DS2}\right)\left(I_{D1}-I_{D2}\right)}{t_1^2}t_1^3\right]\) (I-7)
\(=f\left[V_{DS1}I_{D1}t_1-\displaystyle \frac{1}{2}\left(I_{D1}\left(V_{DS1}-V_{DS2}\right)+V_{DS1}\left(I_{D1}-I_{D2}\right)\right)t_1+\displaystyle \frac{1}{3}\left(V_{DS1}-V_{DS2}\right)\left(I_{D1}-I_{D2}\right)t_1\right]\) (I-8)
\(=\left[\displaystyle \frac{1}{3}\left(V_{DS1}-V_{DS2}\right)\left(I_{D1}-I_{D2}\right)-\displaystyle \frac{1}{2}I_{D1}\left(V_{DS1}-V_{DS2}\right)-\displaystyle \frac{1}{2}V_{DS1}\left(I_{D1}-I_{D2}\right)+V_{DS1}I_{D1}\right]t_1f\ \left[W\right]\) (I-9)
求下列条件下的功率损耗。
・\(\underline{V_{DS2}≔0}\) (I-10)
将公式(I-10)代入公式(I-9)。
\(P=\left[\displaystyle \frac{1}{3}\left(V_{DS1}-0\right)\left(I_{D1}-I_{D2}\right)-\displaystyle \frac{1}{2}I_{D1}\left(V_{DS1}-0\right)-\displaystyle \frac{1}{2}V_{DS1}\left(I_{D1}-I_{D2}\right)+V_{DS1}I_{D1}\right]t_1f\) (I-11)
\(=\left[\displaystyle \frac{1}{3}V_{DS1}\left(I_{D1}-I_{D2}\right)-\displaystyle \frac{1}{2}I_{D1}V_{DS1}-\displaystyle \frac{1}{2}V_{DS1}\left(I_{D1}-I_{D2}\right)+V_{DS1}I_{D1}\right]t_1f\) (I-12)
\(= \displaystyle \frac{1}{6} V_{DS1} (2I_{D1} + I_{D2}) t_1 f \, [W]\) (I-13)
・\(\underline{I_{D2}≔0}\) (I-14)
将公式(I-14)代入公式(I-9)。
\(P=\left[\displaystyle \frac{1}{3}\left(V_{DS1}-V_{DS2}\right)\left(I_{D1}-0\right)-\displaystyle \frac{1}{2}I_{D1}\left(V_{DS1}-V_{DS2}\right)-\displaystyle \frac{1}{2}V_{DS1}\left(I_{D1}-0\right)+V_{DS1}I_{D1}\right]t_1f\) (I-15)
\(=\left[\displaystyle \frac{1}{3}\left(V_{DS1}-V_{DS2}\right)I_{D1}-\displaystyle \frac{1}{2}I_{D1}\left(V_{DS1}-V_{DS2}\right)-\displaystyle \frac{1}{2}V_{DS1}I_{D1}+V_{DS1}I_{D1}\right]t_1f\) (I-16)
\(= \displaystyle \frac{1}{6} (2V_{DS1} + V_{DS2}) I_{D1} t_1 f \, [W]\) (I-17)
各种波形的导通损耗计算示例
继“各种波形的开关损耗计算示例”之后,下面我们来看各种波形的导通损耗计算示例。我们将利用“通过波形的线性近似分割来计算损耗的方法”的表2中给出的所有基于线性近似分割计算导通损耗的公式,来计算1~3种情况(附录J~L)下的导通损耗。
各种波形的导通损耗计算示例
- 例1:\(I_D\)上升波形(附录J)
- 例2:\(I_D\)恒定波形(附录K)
- 例3:\(I_D\)下降波形(附录L)
各种波形的导通损耗计算示例:例1:ID上升波形(附录J)
我们通过MOSFET的导通电阻\(R_{ON}\)和开关波形中的漏极电流\(I_D\),利用线性近似法来求导通期间(0-t1)的功率损耗。图J-1是用于损耗计算的波形。
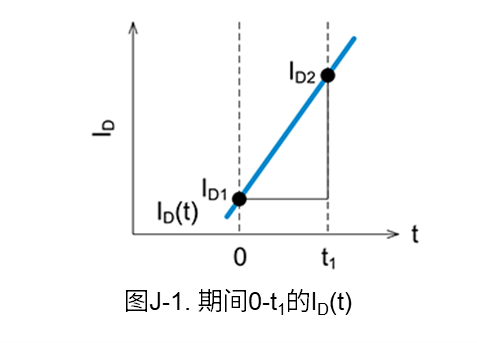
在图J-1中,由于在0-t10期间MOSFET处于导通状态,因此\(V_{DS}\)等于MOSFET的导通电阻\(R_{ON}\)与\(I_D\)的乘积。
在0-t1期间的功率损耗\(P\),通常可以通过公式(J-1)中的电阻与电流平方的乘积积分进行计算。
\(P = f \int_{0}^{t_1} R_{ON} I_D (t)^2 \, dt\) (J-1)
其中,\(R_{ON}\):MOSFET的导通电阻[Ω]
\(f\):开关频率[Hz]
另外,\(I_{D(t)}\)可根据图J-1中的斜率,用公式(J-2)来表示。
\(I_D\left(t\right)=I_{D1}+\displaystyle \frac{I_{D2}-I_{D1}}{t_1}t=I_{D1}-\displaystyle \frac{I_{D1}-I_{D2}}{t_1}t\) (J-2)
将公式(J-2)代入公式(J-1)。
\(P=f\int_{0}^{t_1}{R_{\mathrm{ON}}\left(I_{D1}-\displaystyle \frac{I_{D1}-I_{D2}}{t_1}t\right)^2dt}\) (J-3)
\(=f\int_{0}^{t_1}{R_{\mathrm{ON}}\left(I_{D1}^2-2I_{D1}\displaystyle \frac{I_{D1}-I_{D2}}{t_1}t+\displaystyle \frac{\left(I_{D1}-I_{D2}\right)^2}{t_1^2}t^2\right)dt}\) (J-4)
根据公式进行积分。
\(P=fR_{\mathrm{ON}}\left[I_{D1}^2-2I_{D1}\displaystyle \frac{I_{D1}-I_{D2}}{2t_1}t^2+\displaystyle \frac{\left(I_{D1}-I_{D2}\right)^2}{3t_1^2}t^3\right]_0^{t_1}\) (J-5)
\(=fR_{\mathrm{ON}}\left(I_{D1}^2t_1-2I_{D1}\displaystyle \frac{I_{D1}-I_{D2}}{2t_1}t_1^2+\displaystyle \frac{\left(I_{D1}-I_{D2}\right)^2}{3t_1^2}t_1^3\right)\) (J-6)
\(P=fR_{\mathrm{ON}}\left(I_{D1}^2t_1-I_{D1}\left(I_{D1}-I_{D2}\right)t_1+\displaystyle \frac{\left(I_{D1}-I_{D2}\right)^2}{3}t_1\right)\) (J-7)
\(=fR_{\mathrm{ON}}\left(I_{D1}^2-I_{D1}\left(I_{D1}-I_{D2}\right)+\displaystyle \frac{\left(I_{D1}-I_{D2}\right)^2}{3}\right)t_1\) (J-8)
\(=fR_{\mathrm{ON}}\left(I_{D1}I_{D2}+\displaystyle \frac{I_{D1}^2-2I_{D1}I_{D2}+I_{D2}^2}{3}\right)t_1\) (J-9)
\(=fR_{\mathrm{ON}}\left(\displaystyle \frac{I_{D1}^2-2I_{D1}I_{D2}+I_{D2}^2-3I_{D1}^2+3I_{D1}I_{D2}+3I_{D1}^2}{3}\right)t_1\) (J-10)
\(= \displaystyle \frac{1}{3} R_{ON} (I_{D1}^2 + I_{D1} I_{D2} + I_{D2}^2) t_1 f \, [W]\) (J-11)
SiC MOSFET:各种波形的导通损耗计算示例:例2:\(I_D\)恒定波形(附录K)
我们通过MOSFET的导通电阻\(R_{ON}\)和开关波形中的漏极电流\(I_D\),利用线性近似法来求导通期间(0-t1)的功率损耗。图K-1是用于损耗计算的波形。
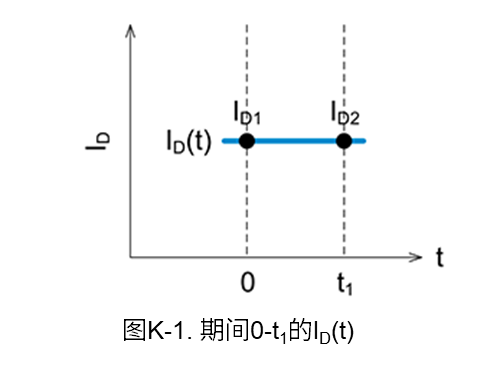
在图K-1中,由于在0-t10期间MOSFET处于导通状态,因此\(V_{DS}\)等于MOSFET的导通电阻\(R_{ON}\)与\(I_D\)的乘积。
在0-t1期间的功率损耗\(P\),通常可以通过公式(K-1)中的电阻与电流平方的乘积积分进行计算。
\(P = f \int_{0}^{t_1} R_{ON} I_D (t)^2 \, dt\) (K-1)
其中,\(R_{ON}\):MOSFET的导通电阻[Ω]
\(f\):开关频率[Hz]
另外,\(I_{D(t)}\)可根据图K-1中的斜率,用公式(K-2)来表示。
\(I_D\left(t\right)=I_{D1}\) (K-2)
将公式(K-2)代入公式(K-1)。
\(P = f \int_{0}^{t_1} R_{ON} I_{D1}^2 \, dt\) (K-3)
根据公式进行积分。
\(P=f\left[R_{ON} I_{D1}^2\right]_0^{t_1}\) (K-4)
\(P= R_{ON} I_{D1}^2 t_1 f \, [W]\) (K-5)
SiC MOSFET:各种波形的导通损耗计算示例:例3:\(I_D\)下降波形(附录L)
我们通过MOSFET的导通电阻\(R_{ON}\)和开关波形中的漏极电流\(I_D\),利用线性近似法来求导通期间(0-t1)的功率损耗。图L-1是用于损耗计算的波形。
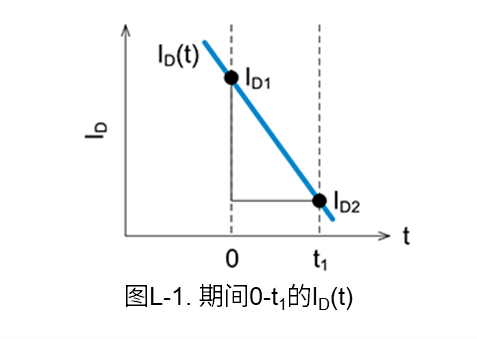
在图L-1中,由于在0-t10期间MOSFET处于导通状态,因此\(V_{DS}\)等于MOSFET的导通电阻\(R_{ON}\)与\(I_D\)的乘积。
在0-t1期间的功率损耗\(P\),通常可以通过公式(L-1)中的电阻与电流平方的乘积积分进行计算。
\(P = f \int_{0}^{t_1} R_{ON} I_D (t)^2 \, dt\) (L-1)
其中,\(R_{ON}\):MOSFET的导通电阻[Ω]
\(f\):开关频率[Hz]
另外,\(I_{D(t)}\)可根据图L-1中的斜率,用公式(L-2)来表示。
\(I_D\left(t\right)=I_{D1}-\displaystyle \frac{I_{D1}-I_{D2}}{t_1}t\) (L-2)
将公式(L-2)代入公式(L-1)。
\(P=f\int_{0}^{t_1}{R_{\mathrm{ON}}\left(I_{D1}-\displaystyle \frac{I_{D1}-I_{D2}}{t_1}\right)^2dt}\) (L-3)
\(=f\int_{0}^{t_1}{R_{\mathrm{ON}}\left({I_{D1}}^2-2I_{D1}\displaystyle \frac{I_{D1}-I_{D2}}{t_1}t+\displaystyle \frac{\left(I_{D1}-I_{D2}\right)^2}{{t_1}^2}t^2\right)dt}\) (L-4)
根据公式进行积分。
\(P=fR_{\mathrm{ON}}\left[{I_{D1}}^2-2I_{D1}\displaystyle \frac{I_{D1}-I_{D2}}{2t_1}t^2+\displaystyle \frac{\left(I_{D1}-I_{D2}\right)^2}{3t_1^2}t^3\right]_0^{t_1}\) (L-5)
\(=fR_{\mathrm{ON}}\left({I_{D1}}^2t_1-2I_{D1}\displaystyle \frac{I_{D1}-I_{D2}}{2t_1}t_1^2+\displaystyle \frac{\left(I_{D1}-I_{D2}\right)^2}{3{t_1}^2}t_1^3\right)\) (L-6)
\(=fR_{\mathrm{ON}}\left({I_{D1}}^2t_1-I_{D1}\left(I_{D1}-I_{D2}\right)t_1+\displaystyle \frac{\left(I_{D1}-I_{D2}\right)^2}{3}t_1\right)\) (L-7)
\(=fR_{\mathrm{ON}}\left({I_{D1}}^2-I_{D1}\left(I_{D1}-I_{D2}\right)+\displaystyle \frac{\left(I_{D1}-I_{D2}\right)^2}{3}\right)t_1\) (L-8)
\(=fR_{\mathrm{ON}}\left(I_{D1}I_{D2}+\displaystyle \frac{{I_{D1}}^2-2I_{D1}I_{D2}+{I_{D2}}^2}{3}\right)t_1\) (L-9)
\(=fR_{\mathrm{ON}}\left(\displaystyle \frac{{I_{D1}}^2-2I_{D1}I_{D2}+{I_{D2}}^2-3I_{D1}^2+3I_{D1}I_{D2}+3I_{D1}^2}{3}\right)t_1\) (L-10)
\(= \displaystyle \frac{1}{3} R_{ON} (I_{D1}^{\hspace{0.5em} 2} + I_{D1} I_{D2} + I_{D2}^{\hspace{0.5em} 2}) t_1 f \, [W]\) (L-11)