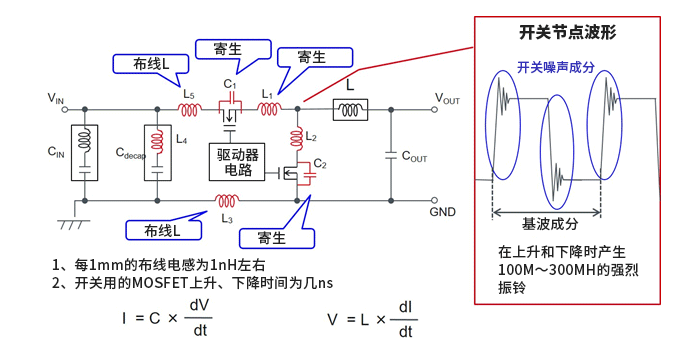
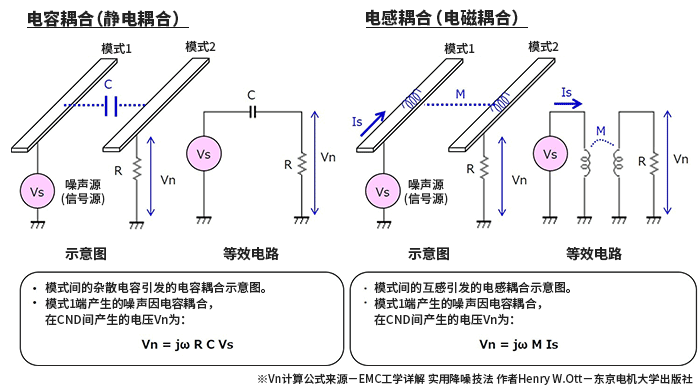
上一篇以“何谓EMC”为题对EMC的基础–EMC相关的术语意义进行了解说。本文将介绍“频谱基础”。
作为基础内容,先简单介绍一下“何谓频谱?”。根据日文版“大英百科全书 小项目版(支持电子版)”的解释,“将电磁波分解为正弦波分量,并按波长顺序排列的波谱”,将该释义扩展开来就是“将具有复杂组成的东西分解为单纯成分,并把这些成分按其特征量的大小依序排列(部分省略)”。虽然所引用的解释比较简短,不过再次仔细思考就会觉得“的确如此”。
这里介绍的频谱是指电气信号的频谱。具体来说,是基于通称“频谱分析仪/Spectrum Analyzer”的频谱分析仪器的数据(横轴作为频率,纵轴作为功率或电压)进行介绍。
频谱基础
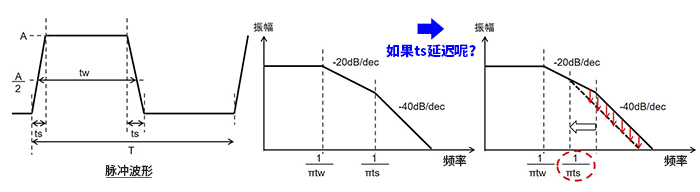
本文的主题是“开关电源的EMC”,因此电气信号是以开关信号为前提的。首先来看下面的原理示意图。在表示开关信号的脉冲波形中,包括tw(脉冲宽度)和ts(上升/下降时间)。
中间的图是基于傅里叶变换的理论上的脉冲波形频谱。这是“振幅随着频率的升高而衰减,衰减斜率随着tw和ts而变化”的常见频谱。
右图表示脉冲的ts延迟后的频谱变化。斜率变为-40dB/dec时的1/πts频率降低是理所当然的,最终结果是其后的振幅减少。简而言之就是“当ts延迟时频谱的振幅衰减”。
接下来将使用实际的频谱分析仪数据来看频率等其他参数变化时的频谱变化。这里的关键点是“对于信号波形的变化,频谱将以怎样的趋势变化”。这是用来通过实际的开关电源电路的开关相关的频谱来分析并解决EMC问题所必须的知识。
波形变化与频谱变化
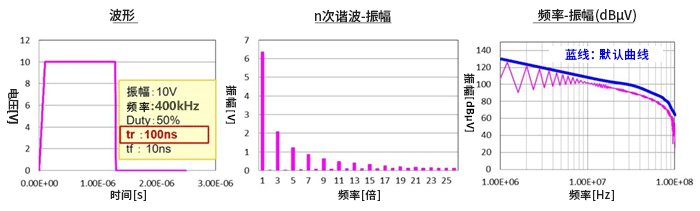
前面给出的图是用来比较的默认条件下的数据。下面波形图中的条件是:振幅10V,频率400kHz,Duty(占空比)50%,tr/tf(上升时间/下降时间)10ns。
中间的图表示n次谐波和振幅(V)的关系。1倍的频率=基波,也就是说400kHz的分量最大,以奇数倍的频率形成频谱。
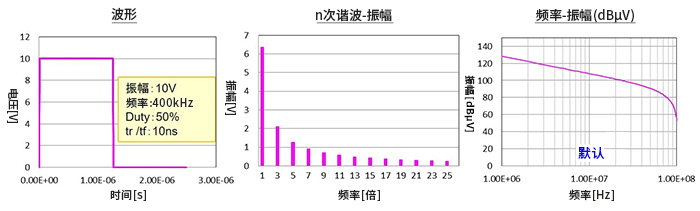
谐波仅为奇数次是Duty为50%=1:1的频谱特征。各分量的大小为基波分量的1/次数,例如3次谐波分量为1/3,n次谐波分量为1/n。
右图是振幅为dBµV的对数曲线图。顺便提一下,dBμV是基于以1µV电压为基准的电压比的dB值。
①将频率变更为2MHz时的频谱。从频率-振幅(dBµV)关系图可以明确看出,当频率增加时振幅整体增加。
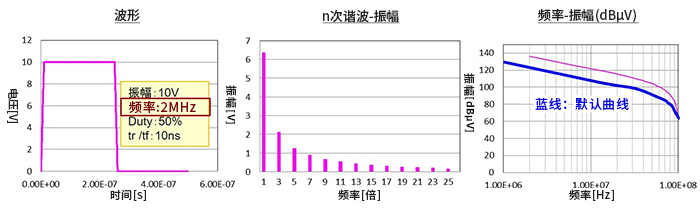
②tr和tf同时延迟为100ns时的频谱。结果如原理示意图所示,进入-40dB/dec衰减时的频率降低,频谱的振幅衰减。
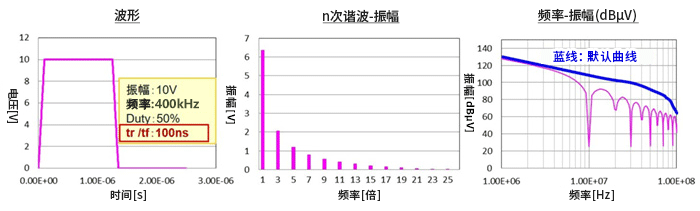
③将Duty50%变为20%时的频谱。由于Duty不是1:1,因此会产生偶次谐波,但峰值基本上没变化。随着脉冲宽度tw变窄,基波频谱的振幅衰减。
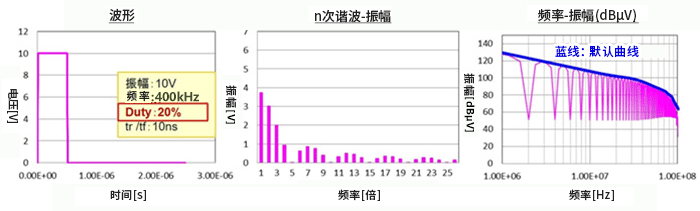
④仅tr(上升时间)延迟时的频普。tr相关的分量因tr延迟而从更低的频率开始衰减。
下面汇总了每种情况的结果。总而言之,当频率较低且上升/下降较慢时,频谱会衰减。从EMC的角度来看,也就是频谱的振幅较低时更有利。
- ①频率升高
- ②上升/下降延迟
- ③Duty变更
- ④仅上升延迟
- ⇒ 频谱的振幅整体増加
- ⇒ 进入-40dB/dec衰减时的频率变低,频谱的振幅衰减
- ⇒ 产生偶次谐波,但对谱峰无影响。
基波频谱衰减 - ⇒ tr分量从更低的频率开始衰减
另外,这里的“频谱”是指英语的“Spectrum”。虽然这并非本文主题,但稍微介绍一下仅作为了解。
下次计划介绍“差模噪声与共模噪声”。